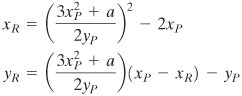Section 10.3. Elliptic Curve Arithmetic

[Page 301 (continued)]

10.3. Elliptic Curve Arithmetic

Most of the products and standards that use public-key cryptography for encryption and digital signatures use RSA. As we have seen, the key length for secure RSA use has increased over recent years, and this has put a heavier processing load on applications using RSA. This burden has ramifications, especially for electronic commerce sites that conduct large numbers of secure transactions. Recently, a competing system has begun to challenge RSA: elliptic curve cryptography (ECC). Already, ECC is showing up in standardization efforts, including the IEEE P1363 Standard for Public-Key Cryptography.

[Page 302]

The principal attraction of ECC, compared to RSA, is that it appears to offer equal security for a far smaller key size, thereby reducing processing overhead. On the other hand, although the theory of ECC has been around for some time, it is only recently that products have begun to appear and that there has been sustained cryptanalytic interest in probing for weaknesses. Accordingly, the confidence level in ECC is not yet as high as that in RSA.

ECC is fundamentally more difficult to explain than either RSA or Diffie-Hellman, and a full mathematical description is beyond the scope of this book. This section and the next give some background on elliptic curves and ECC. We begin with a brief review of the concept of abelian group. Next, we examine the concept of elliptic curves defined over the real numbers. This is followed by a look at elliptic curves defined over finite fields. Finally, we are able to examine elliptic curve ciphers.

The reader may wish to review the material on finite fields in Chapter 4 before proceeding.

Abelian Groups

Recall from Chapter 4, that an abelian group G, sometimes denoted by {G, • }, is a set of elements with a binary operation, denoted by •, that associates to each ordered pair (a, b) of elements in G an element (a • b) in G, such that the following axioms are obeyed:^[2]

^[2] The operator • is generic and can refer to addition, multiplication, or some other mathematical operation.

(A1) Closure:	If a and b belong to G, then a • b is also in G.
(A2) Associative:	a • (b • c) = (a • b) • c for all a, b, c in G.
(A3) Identity element:	There is an element e in G such that a • e = e • a = a for all a in G.
(A4) Inverse element:	For each a in G there is an element a' in G such that a • a' = a' • a = e.
(A5) Commutative:	a • b = b • a for all a, b in G.

A number of public-key ciphers are based on the use of an abelian group. For example, Diffie-Hellman key exchange involves multiplying pairs of nonzero integers modulo a prime number q. Keys are generated by exponentiation over the group, with exponentiation defined as repeated multiplication. For example, a^k mod q = mod q. To attack Diffie-Hellman, the attacker must determine k given a and a^k; this is the discrete log problem.

For elliptic curve cryptography, an operation over elliptic curves, called addition, is used. Multiplication is defined by repeated addition. For example, , where the addition is performed over an elliptic

curve. Cryptanalysis involves determining k given a and (a x k).

[Page 303]

An elliptic curve is defined by an equation in two variables, with coefficients. For cryptography, the variables and coefficients are restricted to elements in a finite field, which results in the definition of a finite abelian group. Before looking at this, we first look at elliptic curves in which the variables and coefficients are real numbers. This case is perhaps easier to visualize.

Elliptic Curves over Real Numbers

Elliptic curves are not ellipses. They are so named because they are described by cubic equations, similar to those used for calculating the circumference of an ellipse. In general, cubic equations for elliptic curves take the form

y² + axy + by = x³ + cx² + dx + e

where a, b, c, d, and e are real numbers and x and y take on values in the real numbers.^[3] For our purpose, it is sufficient to limit ourselves to equations of the form

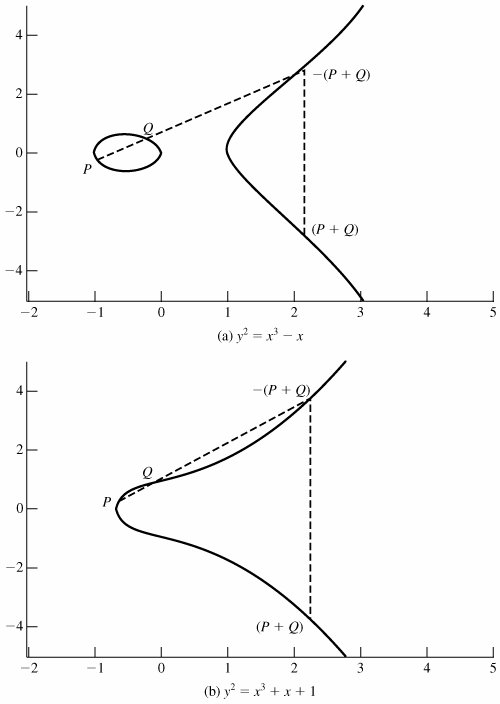
^[3] Note that x and y are true variables, which take on values. This is in contrast to our discussion of polynomial rings and fields in Chapter 4, where x was treated as an indeterminate.

Equation 10-1

Such equations are said to be cubic, or of degree 3, because the highest exponent they contain is a 3. Also included in the definition of an elliptic curve is a single element denoted O and called the point at infinity or the zero point, which we discuss subsequently. To plot such a curve, we need to compute

For given values of a and b, the plot consists of positive and negative values of y for each value of x. Thus each curve is symmetric about y = 0. Figure 10.9 shows two examples of elliptic curves. As you can see, the formula sometimes produces weird-looking curves.

Figure 10.9. Example of Elliptic Curves (This item is displayed on page 304 in the print version)

Now, consider the set of points E(a, b) consisting of all of the points (x, y) that satisfy Equation (10.1) together with the element O. Using a different value of the pair (a, b) results in a different set E(a, b). Using this terminology, the two curves in Figure 10.9 depict the sets E(1,0) and E(1, 1), respectively.

Geometric Description of Addition

It can be shown that a group can be defined based on the set E(a, b) for specific values of a and b in Equation (10.1), provided the following condition is met:

Equation 10-2

To define the group, we must define an operation, called addition and denoted by +, for the set E(a, b), where a and b satisfy Equation (10.2). In geometric terms, the rules for addition can be stated as follows: If three points on an elliptic curve lie on a straight line, their sum is O. From this definition, we can define the rules of addition over an elliptic curve:

O serves as the additive identity. Thus O = O; for any point P on the elliptic curve, P + O = P. In what follows, we assume P Q
[Page 304]
The negative of a point P is the point with the same x coordinate but the negative of the y coordinate; that is, if P = (x, y), then P = (x, y). Note that these two points can be joined by a vertical line. Note that P + (P) = P P = O.
To add two points P and Q with different x coordinates, draw a straight line between them and find the third point of intersection R. It is easily seen that there is a unique point R that is the point of intersection (unless the line is tangent to the curve at either P or Q, in which case we take R = P or R = Q, respectively). To form a group structure, we need to define addition on these three points as follows: P + Q = R. That is, we define P + Q to be the mirror image (with respect to the x axis) of the third point of intersection. Figure 10.9 illustrates this construction.

[Page 305]

The geometric interpretation of the preceding item also applies to two points, P and P, with the same x coordinate. The points are joined by a vertical line, which can be viewed as also intersecting the curve at the infinity point. We therefore have P + ( P) = O, consistent with item (2).
To double a point Q, draw the tangent line and find the other point of intersection S. Then Q + Q = 2Q = S.

With the preceding list of rules, it can be shown that the set E(a, b) is an abelian group.

Algebraic Description of Addition

In this subsection we present some results that enable calculation of additions over elliptic curves.^[4] For two distinct points P = (x_P, y_P) and Q = (x_Q, y_Q) that are not negatives of each other, the slope of the line l that joins them is D = (y_Q y_P). There is exactly one other point where l intersects the elliptic curve, and that is the negative of the sum of P and Q. After some algebraic manipulation, we can express the sum R = P + Q as follows:

^[4] For derivations of these results, see [KOBL94] or other mathematical treatments of elliptic curves.

Equation 10-3

We also need to be able to add a point to itself: P + P = 2P = R. When y_P 0, the expressions are

Equation 10-4

Elliptic Curves over Z_p

Elliptic curve cryptography makes use of elliptic curves in which the variables and coefficients are all restricted to elements of a finite field. Two families of elliptic curves are used in cryptographic applications: prime curves over Z_p and binary curves over GF(2^m). For a prime curve over Z_p, we use a cubic equation in which the variables and coefficients all take on values in the set of integers from 0 through p 1 and in which calculations are performed modulo p. For a binary curve defined over GF(2^m), the variables and coefficients all take on values in GF(2ⁿ) and in calculations are performed over GF(2ⁿ). [FERN99] points out that prime curves are best for software applications, because the extended bit-fiddling operations needed by binary curves are not required; and that binary curves are best for hardware applications, where it takes remarkably few logic gates to create a powerful, fast cryptosystem. We examine these two families in this section and the next.

There is no obvious geometric interpretation of elliptic curve arithmetic over finite fields. The algebraic interpretation used for elliptic curve arithmetic over real numbers does readily carry over, and this is the approach we take.

[Page 306]

For elliptic curves over Z_p, as with real numbers, we limit ourselves to equations of the form of Equation (10.1), but in this case with coefficients and variables limited to Z_p:

Equation 10-5

For example, Equation (10.5) is satisfied for a = 1, b = 1, x = 9, y = 9, y = 7, p = 23:

7² mod 23	= (9³ + 9 + 1) mod 23
49 mod 23	= 739 mod 23
3	= 3

Now consider the set E_p (a, b) consisting of all pairs of integers (x, y) that satisfy Equation (10.5), together with a point at infinity O. The coefficients a and b and the variables x and y are all elements of Z_p.

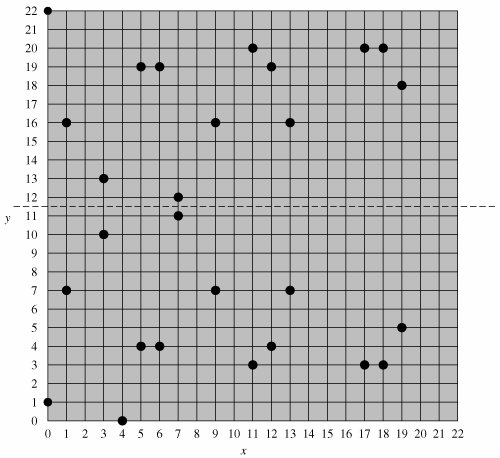
For example, let p = 23 and consider the elliptic curve y² = x³ + x + 1. In this case, a = b = 1. Note that this equation is the same as that of Figure 10.9b. The figure shows a continuous curve with all of the real points that satisfy the equation. For the set E₂₃(1, 1), we are only interested in the nonnegative integers in the quadrant from (0, 0) through (p 1, p 1) that satisfy the equation mod p. Table 10.1 lists the points (other than O) that are part of E₂₃(1,1). Figure 10.10 plots the points of E₂₃(1,1); note that the points, with one exception, are symmetric about y = 11.5.

Table 10.1. Points on the Elliptic Curve E₂₃(1,1)
(0, 1)	(6, 4)	(12, 19)
(0, 22)	(6, 19)	(13, 7)
(1, 7)	(7, 11)	(13, 16)
(1, 16)	(7, 12)	(17, 3)
(3, 10)	(9, 7)	(17, 20)
(3, 13)	(9, 16)	(18, 3)
(4, 0)	(11, 3)	(18, 20)
(5, 4)	(11, 20)	(19, 5)
(5, 19)	(12, 4)	(19, 18)

Figure 10.10. The Elliptic Curve E₂₃(1,1) (This item is displayed on page 307 in the print version)

It can be shown that a finite abelian group can be defined based on the set E_p(a, b) provided that (x³ + ax + b) mod p has no repeated factors. This is equivalent to the condition

Equation 10-6

Note that Equation (10.6) has the same form as Equation (10.2).

The rules for addition over E_p(a, b) correspond to the algebraic technique described for elliptic curves defined over real number. For all points P, Q Ea, b);

P + O = P.
If P = (x_P, y_P) then P + (x_P, y_P) = O. The point (x_P, y_P) is the negative of P, denoted as P. For example, in E₂₃(1,1), for P = (13,7), we have P = (13, 7). But 7 mod 23 = 16. Therefore, P = (13, 16), which is also in E₂₃(1,1).

[Page 307]

If P = (x_P, y_Q) and Q = (x_Q, y_Q) with P R = P + Q = (x_R, y_R) is determined by the following rules:
x_R = (l² x_P x_Q) mod p
y_R = (l(x_P x_R) y_P) mod p
where
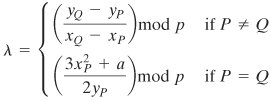
Multiplication is defined as repeated addition; for example, 4P = P + P + P + P.
For example, let P = (3,10) and Q = (9,7) in E₂₃(1,1). Then

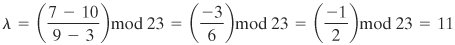
x_R = (11² 3 9) mod 23 = 17
y_R = (11(3 17) 10) mod 23 = 164 mod 23 = 20

[Page 308]

So P + Q = (17, 20). To find 2P,

The last step in the preceding equation involves taking the multiplicative inverse of 4 in Z₂₃. This can be done using the extended Euclidean algorithm defined in Section 4.4. To confirm, note that (6 x 4) mod 23 = 24 mod 23 = 1.

x_R = (6² 3 3) mod 23 = 30 mod 23 = 7

y_R = (6(3 7) 10) mod 23 = ( 34) mod 23 = 12

and 2P = (7, 12).

For determining the security of various elliptic curve ciphers, it is of some interest to know the number the number of points in a finite abelian group defined over an elliptic curve. In the case of the finite group E_p(a,b), the number of points N is bounded by

Note that the number of points in E_p(a, b) is approximately equal to the number of elements in Zp, namely p elements.

Elliptic Curves over GF(2^m)

Recall from Chapter 4 that a finite field GF(2^m) consists of 2^m elements, together with addition and multiplication operations that can be defined over polynomials. For elliptic curves over GF(2^m), we use a cubic equation in which the variables and coefficients all take on values in GF(2^m), for some number m, and in which calculations are performed using the rules of arithmetic in GF(2^m).

It turns out that the form of cubic equation appropriate for cryptographic applications for elliptic curves is somewhat different for GF(2^m) than for Z_p. The form is

Equation 10-7

where it is understood that the variables x and y and the coefficients a and b are elements of GF(2^m) of and that calculations are performed in GF(2^m).

Now consider the set E_2^m(a, b) consisting of all pairs of integers (x, y) that satisfy Equation (10.7), together with a point at infinity O.

For example, let us use the finite field GF(2⁴) with the irreducible polynomial f(x) = x⁴ + x + 1. This yields a generator that satisfies f(g) = 0, with a value of g⁴ = g + 1, or in binary 0010. We can develop the powers of g as follows:

g⁰ = 0001	g⁴ = 0011	g⁸ = 0101	g¹² = 1111
g¹ = 0010	g⁵ = 0110	g⁹ = 1010	g¹³ = 1101
g² = 0100	g⁶ = 1100	g¹⁰ = 0111	g¹⁴ = 1001
g³ = 1000	g⁷ = 1011	g¹¹ = 1110	g¹⁵ = 0001

For example, g⁵ = (g⁴)(g) = g² + g = 0110.

[Page 309]

Now consider the elliptic curve y² + xy = x³ + g⁴x² + 1. In this case a = g⁴ and b = g⁰ = 1. One point that satisfies this equation is (g⁵, g³):

(g³)² + (g⁵)(g³) = (g⁵)³ + (g⁴)(g⁵)² + 1

g⁶ + g⁸ = g¹⁵ + g¹⁴ + 1

1100 + 0101 = 0001 + 1001 + 0001

1001 = 1001

Table 10.2 lists the points (other than O) that are part of E_2⁴(g⁴, 1). Figure 10.11 plots the points of E_2⁴(g⁴, 1).

Table 10.2. Points on the Elliptic Curve E_2⁴ (g⁴, 1)
(0, 1)	(g⁵, g³)	(g⁹, g¹³)
(1, g⁶)	(g⁵, g¹¹)	(g¹⁰, g)
(1, g¹³)	g⁶, g⁸)	(g¹⁰, g⁸)
(g³, g⁸)	(g⁶, g¹⁴)	(g¹²,0)
(g³, g¹³)	(g⁹, g¹⁰)	(g¹², g¹²)

Figure 10.11. The Elliptic Curve E_2⁴(g⁴, 1)

It can be shown that a finite abelian group can be defined based on the set E_2m(a, b), provided that b 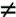0. The rules for addition can be stated as follows. For all points Q 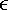E_{2^{a, b):}}

P + O = P.
If P = (x_P, y_P), then P + (x_P, x_p + y_P) = O. The point (x_P, x_P + y_P) is the negative of P, denoted as P.

[Page 310]

If P = (x_P, y_P) and Q = (x_Q, y_Q) with 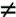P P 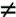R = P + Q = (x_R, y_R) is determined by the following rules:
x_R = l² + l + x_P + x_Q + a
y_R = l(x_P + x_R) + x_R + y_P
where
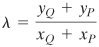
If = (x_P, y_P) then R = 2P = (x_R, y_R) is determined by the following rules:

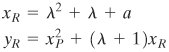
where