Multiplicative inverse (w1) | For each w  Zw Zw  0, there exists a 0, there exists a
Zw x z  1 (mod Because w is relatively prime to p, if we multiply all the elements of Zp by w, the resulting residues are all of the elements of Zp permuted. Thus, exactly one of the residues has the value 1. Therefore, there is some integer Zp in that, when multiplied by w, yields the residue 1. That integer is the multiplicative inverse of w, designated w1. Therefore, Zp is in fact a finite field. Further, Equation (4.3) is consistent with the existence of a multiplicative inverse and can be rewritten without the condition: 1 (mod Because w is relatively prime to p, if we multiply all the elements of Zp by w, the resulting residues are all of the elements of Zp permuted. Thus, exactly one of the residues has the value 1. Therefore, there is some integer Zp in that, when multiplied by w, yields the residue 1. That integer is the multiplicative inverse of w, designated w1. Therefore, Zp is in fact a finite field. Further, Equation (4.3) is consistent with the existence of a multiplicative inverse and can be rewritten without the condition: Equation 4-5 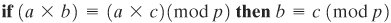
Multiplying both sides of Equation (4.5) by the multiplicative inverse of a, we have: ((a1) x a x b) |  ((a x c)(mod p) ((a x c)(mod p)
| b |  p) p)
|
| The simplest finite field is GF(2). Its arithmetic operations are easily summarized: 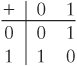
| 
| 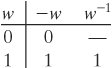
| Addition | Multiplication | Inverses |
In this case, addition is equivalent to the exclusive-OR (XOR) operation, and multiplication is equivalent to the logical AND operation. |
| Table 4.3 shows GF(7). This is a field of order 7 using modular arithmetic modulo 7. As can be seen, it satisfies all of the properties required of a field (Figure 4.1). Compare this table with Table 4.1. In the latter case, we see that the set Z8 using modular arithmetic modulo 8, is not a field. Later in this chapter, we show how to define addition and multiplication operations on Z8 in such a way as to form a finite field. Table 4.3. Arithmetic in GF(7) (This item is displayed on page 111 in the print version) 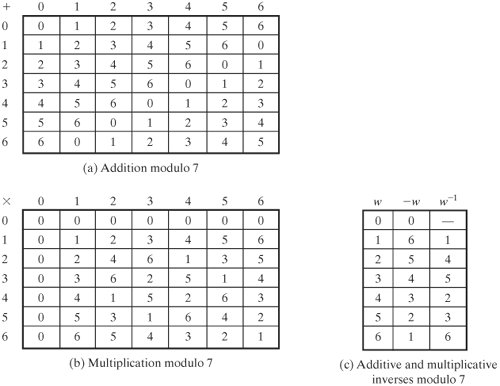
|
Finding the Multiplicative Inverse in GF(p) It is easy to find the multiplicative inverse of an element in GF(p) for small values of p. You simply construct a multiplication table, such as shown in Table 4.3b, and the desired result can be read directly. However, for large values of p, this approach is not practical. If gcd(m, b) = 1, then b has a multiplicative inverse modulo m. That is, for positive integer b < m, there exists a b1 < m such that bb1 = 1 mod m. The Euclidean algorithm can be extended so that, in addition to finding gcd(m, b), if the gcd is 1, the algorithm returns the multiplicative inverse of b.
[Page 111]EXTENDED EUCLID(m, b) 1. (A1, A2, A3)  (1, 0, (0, 1, 2. if B3 = 0 return A3 = gcd(m, b); no inverse 3. if B3 = 1 return B3 = gcd(m, b); B2 = b1 mod m (1, 0, (0, 1, 2. if B3 = 0 return A3 = gcd(m, b); no inverse 3. if B3 = 1 return B3 = gcd(m, b); B2 = b1 mod m
4. 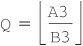 5. (T1, T2, T3)  (A1 QB1, A2 QB2, A3 QB3) 6. (A1, A2, A3) (A1 QB1, A2 QB2, A3 QB3) 6. (A1, A2, A3)  (B1, B2, B3) 7. (B1, B2, B3) (B1, B2, B3) 7. (B1, B2, B3)  (T1, T2, T3) 8. goto 2 (T1, T2, T3) 8. goto 2
Throughout the computation, the following relationships hold: | | mT1 + bT2 = T3 | mA1 + bA2 = A3 | mB1 + bB2 = B3 |
To see that this algorithm correctly returns gcd(m, b), note that if we equate A and B in the Euclidean algorithm with A3 and B3 in the extended Euclidean algorithm, then the treatment of the two variables is identical. At each iteration of the Euclidean algorithm, A is set equal to the previous value of B and B is set equal to the previous value of A mod B. Similarly, at each step of the extended Euclidean algorithm, A3 is set equal to the previous value of B3, and B3 is set equal to the previous value of A3 minus the integer quotient of A3 multiplied by B3. This latter value is simply the remainder of A3 divided by B3, which is A3 mod B3.
[Page 112] Note also that if gcd(m, b) = 1, then on the final step we would have B3 = 0 and A3 = 1. Therefore, on the preceding step, B3 = 1. But if B3 = 1, then we can say the following: mB1 + bB2 = B3 mB1 + bB2 = 1 bB2 = 1 mB1 bB2  1 (mod m) 1 (mod m) And B2 is the multiplicative inverse of b, modulo m. | Table 4.4 is an example of the execution of the algorithm. It shows that gcd(1759, 550) = 1 and that the multiplicative inverse of 550 is 355; that is, 550 x 335  1 (mod 1759). 1 (mod 1759). Table 4.4. Finding the Multiplicative Inverse of 550 in GF(1759)Q | A1 | A2 | A3 | B1 | B2 | B3 |
|---|
| 1 | 0 | 1759 | 0 | 1 | 550 | 3 | 0 | 1 | 550 | 1 | 3 | 109 | 5 | 1 | 3 | 109 | 5 | 16 | 5 | 21 | 5 | 16 | 5 | 106 | 339 | 4 | 1 | 106 | 339 | 4 | 111 | 355 | 1 |
|
For a more detailed proof of this algorithm, see [KNUT97]. Summary In this section, we have shown how to construct a finite field of order p, where p is prime. Specifically, we defined GF(p) with the following properties: GF(p) consists of p elements. The binary operations + and x are defined over the set. The operations of addition, subtraction, multiplication, and division can be performed without leaving the set. Each element of the set other than 0 has a multiplicative inverse.
We have shown that the elements of GF(p) are the integers {0, 1,..., p} and that the arithmetic operations are addition and multiplication mod p. |
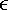 Z
Z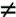 0, there exists a
0, there exists a  1 (mod
1 (mod 

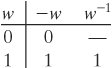

 (1, 0,
(1, 0,  (A1 QB1, A2 QB2, A3 QB3)
(A1 QB1, A2 QB2, A3 QB3)  1 (mod m)
1 (mod m)