Using Vectors

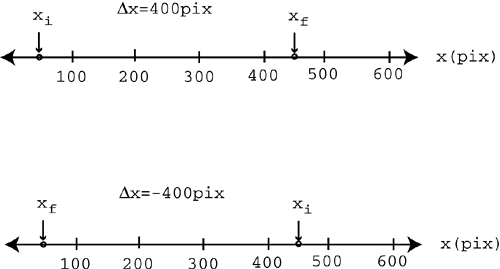
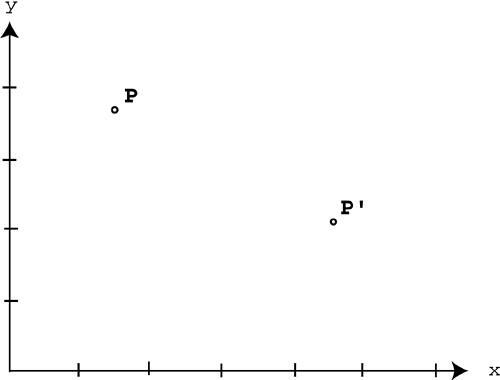
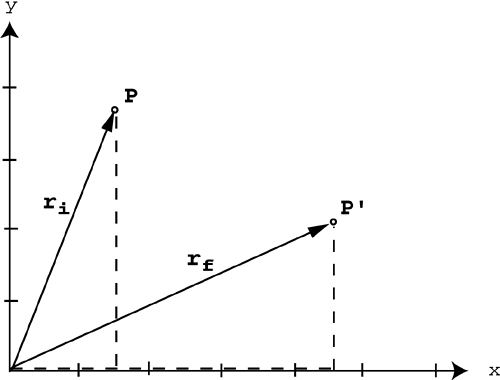
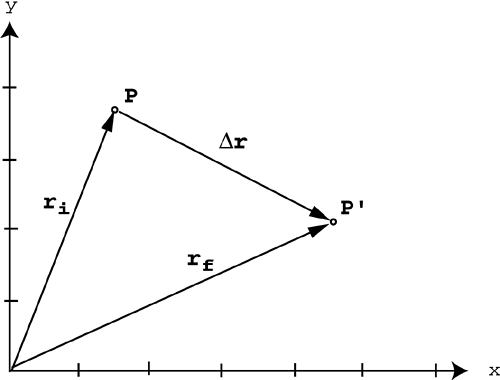
The biggest difference between one-dimensional and two- or three-dimensional motion involves the direction. Remember that displacement, velocity, and acceleration are all vector quantities and that in one dimension we satisfied the direction requirement with either a positive or negative sign.

However, to completely describe motion in two or three dimensions, we must incorporate vectors. This means that all the vector operations discussed in Chapter 4 can be applied to displacement, velocity, and acceleration. Believe it or not, this section has no new information. It simply combines the concepts of motion discussed in Chapter 8, "Motion in One Dimension," with the vector operations discussed in Chapter 4.

Let's start by revisiting the idea of displacement. In one dimension, there are only two possible directionspositive or negative. Displacement in 1D is the same as motion up and down a number line. For example, in Figure 10.1 the first object moves from the 50-pixel mark to the 450-pixel mark, so the total displacement is positive 400 pixels. Below that, the second object moves from the 450-pixel mark to the 50-pixel mark, so its displacement is 400 pixels.

Figure 10.1. Displacement in 1D.

In two dimensions, we're no longer restricted to two directions. Now there are 360 worth of directions. This means that positive or negative is no longer descriptive enough. We need to incorporate vectors. In 2D displacement is still final position minus initial position, but now we need to use vectors to describe those positions . So rather than subtract two numbers on a number line, now we must subtract two vectors. Remember that vectors must be in component form before you can subtract them. Look at the two positions in Figure 10.2P and P'.

Figure 10.2. Initial and final positions in 2D.

You can use 2D vectors anchored at the origin to describe those positions. Because you need to subtract them, you must express the two vectors in component form (distance in the x direction and distance in the y direction). Figure 10.3 shows the two vectors in component form.

Figure 10.3. Positions in 2D as vectors.

NOTE

When you venture into 2D, you can no longer use x for position, because each position has both x and y components . To avoid confusion, we will use r to represent position and D r for displacement in 2D.

Now we can talk about displacement. Remember that displacement is simply final position minus initial position, so all you have to do is subtract the two position vectors ( r _f r _i ). The displacement vector ( D r ) is shown in Figure 10.4.

Figure 10.4. Displacement in 2D.

2D Displacement

D r = r _f r _I

for position vectors r _i (initial) and r _f (final).

Example 10.1: Finding Displacement in 2D

Suppose an object in your game moves from point P(50,400) to point P'(550,100). What is its displacement?

Solution

1. Express the initial and final positions as vectors: P = [50 400] and P' = [550 100].

2. Displacement is change in position, so

   P' P = [550 100] [50 400] = [500 300]

3. The overall displacement is 500 pixels to the right and 300 pixels down, which written as a vector is [500 300].

When you use vectors for position and displacement, it's very simple to extend the process to 3D: You simply add a z component to all the vectors. Then all you have to do is subtract two 3D vectors.

Example 10.2: Finding Displacement in 3D

Suppose an object in your game moves from point P(150,0,250) to point P'(400,250,300). What is its displacement?

Solution

1. Express the initial and final positions as vectors: P = [150 0 250] and P' = [400 250 300].

2. Displacement is change in position, so

   P' P = [400 250 300] [150 0 250] = [250 250 550]

3. The overall displacement is 250 pixels to the right, 250 pixels up, and 550 pixels back, which written as a vector is [250 250 550].

If we take a look at Chapter 4 where we defined our 3Dvector class, solving this problem in our code would be extremely easy. We'd simply need to define our initial and final positions as vectors, then use the subtraction operator (which we defined) to return our solution:

 #include "3Dvector.h" int main() {     // Define our 2 vectors     3Dvector initial(150, 0, 250);     3Dvector final(400, 250, -300);     // Calculate our solution     3Dvector displacement = final  initial;     return 0; } 

Let's look back at the definition of velocity in one dimension. Velocity is the rate of change of position. In two dimensions velocity is still displacement divided by time. The only difference is that now displacement is a 2D or 3D vector instead of a positive or negative number. This means that to calculate average velocity, you need to divide the vector displacement by the scalar time.

If the vector is in polar coordinates, simply divide the magnitude by time and keep the direction the same. If it's in Cartesian coordinates, divide each component by time. In either case, the definition is the same.

Average Velocity in 2D and 3D

for any displacement vector D r and time interval t .

Example 10.3: Calculating Average Velocity in 3D

Suppose a character in your game moves from point P(150,0,250) to point P'(400,250,300) in 5 seconds. What is its average velocity over the 5-second time interval?

Solution

1. In Example 10.2, you found the displacement between points P and P'. The displacement vector was [250 250 550].

2. The average velocity is displacement divided by time. Because you have displacement in Cartesian coordinates, all you have to do is divide each component by the 5 seconds:

   

   
   

Calculating average velocity is extremely important for nterpolation and keyframing animations. When creating and loading 3D animations in a game, we use keyframing to save memory by storing only the initial and final frames of the animations, then calculating all of the in-between positions in the code. Once again, using our 3Dvector class defined in Chapter 4, a function to calculate average velocity would look like this:

 3Dvector averageVelocity(const 3Dvector &Pi, const 3Dvector &Pf,                   float intervals) {     // Calculate the displacement between our start and finish     3Dvector temp(Pf.x  Pi.x, Pf.y  Pi.y, Pf.z  Pi.z);     // Divide our displacement by our number of intervals     temp = temp * (1 / intervals);     // Return our answer     return temp; } 

As you might have guessed, the definition of acceleration, or the first equation of motion, also holds for 2D and 3D. Again, the only difference is that all the mathematical operations are performed on vectors instead of just scalar numbers. In fact, all the equations of motion work in 2D and 3D. The ones that are used most often in programming are the first, third, and fourth equations.

Equations of Motion in 2D and 3D

v _f = v _i + at

D x = ( v _f + v _i ) t

D x = v _i t + at ²

for vectors a , v _f , v _i , and D x and scalar t .

NOTE

These three equations are called parametric equations because they are functions of time. You'll find that they are used the most in game programming.

Here are the previous three equations as they would appear in code:

 // purpose: calculate final velocity, given initial velocity, acceleration, //          and time // input:   vi- initial velocity //          a-  acceleration //          t-  time // output:  our final velocity float eqOne_vf(float vi, float, a, float t) {     return vi + a * t; } // purpose: calculate change in distance, given final velocity, initial //          velocity, and time // input:   vf- final velocity //          vi- initial velocity //          t-  time // output:  our change in distance float eqTwo_x(float vf, float vi, float t) {      return .5f * (vf  vi) / t; } // purpose: calculate change in distance, given initial velocity, //           acceleration, and time // input:   vi- initial velocity //          t-  time //          a-  acceleration // output:  our change in distance float eqThree_x(float vi, float t, float a) {      return vi * t + .5f * a * t * t; } 

Any of these equations can be changed to solve for one of the other variables present in the equationfor instance, the third equation can be algebraically altered to solve for acceleration, and would appear as follows :

 // purpose: calculate acceleration, given initial velocity, //           change in distance, and time // input:   vi- initial velocity //          t-  change in distance //          a-  acceleration // output:  our acceleration float eqThree_a(float vi, float x, float a) {      return (x - vi * t) * 2 / (t * t); } 

These equations work the same way in two and three dimensions as they do in one dimension. Just remember that any time you add or subtract vector quantities, they must be in component form. Also, any time you must multiply a vector by time, simply multiply each component by the scalar quantity time.

Example 10.4: Using Equations of Motion in 2D

Suppose a vehicle in your game has a current velocity of 10m/s at 53 when it gets accelerated at a rate of 5m/s ² @ 30. How fast will it be going after 3 seconds?

Solution

1. Make a list of what you know and what you're looking for:

   Given	Find
   v i = 10m/s @ 53	v f = ?
   t = 3s
   a = 5m/s 2 @ 30

2. Because you've estimated the initial velocity and the acceleration in polar coordinates, you must convert them to Cartesian coordinates. Remember that the x-component is equal to the magnitude times the angle's cosine and that the y-component is equal to the magnitude times the angle's sine.

   Given	Find
   v i = 10m/s @ 53
   = [6 8]	v f = ?
   t = 3s
   a = 5m/s 2 @ 30
   = [4.3 2.5]

3. You need to choose an equation based on the list. In this case, the first equation ( v _f = v _i + at ) will work, because it is the only one that relates the four quantities in the list.

4. All that's left is to plug in and solve for v _f :

   v _f = v _i + at = [6 8] + [4.3 2.5]3 = [6 8] + [12.9 7.5] = [18.9 15.5]

   So v _f is the vector [18.9 15.5].

Example 10.5: Using Equations of Motion in 3D

Suppose you're coding a racing game like Need for Speed Under Ground and the car is at rest on the starting line. If the acceleration is given by the vector [3 0 2], how far will the care have gone 5 seconds after the start of the race?

Solution

1. Make a list of what you know and what you're looking for:

   Given	Find
   v i = [0 0 0]	D x = ?
   t = 5s
   a = [3 0 2]

2. Choose an equation based on the list. In this case, the fourth equation ( D x = v _i t + at ² ) will work, because it relates the three quantities you know with the one quantity you're looking for.

3. All that's left is to plug in and solve for D x :

   D x = v _i t + at ² = [0 0 0]5 + [3 0 2](5) ²

   =[0 0 0] + 12.5[3 0 2]

   =[37.5 0 25]

   So the displacement vector is [37.5 0 25].

As you can see, everything that was discussed in Chapter 8 also works in two and three dimensions. The only complication is the way in which vector quantities such as displacement, velocity, and acceleration are handled. The formulas still work; you just have to use vector operations instead of the scalar operations you're used to. The beauty of vector quantities is that they can always be broken into components, which simplifies the mathematical operations.

Self-Assessment

1.	Give a vector in both forms that can be used to describe the 2D position of (40,75).
2.	Find the displacement between the following two points on the screen: (250,300) and (75,100).
3.	Find the displacement between the two 3D points (20,30,40) and (50,0,50).
4.	Find the average velocity of an object that goes from the point (150,200) to (25,0) in 10 seconds.
5.	Find the average velocity of an object that goes from the point (50,400,50) to (250,100,100) in 10 seconds.
6.	Find the acceleration of an object that goes from 30m/s @ 30 to 25m/s @ 45 in 5 seconds.
7.	Find the displacement of the object described in question 6.
8.	Suppose an object in your game starts at rest, and its acceleration is given by the vector [4 1 2]. How far will it have gone after 5 seconds?
9.	How fast will the object described in question 8 be going at the end of the 5 seconds?