Cross Product
| < Day Day Up > |
| The preceding section looked at one way to "multiply" vectorsthe dot product. This section examines the cross product. The biggest difference between the two is that the dot product returns a scalar value and the cross product returns another vector. Let's look at the method for calculating the cross product. NOTE Some math texts refer to the cross product of two vectors as the vector product because that is what the cross product returns.
Example 4.15: Cross ProductFind the cross product of vectors A = [5 6 0] and B = [1 2 3]. SolutionThe cross product returns another vector, so you can calculate each component using the formula just described. A x B = [( a 2 b 3 a 3 b 2 ) ( a 3 b 1 a 1 b 3 ) ( a 1 b 2 a 2 b 1 )] = [(6(3) 0(2)) (0(1) 5(3)) (5(2) 6(1))] = [(18 0) (0 15) (10 + 6)] = [18 15 16] NOTE After you practice calculating a few cross products, you might notice the pattern for which it was named. Just be careful with all the plus and minus signs; it's very easy to make an error. The most notable characteristic of the cross product is that it returns another vector that is perpendicular to both the original vectors. For this reason, it only makes sense to apply the cross product to 3D vectors.
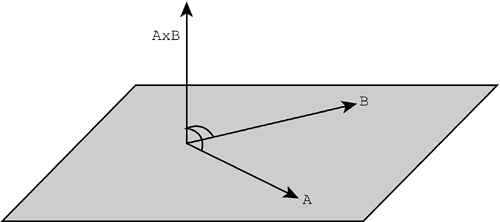
When you try to visualize the cross product, as shown in Figure 4.20, you might notice that it has two possible directions. Figure 4.20. A x B. The plane that contains vectors A and B has two perpendicular directions, "up" and "down." You can use the right-hand rule to determine which direction is given by the cross product. Place your right wrist at the point where A and B intersect, with your fingers pointing along A. As you curl your fingers toward B, your thumb points in the direction of A x B. Try reversing A and B; you should find that you get the opposite direction for B x A.
Because the cross product has the unique property of producing a third vector perpendicular to the original two, you can use the cross product to calculate the surface normal . Any two 3D vectors can define a surface. The surface normal is a vector that is perpendicular to the surface, and it has a length of 1. Now that we've covered the important vector operations, it's time to construct a fully functional 3D vector class. Something to be careful of when naming your class is to avoid calling it simply "vector," as there is already a vector class defined in the Microsoft STL libraries. This code can be typed directly into a header (*.h) file and compiled as-is. #ifndef _3DVECTOR_H_ #define _3DVECTOR_H_ class 3Dvector { private: float x, y, z; public: // purpose: Our constructor // input: ex- our vector's i component // why- our vector's j component // zee- our vector's k component // output: no explicit output 3Dvector(float ex = 0, float why = 0, float zee = 0) { x = ex; y = why; z = zee; } // purpose: Our destructor // input: none // output: none ~3Dvector() { } // purpose: calculate the magnitude of our invoking vector // input: no explicit input // output: the magnitude of our invoking object float getMagnitude() { return sqrtf(x * x + y * y + z * z); } // purpose: multiply our vector by a scalar value // input: num - the scalar value being multiplied // output: our newly created vector 3Dvector operator*(float num) const { return 3Dvector(x * num, y * num, z * num); } // purpose: multiply our vector by a scalar value // input: num - the scalar value being multiplied // vec - the vector we are multiplying to // output: our newly created vector friend 3Dvector operator*(float num, const 3Dvector &vec) { return 3Dvector(vec.x * num, vec.y * num, vec.z * num); } // purpose: Adding two vectors // input: vec - the vector being added to our invoking object // output: our newly created sum of the two vectors 3Dvector operator+(const 3Dvector &vec) const { return 3Dvector(x + vec.x, y + vec.y, z + vec.z); } // purpose: Subtracting two vectors // input: vec - the vector being subtracted from our invoking object // output: our newly created difference of the two vectors 3Dvector operator-(const 3Dvector &vec) const { return 3Dvector(x - vec.x, y - vec.y, z - vec.z); } // purpose: Normalize our invoking vector *this changes our vector* // input: no explicit input // output: none void normalize3Dvector(void) { float mag = sqrtf(x * x + y * y + z * z); x /= mag; y /= mag; z /= mag } // purpose: Dot Product two vectors // input: vec - the vector being dotted with our invoking object // output: the dot product of the two vectors float dot3Dvector(const 3Dvector &vec) const { return x * vec.x + y * vec.y + z * vec.z; } // purpose: Cross product two vectors // input: vec- the vector being crossed with our invoking object // output: our newly created resultant vector 3Dvector cross3Dvector(const 3Dvector &vec) const { return 3Dvector(y * vec.z z * vec.y, z * vec.x x * vec.z, x * vec.y y * vec.x); } }; #endif
Example 4.16: Surface NormalA surface is defined by two vectors, A = [5 2 0] and B = [1 2 3]. Find the surface normal so that it can be used to determine the resulting motion after a collision. Solution
Let's use the already-created 3Dvector class to solve this problem: #include <iostream> using namespace std; #include "3Dvector.h" int main() { // Let's define our two vectors 3Dvector A(5, -2, 0); 3Dvector B(1, 2, 3); // Calculate our cross product 3Dvector C = A.cross3Dvector(B); // Normalize our new vector C.normalize3Dvector(); // Print our answer to the screen cout << C.x << "i " << C.y << "j " << C.z << "k\n"; return 0; } Last, you can also use the cross product to calculate the angle between two vectors. When you're given a choice, the dot product is faster for finding the angle. However, if you already have the cross product calculated, it might be easier to use the following method.
Example 4.17: The Angle Between Two VectorsFind the angle between vectors A = [5 2 0] and B = [1 2 3]. Solution
Now let's add this function into our defined class for calculating the angle between two vectors: float angleBetween3Dvectors(const 3Dvector &vec) const { return (acos(dot3Dvector(vec) / (getMagnitude() * vec.getMagnitude())) * (180 / PI); } This section first defined the cross product. Remember that the cross product returns another 3D vector, and the dot product returns a scalar value. We also revisited the process of normalization when we calculated the surface normal. Also, the cross product can be used to calculate the angle between two vectors in almost the same way as the dot product. Now that we've discussed both types of "vector multiplication," you'll see them in action in C++ code in the next section. Self-Assessment
|
| < Day Day Up > |
EAN: 2147483647
Pages: 143
 B x A
B x A 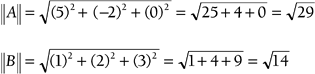
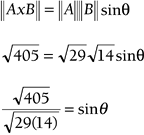
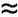 sin q
sin q