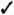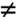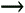Applications in Collision Detection

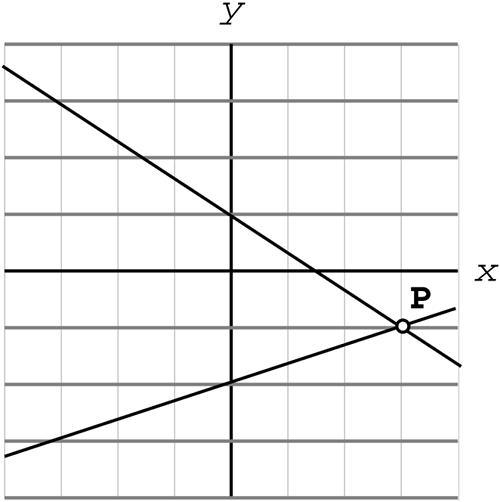
There will be times in game programming when you'll want to know if and where two lines intersect. The lines might represent the side of a building or the ground or the path of an object. You might need to program a conditional based on the intersection of two such lines. Now that you know how to find the equations of these lines, you can put the two equations together to form a system of linear equations . Then you can solve the system mathematically. This section first discusses the three types of solutions you might find, and then it describes methods of finding the numeric solution.

When solving a system of two linear equations, you're really searching for the intersection of two lines. The solution set is the set of all the points that satisfy both equations. Figures 1.17, 1.18, and 1.19 illustrate the three possible outcomes for a system of two linear equations. In Figure 1.17, the two lines

2 x + 3y = 3

x + 3 y = 6

Figure 1.17. Two lines intersecting at one point.

intersect at exactly one point. This point is labeled P, and on the graph it looks as if P has the coordinates (3,1). This is easy to verify; just plug these coordinates into each equation to check. The graph doesn't always show the point of intersection so clearly. The next section looks at how to calculate the point of intersection numerically .

2(3) + 3(1) = 3

6 3 = 3

(3) + 3(1) = 6

3 3 = 6

Notice that the graphs of these two lines have different slopes.

In Figure 1.18, the lines

3 x + 6 y = 6

x + 2 y = 2

Figure 1.18. Two lines that coincide.

coincide, or overlap. This time the solution set is not just one point; it's the infinite set of all the points on either line. Notice that the graphs of these two equations have the same slope and the same y-intercept.

Finally, in Figure 1.19, the two lines

x + 2 y = 2

x + 2 y = 2

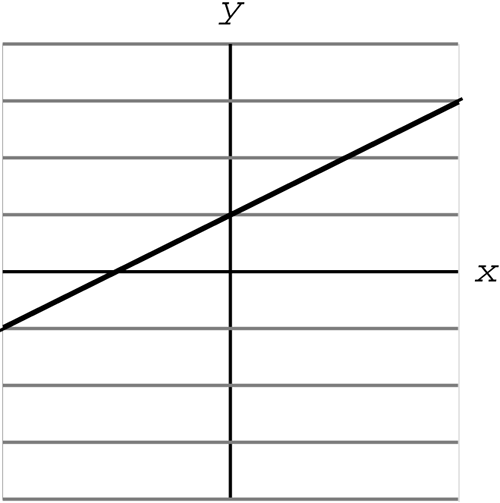
Figure 1.19. Two lines that never intersect.

are parallel. The solution set is the empty set, because the two equations have no points in common. They will never intersect. Notice that the graphs of these two equations have the same slope but different y-intercepts.

As you can see, the number of solutions for a system of linear equations is related to the slope and the y-intercept of the equations. Let's summarize the three possibilities.

Theorem

A system of two linear equations in the same plane has

• Exactly one solution if the two graphs have different slopes.

• An infinite set of solutions if both graphs have the same slope and y-intercept.

• No solution if the graphs have the same slope but different y-intercepts.

This is a very systematic procedure that can quickly and easily be implemented in code. Here is the algorithm, or step-by-step process, in pseudocode:

Find the slope of both lines, m ₁ and m ₂ .

1. If m ₁ m ₂ , output one solution.

2. If m ₁ = m ₂ , find the y-intercept of both lines, b ₁ and b ₂ .

   If b ₁ b ₂ , output zero solutions.

   If b ₁ = b ₂ , output infinite solutions.

Example 1.11: A System of Linear Equations

Graph the following system of linear equations (two lines), and state the size of the solution set (specify how many points of intersection exist).

x + y = 2

x + 2 y = 2

Solution

Both lines are graphed in Figure 1.20. It looks as though they intersect at one point close to the point (2,0). The graph isn't always so clear, so verify it numerically using the algorithm:

1. Find both slopes, m ₁ and m ₂ . Both lines are in standard form, so you can use the A/B shortcut.

   m ₁ = 1/1 = 1

   m ₂ = (1)/2 =

2. The slopes are not the same ( m ₁ m ₂ ), so there must be one point of intersection.

Figure 1.20. A graph of two lines in Example 1.11.

Example 1.12: Line-Line Collision Detection

A ball on the screen is moving along the straight path described by the line x + 2 y = 2. A wall has been placed along the line 3 x 6 y = 6. Will the ball ever hit the wall?

Solution

You could graph these two lines like you did in Example 1.11, but the graphs can sometimes be misleading, so go straight to the algorithm.

1. You might find that it's easier to pick off the slope and the y-intercept by putting both lines in slope-intercept form:

   x + 2 y = 2 y = x 1

   3 x 6 y = 6 y = x + 1

2. Find both slopes: m ₁ = and m ₂ = .

3. If m ₁ = m ₂ , find both y-intercepts: b ₁ = 1 and b ₂ = 1.

4. If b ₁ b ₂ , output zero solutions, because they are parallel and will never intersect. This means that the ball will never hit the wall.

This algorithm is very important to use when you're expecting two lines to intersect. What would happen if, in the preceding example, you were expecting the ball to hit the wall? That's rightyou'd get stuck in an infinite loop waiting for something that will never happen. This check can save you headaches in the long run, so verify in the code that the two lines will in fact intersect if that's a crucial part of the gameplay. It's a quick check, so why not use it?

After you've checked to see that two lines intersect at one point, you might want to know what that point of intersection is. You can find its coordinates using one of two methods: linear combination or substitution. You might have heard the expression "two equations with two unknowns." This refers to two linear equations with two variables you need to findin this case, x and y . Either of these two methods will work anytime you have two equations and two variables for which to solve.

Let's discuss linear combination first. Basically, you use the properties of equality to transform the system of equations into an equivalent system that is easier to work with. You do this by multiplying both sides of an equation by the same nonzero number. You want to multiply each equation by some number so that both equations have either the same x coefficient or the same y coefficient. (Remember that the coefficient is the number in front of the x or the y .) Suppose you have the following system of two linear equations:

3 x + 2 y = 10

4 x + 3 y = 6

Try to transform the system so that both equations have the same y coefficient. To do that, you must first multiply both sides of the top equation by 3. That gives you 9 x + 6 y = 30, which is still equal to 3 x + 2 y = 10. Then you multiply both sides of the bottom equation by 2 to get 8 x + 6 y = 12. This gives you an equivalent system (the same two lines), only this time the y coefficients are equal:

9 x + 6 y = 30

8 x + 6 y = 12

The next step is to combine the two equations into one. You do this by subtracting one from the other. Subtract the bottom one from the top one:

9 x + 6 y = 30

(8 x + 6 y = 12)

x + 0 y = 18

x = 18

The equation x = 18 is called the linear combination of the two original equations. Now you know that the x-coordinate of the solution is 18. All you have to do now is plug 18 back into one of the original equations to find the y-coordinate. If you plug 18 in for x in the top equation, you get

3(18) + 2 y = 10

so y = 22

Therefore, the solution to this system of equations is (18,22). What does this mean? Remember that the solution is the point where the two lines intersect. The following summarizes the steps of the linear combination method:

1. Choose which variable you'd like to eliminate ( x or y ).

2. Multiply both sides of each equation by some nonzero number so that the coefficients of the variable you are trying to eliminate match. (Keep in mind that it's much easier to work with small numbers .)

3. Subtract one equation from the other to find the system's linear combination.

4. Solve for the solution's first variable.

5. Substitute that back into one of the original equations to solve for the other variable.

It might help to step through an example using this new method.

Example 1.13: Finding the Point of Intersection Using the Linear Combination Method

A car in your game is traveling along a straight-line path defined by 3 x + 5 y = 8, and a wall is placed along another line defined by x + 3 y = 4. If the car continues on the same path, will it hit the wall? If so, at what point will it hit?

Solution

1. Check to see if the car will hit the wall. The slope of the first line is 3/5, and the slope of the second line is 1/3, so they will intersect.

2. Now you can use linear combination to find the exact point of intersection for these two lines:

   3 x + 5 y = 8

   x + 3 y = 4

3. Choose the variable you'd like to eliminate. Try to get rid of the x variable.

4. You must multiply by nonzero numbers so that the x coefficients are equal. In this case all we have to do is multiply the bottom equation by 3 on both sides. That will give us an equivalent system of:

   3 x + 5 y = 8

   3 x + 9 y = 12

5. If you subtract the bottom equation from the top one, you get 0 x 4 y = 4.

   (You could have just as easily subtracted the top from the bottom; that would have worked too.)

6. The equation found in step 5 can be solved for y : 4 y = 4 can be reduced to y = 1.

7. Substitute 1 for y in one of the original equations to solve for x . It might be easier to use the bottom original equation.

8. Substituting for y , you get x + 3(1) = 4, or x = 1. So the solution must be the point (1, 1).

Now let's turn our attention to the second method of solving a system of two linear equations, which is substitution . This method requires a lot of simple algebra. You still have to find the solution one coordinate at a time. First you must choose one of the original equations and solve it in terms of one variable, which means that one variable is on one side of the equals sign while everything else is on the other side. Suppose one of the equations in your system is

x + 2 y = 5

To solve this equation in terms of x , you must subtract 2 y from both sides, which gives you

x = 2 y + 5

Then you substitute that equation for x in the system's second equation. So if the second equation is

3 x 2 y = 1

substituting gives you

3(2 y + 5) 2 y = 1

This is where all the algebra comes into play. At this point, you want to solve for y . If you perform the algebra properly, you will find that

3(2 y + 5) 2 y = 1

6 y + 15 2 y = 1

8 y + 15 = 1

8 y = 16

y = 2

The final step is the same as it would be with the linear combination method. You must plug 2 in for y in one of the original equations so that you can solve for x . If you plug it into the first equation, you get

x + 2(2) = 5

so x = 1

This means that the solution is the point (1, 2).

Just as we did for linear combination, let's review the steps for the substitution method:

1. Choose one of the original equations, and solve it in terms of one variable. (Get one variable on the left of the equals sign and everything else on the right.)

2. Substitute this equation into the other original equation. (At this point one of the variables should be eliminated.)

3. Solve for the remaining variable.

4. Substitute the value found in step 3 into one of the original equations to solve for the other variable.

Now let's step through another example.

Example 1.14: Finding the Point of Intersection Using the Substitution Method

Solve the following system using the substitution method:

3 x + y = 8

5 x 2 y = 9

Solution

1. Examine the two original equations. It will be easier to solve for y in the first equation, because it has a coefficient of 1. You can do this quickly by adding 3 x to each side. That gives you

   y = 3 x + 8

2. Substitute the equation from step 1 for y in the bottom original equation. The result is

   5 x 2(3 x + 8) = 9

   (As you can see, the y has been eliminated.)

3. Solve the equation found in step 2 for x :

   5 x 2(3 x + 8) = 9

   5 x 6 x 16 = 9

   x = 25

   x = 25

4. Substitute 25 for x in one of the original equations so that you can solve for y . If you plug it into the top equation, you get

   3(25) + y = 8

   so y = 67

This means that the solution is the point (25, 67).

Both of the methods discussed in this section can be used to solve any system of two linear equations that has exactly one solution. However, it might be easier to use substitution when one of the variables has a coefficient of 1. Otherwise, it might be easier to use the linear combination method. Knowing which method to use in a particular situation can save you a lot of time. That is why it's a good idea to be comfortable with both methods.

So we are now confronted with the question of how to define lines and check for collision between them in code. Consider if we define a line by its slope and any point along that line. In that instance, the equation for a line would look as follows :

y y1 = m(x x1)

where m is the slope of the line and (x1,y1) is any point along the line. Rewriting this in terms of y, and looking at two different lines, we get:

y = m1(x x1) + y1

y = m2(x x2) + y2

By setting the equations equal to each other and solving for x, we get:

x = (m1x1 m2x2 + y2 y1) / (m1 m2)

So, let's write a function which, when given two lines, will return their point of intersection. This function assumes that we have already established that these lines are not parallel:

 // purpose: find the point of intersection between two lines // input: L1Point- a 2D point along our first line //         L1Slope- the slope of our first line //         L2Point- a 2D point along our second line //         L2Slope- the slope of our second line // output: our array of float holding our point float *lineIntersect(float *L1Point, float L1Slope,                  float *L2Point, float L2Slope) {     // A temp array for holding our answer     float temp[2] = {0, 0};     // Solve for our x value of the solution     temp[0] = (L1Slope * L1Point[0]  L2Slope * L2Point[0] +              L2Point[1]  L1Point[1]) / (L1Slope  L2Slope);     // Use our new-found value to solve for our y value     temp[1] = L1Slope(temp[0]  L1Point[0]) + L1Point[1];     return temp; } 

Self-Assessment

Give the slope and y-intercept for each equation and the number of solutions for the system:

1.	x + y = 7
2.	x 3 y = 6
3.	x + 4 y = 8 x 3 y = 2 x + 3 y = 6 x /4 + y = 2
4.	x y = 5
5.	x + 3 y = 1
6.	3 x 5 y = 8 5 x + y = 0 2 x + 6 y = 5 3 x + 5 y = 8

Solve the following systems of linear equations using the linear combination method:

7.	6 x 5 y = 7
8.	1/2 x + 2 y = 3 x 7 y = 1 4 x 5 y = 24

Solve the following systems of linear equations using the substitution method:

9.	3 x 2 y = 6
10.	4 x + 3 y = 8 x + 5 y = 15 2 x + y = 6