5.6 Channel Capacity Calculation

The channel capacity for the indoor radio frequency environment can be calculated based on the received signal strength and the corresponding noise level. The received signal strength depends on the transmit signal power level and the indoor radio frequency channel loss. According to the FCC rule, 1 W of transmit power is allowed at a spectrum of 1 MHz. This translates to a power spectrum density level of 30 dBm/Hz. On the other hand, the FCC rule clearly states that the transmit power spectrum density is limited at 32 dBm/Hz in every 3-kHz bandwidth. According to Figures 5.11 and 5.12, the worst case channel losses are 70 and 78 dB at less than 30 ft for frequency bands of 2.4 and 5.7 GHz, respectively. The channel capacity can be calculated according to

Equation 5.58

The answer is expressed in terms of bits per hertz. Assuming a noise power spectrum density of 168 dBm/Hz. The channel capacity for the 2.4-GHz frequency band is shown by

Equation 5.59

corresponding to the signal power spectrum density of 32 70 = 102 dBm/Hz. For the same noise power spectrum density level, the channel capacity for the 5.7-GHz frequency band is shown by

Equation 5.60

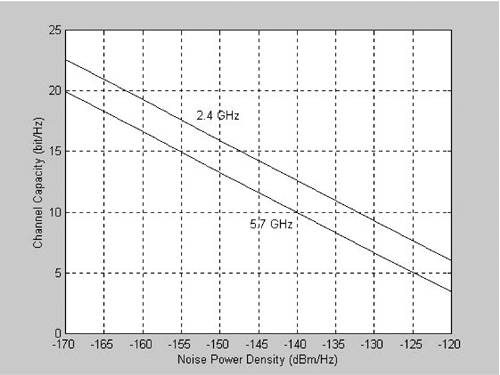
corresponding to the signal power spectrum density of 32 78 = 110 dBm/Hz. These calculations are based on a radio frequency interference-free environment where the noise floor is determined by the environment thermal noise. However, this indoor radio frequency channel is within an IMS band and the channel might be contaminated by radio frequency interference noise from other IMS band transmission systems. Figure 5.20 shows channel capacity figures corresponding to different noise power spectrum density levels for 2.4- and 5.7-GHz frequency bands, respectively. For a signaling bandwidth of 1 MHz, a channel capacity of 12 bits/Hz, which can be maintained with a noise power spectrum density level of 150 dBm/Hz, can be designed for a transmission system with a throughput of 10 Mbps. Figure 5.20 indicates that some research and study activities can be conducted for the development of high throughput, 10 Mbps and above, indoor radio frequency transmission systems.

Figure 5.20. Channel Capacity versus Noise Power Density