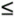4.5 Insightful Computing
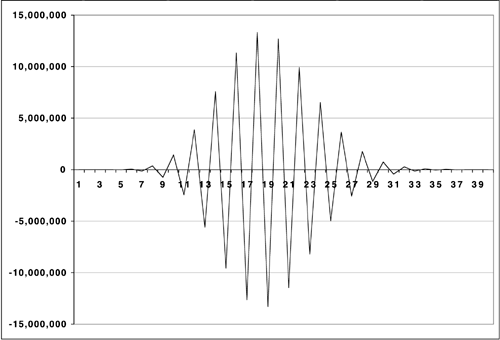
4.5 Insightful Computing At this point, you may be asking yourself, Why don't we just do everything with double-precision arithmetic and not worry about roundoff, magnitude, and cancellation errors? Double-precision numbers have larger exponent range (good for preventing underflow and overflow errors) and greater precision (good for minimizing roundoff errors). But they take up twice as much memory (bad for arrays), and their arithmetic is slower (bad for repeated computations ). Double-precision arithmetic will not hide the sins of bad design. Using double-precision arithmetic with carelessly designed computations will only delay the onset of floating-point errors. We need to study the nature of the problem to gain some insight, and then we may have to try several methods before we find one that works. To illustrate , the next few programs will compute the value of e x using its Taylor series at x = -19.5: Program 4 §C9 shows a first attempt and some of its output. See Listing 4-9. Listing 4-9 Computation of e - 19.5 using the Taylor series. package numbercruncher.program4_9; import numbercruncher.mathutils.AlignRight; /** * PROGRAM 4-9: e to x * * Compute e^x using the Taylor series with x = -19.5 * The final value should be approximately 3.4e-9 */ public class EtoX { private static final double x = -19.5; public static void main(String args[]) { AlignRight ar = new AlignRight(); int k = 0; double numerator = 1; double denominator = 1; double sum = 1; // running sum double prevSum = 0; // previous value of running sum ar.print("k", 2); ar.print("Numerator", 24); ar.println(); ar.print("Denominator", 26); ar.print("Fraction", 24); ar.print("Running sum", 23); ar.underline(); // Loop to compute and sum the terms of the Taylor series. do { numerator *= x; // x^k denominator *= ++k; // k! double fraction = numerator/denominator; prevSum = sum; sum += fraction; ar.print(k, 2); ar.print(numerator, 24); ar.println(); ar.print(denominator, 26); ar.print(fraction, 24); ar.print(sum, 23); ar.println(); } while (prevSum != sum); double correct = Math.exp(x); System.out.println("\ne^" + x + " = " + sum); System.out.println("% error = " + 100*Math.abs(sum - correct)/correct); } } Output: k Numerator Denominator Fraction Running sum ------------------------------------------------------------------------- 1 -19.5 1.0 -19.5 -18.5 2 380.25 2.0 190.125 171.625 3 -7414.875 6.0 -1235.8125 -1064.1875 4 144590.0625 24.0 6024.5859375 4960.3984375 ... 17 -8.522919630788428E21 3.55687428096E14 -2.3961824224183973E7 -1.2635486167179534E7 18 1.6619693280037435E23 6.402373705728E15 2.595864290953264E7 1.3323156742353106E7 19 -3.2408401896073E24 1.21645100408832E17 -2.6641765091362443E7 -1.3318608349009337E7 20 6.319638369734235E25 2.43290200817664E18 2.5975720964078385E7 1.2657112615069048E7 ... 49 -1.6281557854172669E63 6.082818640342675E62 -2.676646932425302 -0.754026189305919 50 3.1749037815636704E64 3.0414093201713376E64 1.0438923036458678 0.2898661143399488 51 -6.191062374049157E65 1.5511187532873822E66 -0.39913529257047886 -0.10926917823053006 52 1.2072571629395856E67 8.065817517094388E67 0.14967573471392956 0.0404065564833995 ... 90 1.2679876471392079E116 1.4857159644817607E138 8.534522596864606E-23 9.498996099055442E-9 91 -2.4725759119214553E117 1.3520015276784023E140 -1.828826270756701E-23 9.498996099055424E-9 92 4.821523028246838E118 1.24384140546413E142 3.876316552147356E-24 9.498996099055428E-9 93 -9.401969905081333E119 1.1567725070816409E144 -8.127760512567037E-25 9.498996099055428E-9 e^-19.5 = 9.498996099055428E-9 % error = 179.52464619068274 We immediately notice several things. The series converges very slowly, requiring 93 iterations before the fraction no longer affects the running sum. Because e - 19.5 The graph in Figure 4-4 plots the first 40 values of the running sum. Figure 4-4. The oscillating values of the running sum in Program 4 §C9. Thus, the value to which the running sum finally converges was determined by the "coarse tuning" that occurred earlier when its values first began to converge. The "fine tuning" at the end could not compensate for the earlier inaccuracies. The inaccuracies were due to roundoff errors ( especially with the very large numerator and denominator values), magnitude errors (many values of the running sum were several orders of magnitude greater than the final value of the sum), and cancellation errors (because of the alternating signs of the fractions). In fact, the roundoff errors in the large running sum values greatly exceed the final sum value. Also, if the series converges too slowly, the denominator will eventually overflow. Although it did not happen here with x = -19.5, larger absolute values of x will cause the numerator to overflow. Fixing the cancellation problem is easy. Since we can use the Taylor series with x and then take the inverse of the final sum if x is negative. Program 4-10 performs this computation. See Listing 4-10. Listing 4-10 Computation of e - 19.5 by inverting the result of the Taylor series at x = +19.5. package numbercruncher.program4_10; import numbercruncher.mathutils.AlignRight; /** * PROGRAM 4-10: e to x Inverse * * Compute e^x at x = -19.5 by using the Taylor series * with x = 19.5 and then taking the inverse of the result. * The final value should be approximately 3.4e-9 */ public class EtoXInverse { private static final double x = -19.5; public static void main(String args[]) { AlignRight ar = new AlignRight(); int k = 0; double numerator = 1; double denominator = 1; double sum = 1; // running sum double prevSum = 0; // previous value of running sum double xInverse = -x; ar.print("k", 2); ar.print("Numerator", 24); ar.println(); ar.print("Denominator", 26); ar.print("Fraction", 24); ar.print("Running sum", 23); ar.underline(); // Loop to compute and sum the terms of the Taylor series. do { numerator *= xInverse; // xInverse^k denominator *= ++k; // k! double fraction = numerator/denominator; prevSum = sum; sum += fraction; ar.print(k, 2); ar.print(numerator, 24); ar.println(); ar.print(denominator, 26); ar.print(fraction, 24); ar.print(sum, 23); ar.println(); } while (prevSum != sum); double result = 1/sum; double correct = Math.exp(x); System.out.println("\ne^" + x + " = " + result); System.out.println("% error = " + 100*Math.abs(result - correct)/correct); } } Output: k Numerator Denominator Fraction Running sum ------------------------------------------------------------------------- 1 19.5 1.0 19.5 20.5 2 380.25 2.0 190.125 210.625 3 7414.875 6.0 1235.8125 1446.4375 4 144590.0625 24.0 6024.5859375 7471.0234375 ... 63 1.871459856776355E81 1.98260831540444E87 9.4393826669419E-7 2.9426756604150844E8 64 3.649346720713892E82 1.2688693218588417E89 2.87606190633386E-7 2.9426756604150873E8 65 7.116226105392089E83 8.247650592082472E90 8.628185719001579E-8 2.942675660415088E8 66 1.3876640905514574E85 5.443449390774431E92 2.5492366897050122E-8 2.942675660415088E8 e^-19.5 = 3.3982678194950715E-9 % error = 1.217062127663519E-14 The final value is much improved. But the convergence is still quite slow, and we still run the risk of overflows in the numerator and in the denominator with larger absolute values of x. We need to increase the convergence rate, and we can accomplish that by reducing the sizes of the numerators. If the fractions are smaller, we'll reach the point sooner when the fractions are too small to affect the value of the running sum. Now for a bit of insight. We can split an exponent x into its whole w and fraction f components , where 0 If w is nonzero, we can reduce the size of the exponent by factoring out the whole part w: Since Program 4-11 computes e - 19.5 using this split exponent technique. See Listing 4-11. It uses the numbercruncher.mathutils.IntPower class from Chapter 2. Listing 4-11 Computation of e - 19.5 by splitting the exponent before using the Taylor series. package numbercruncher.program4_11; import numbercruncher.mathutils.IntPower; import numbercruncher.mathutils.AlignRight; /** * PROGRAM 4-11: e to x with Split Exponent * * Compute e^x by splitting the exponent x into its whole and * fraction components before using the Taylor series. */ public class EtoXSplit { private static final double x = -19.5; private static AlignRight ar = new AlignRight(); public static void main(String args[]) { double result; // Split off the whole part of x. double xAbs = Math.abs(x); int xWhole = (int) xAbs; // x is only a fraction. if (xWhole == 0) { result = taylor(xAbs); } // x has a whole part. else { // Split off the fraction part of x, // compute e^(1 + fraction/whole) ... double xFraction = xAbs - xWhole; double temp = taylor(1 + xFraction/xWhole); // ... and raise it to the whole power. result = IntPower.raise(temp, xWhole); } // Invert the result if x < 0. if (x < 0) result = 1/result; double correct = Math.exp(x); System.out.println("\ne " + x + " = " + result); System.out.println("% error = " + 100*Math.abs(result - correct)/correct); } /** * Compute e^x, x > 0 using the Taylor series. * @param x the exponent * @return the value to which the series converged */ private static double taylor(double x) { ar.print("k", 2); ar.print("Numerator", 20); ar.println(); ar.print("Denominator", 22); ar.print("Fraction", 24); ar.print("Running sum", 20); ar.underline(); int k = 0; double numerator = 1; double denominator = 1; double sum = 1; double prevSum = 0; // Loop until the terms have no effect on the sum. do { numerator *= x; // x^k denominator *= ++k; // k! double fraction = numerator/denominator; prevSum = sum; sum += fraction; ar.print(k, 2); ar.print(numerator, 20); ar.println(); ar.print(denominator, 22); ar.print(fraction, 24); ar.print(sum, 20); ar.println(); } while (prevSum != sum); return sum; } } Output: k Numerator Denominator Fraction Running sum ------------------------------------------------------------------ 1 1.0263157894736843 1.0 1.0263157894736843 2.026315789473684 2 1.0533240997229918 2.0 0.5266620498614959 2.55297783933518 3 1.0810431549788602 6.0 0.18017385916314335 2.733151698498323 4 1.1094916590572512 24.0 0.04622881912738547 2.7793805176257087 5 1.1386888079798105 120.0 0.009489073399831755 2.7888695910255406 6 1.1686543029266478 720.0 0.0016231309762870108 2.7904927220018276 7 1.1994083635299808 5040.0 2.3797784990674224E-4 2.7907306998517343 8 1.230971741517612 40320.0 3.053005311303601E-5 2.7907612299048474 9 1.263365734715444 362880.0 3.4814972848198965E-6 2.790764711402132 10 1.2966122014184822 3628800.0 3.5731156344204206E-7 2.7907650687136956 11 1.3307335751400213 3.99168E7 3.333768175655416E-8 2.7907651020513775 12 1.3657528797489693 4.790016E8 2.8512490976000275E-9 2.7907651049026265 13 1.4016937450055214 6.2270208E9 2.2509861296842326E-10 2.790765105127725 14 1.4385804225056669 8.71782912E10 1.6501590048437045E-11 2.7907651051442266 15 1.4764378020452897 1.307674368E12 1.1290561612088505E-12 2.7907651051453555 16 1.5152914284149028 2.0922789888E13 7.24230103406993E-14 2.790765105145428 17 1.5551675186363478 3.55687428096E14 4.372287001992683E-15 2.7907651051454323 18 1.596092979653094 6.402373705728E15 2.4929706590309163E-16 2.7907651051454327 19 1.6380954264860703 1.21645100408832E17 1.3466185000305503E-17 2.7907651051454327 e^-19.5 = 3.398267819495072E-9 % error = 2.434124255327038E-14 So our bit of insight has improved the convergence rate and produced a very accurate result. The error percentage is a bit higher here than in Program 4-10. But in general, splitting the exponent is the better technique. With a smaller numerator and faster convergence, the effects of accumulated roundoff errors and the chances for overflow are both reduced. |
| |
| Top |
EAN: 2147483647
Pages: 141

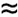 3.398267819495071 x 10 - 9 , the final computed value, although of the correct magnitude, is very wrong. The values of the running sum oscillate wildly before converging to its final (incorrect) value. Their magnitudes initially grow dramatically (
3.398267819495071 x 10 - 9 , the final computed value, although of the correct magnitude, is very wrong. The values of the running sum oscillate wildly before converging to its final (incorrect) value. Their magnitudes initially grow dramatically (