16.4 Newton s Algorithm in the Complex Plane

---

 

	Java Number Cruncher: The Java Programmer's Guide to Numerical Computing By Ronald  Mak
	Table of Contents
	Chapter  16.   Fractals

---

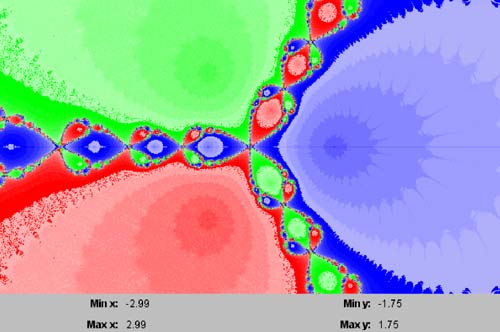
16.4 Newton's Algorithm in the Complex Plane

In Chapter 5, we examined Newton's algorithm, where the iteration formula was

We can also apply this formula in the complex plane. For example, consider the complex function f ( z ) = z ³ - 1, where z is a complex number. This function has three roots: 1, and . If we apply Newton's algorithm, the iteration formula is

and the three roots are each attracting fixed points.

Of course, for a point z in the complex plane, the number of iterations required to converge to one of the fixed points depends on the point's location. But what is intriguing is that the basins of attraction (the sets of points that converge their corresponding fixed points) do not cleanly separate the plane into three contiguous regions . Instead, their basins are intricately intertwined along their borders.

Program 16-3 plots this behavior by coloring each point in the complex plane red, green, or blue, depending on to which fixed point its orbit converges, and setting the color intensity based on the number of iterations needed to reach the fixed point. The result will be the fractal image of a Julia set. Listing 16-3 shows the program's class PlotThread.

Listing 16-3 Class PlotThread of Program 16 §C3, which plots the Julia set from applying Newton's algorithm to the complex function f(z) = z ³ - 1.

 private static final int     MAX_ITERS = 100; private static final Complex ONE       = new Complex(1, 0); private static final Complex THREE     = new Complex(3, 0); /**  * Graph thread class that applies Newton's Method to z^3 - 1  * starting at each point in the complex plane.  */ private class PlotThread extends Thread {     public void run()     {         // Loop over each graph panel pixel.         for (int r = 0; r < h; ++r) {             for (int c = 0; c < w; ++c) {                 if (stopFlag) return;                 // Convert the pixel coordinates to the                 // initial (x, y) in the complex plane.                 float x = xMin + c*delta;                 float y = yMax - r*delta;                 Complex z = new Complex(x, y);                 Complex zOld;                 // Loop until z converges.                 // Keep track of the number of iterations.                 int iters = 0;                 do {                     Complex zSquared = z.multiply(z);                     Complex zCubed   = zSquared.multiply(z);                     zOld = z;                     z = z.subtract(zCubed.subtract(ONE)                             .divide(THREE.multiply(zSquared)));                 } while ((++iters < MAX_ITERS)                             && (!z.equal(zOld)));                 // Set the color intensity based on                 // the number of iterations.                 int k = 20*(iters%10);                 // Set red, green, or blue according to                 // which root z converged to.                 if (z.real() > 0) {                     // 1                     plotPoint(c, r, new Color(k, k, 255));                 }                 else if (z.imaginary() > 0) {                     // -0.5+0.8660254i                     plotPoint(c, r, new Color(k, 255, k));                 }                 else {                     // -0.5-0.8660254i                     plotPoint(c, r, new Color(255, k, k));                 }             }             // Draw a row of the graph.             drawPlot();             yield();         }     } 

Screen 16-3 shows the program's initial output. Because it is a graph of a Julia set, we can repeatedly use the mouse to zoom into any rectangular region. Each zoomed-in region will resemble the larger region it was taken from.

Screen 16-3. The Julia set from applying Newton's algorithm to the complex function f(z) = z ³ - 1.

---

Top