12.4 Space Invaders

12.4 Space Invaders

The final example of a timed system is a simple video arcade game. The display is depicted in Figure 12.13. The spaceship can be moved around the screen using the cursor keys. Pressing the space bar on the keyboard launches a missile from the spaceship. Missiles move up the display and appear as white arrows on the display. Aliens, depicted as spheres, drop from the top of the screen and explode when hit by a missile. When an alien collides with the spaceship, an explosion occurs and the shield strength of the spaceship is reduced. The game terminates when the shield strength drops to zero. The objective, as is usual in this style of game, is to shoot as many aliens as possible.

Figure 12.13: Space Invaders applet display.

Video games involve many active entities, called sprites, which move around independently and concurrently. A sprite has a screen representation and a behavior. Sprites may interact when they collide. In Space Invaders, the sprites are the spaceship, aliens, missiles and explosions. Sprites are essentially concurrent activities, which we could consider implementing as threads. However, this would result in a game with poor performance due to the synchronization and context-switching overheads involved. A much better scheme is to implement sprites as timed objects. Each sprite has an opportunity to move once per clock cycle. This has the advantage that it is simple to synchronize screen updates with sprite activity. We simply repaint the screen once per clock cycle.

12.4.1 Space Invaders Model

Sprites move about in the two-dimensional space depicted in Figure 12.14. In an implementation, the coordinates refer to screen locations. In the model, we use a smaller space to permit analysis.

Figure 12.14: Game space.

The coordinate system is represented in the model by the following definitions. In the interests of simplicity, the width of the game space is assumed to be the same as its depth. The undef label is used to specify the coordinate of a sprite that has not been created and consequently does not have a defined position on the screen.

 const MAX = 4 range D   = 0..MAX set   Coord = {[D][D],undef} //(x,y)

Sprite

The entities that comprise the Space Invaders game have behavior in common with respect to the way that they move about in the game space. We model this common behavior as the SPRITE process listed below. The behavior of the spaceship, missiles and aliens is defined using this process.

 SPRITE =   (create[x:D][y:D] -> SPRITE[x][y]   |tick -> SPRITE   |pos.undef -> SPRITE   ), SPRITE[x:D][y:D] =   (pos[x][y] -> SPRITE[x][y]   |tick ->    (north -> if y>0   then SPRITE[x][y-1] else END    |south -> if y<MAX then SPRITE[x][y+1] else END    |west  -> if x>0   then SPRITE[x-1][y] else END    |east  -> if x<MAX then SPRITE[x+1][y] else END    | {rest,action[x][y]} -> SPRITE[x][y]    )   ), END = (end -> SPRITE).

Before a sprite is created, its location is undefined. A query using the action pos will return the undef value for its location. After the create action, pos returns a valid coordinate for the sprite’s current location. At each clock tick, a sprite can move in one of four directions, or it can remain in the same position (rest action). The sprite implementation described in the next section allows a sprite to move in one of eight directions; however, four directions are sufficient detail for modeling purposes. In addition to moving, a sprite can instigate an action during a clock cycle. When a sprite moves out of the game space, it indicates that it has terminated by performing the end action. In an implementation, a sprite would then be garbage collected. In the model, the sprite goes back to the state in which it can be created. As described in Chapter 9, we use cyclic behavior to model dynamic creation. The set of actions that the SPRITE process can engage in – excluding tick and the position query pos – is specified by:

 set Sprite =    {north,south,west,east,rest,action[D][D],create[D][D]}

Alien

An alien is a sprite that moves down the screen. Consequently, we can specify its behavior by constraining the movement of the SPRITE process. In the model, an alien starts at the top of the screen and moves vertically down; in the implementation, it can also move diagonally down.

 ALIEN_CONSTRAINT =   (create[D][0] -> MOVE), MOVE =   (south -> MOVE | end -> ALIEN_CONSTRAINT)   +Sprite. ||ALIEN = (SPRITE || ALIEN_CONSTRAINT).

The constraint permits an alien to be created at any x-position at the top of the screen and only permits it to move south and then end when it leaves the screen. The ALIEN composite process permits only these actions to occur since the constraint has the Sprite alphabet.

Missile

The behavior of the missile sprite is defined in exactly the same way. In this case, the missile is only permitted to move north, up the screen.

 MISSILE_CONSTRAINT =    (create[D][MAX] -> MOVE), MOVE =   (north -> MOVE | end -> MISSILE_CONSTRAINT)   + Sprite. ||MISSILE = (SPRITE || MISSILE_CONSTRAINT).

Spaceship

The spaceship has more complex behavior. It is constrained to moving horizontally at the bottom of the screen, either east or west, or staying in the same position, rest. It is created in the center of the screen and is constrained not to move off the screen. The spaceship can perform an action, which is used to create a missile, as explained later. In fact, the implementation permits the spaceship to move up and down the screen as well. However, horizontal movement is sufficient detail for us to gain an understanding of the operation of the system from the model.

 SPACESHIP_CONSTRAINT =    (create[MAX/2][MAX] -> MOVE[MAX/2]), MOVE[x:D] =    ( when (x>0) west -> MOVE[x-1]    | when (x<MAX) east -> MOVE[x+1]    | rest -> MOVE[x]    | action[x][MAX] -> MOVE[x]    ) + Sprite. ||SPACESHIP =(SPRITE || SPACESHIP_CONSTRAINT).

Collision Detection

Collision detection is modeled by the COLLIDE process which, after a tick, queries the positions of two sprites and signals a collision through the action explode if their positions coincide. Undefined positions are excluded. In the implementation, the detection of a collision results in the creation of an explosion sprite that displays a series of images to create the appropriate graphic appearance. In the model, we omit this detail.

 COLLIDE(A='a, B='b) =   (tick -> [A].pos[p1:Coord] -> [B].pos[p2:Coord]    -> if (p1==p2 && p1!='undef && p2!='undef) then          ([A][B].explode -> COLLIDE)       else          COLLIDE   ).

Space Invaders

The composite process SPACE_INVADERS models a game that, in addition to the spaceship, permits only a single alien and a single missile to appear on the screen. This simplification is required for a model of manageable size. However, we have defined sprites as having cyclic behavior that models recreation. Consequently, the alien can reappear in different start positions and the spaceship can launch another missile as soon as the previous one has left the screen. The model captures all possible behaviors of the combination of spaceship, alien and missile.

To model launching a missile, we have associated the spaceship’s action with the missile’s create by relabeling. Two collision detectors are included to detect spaceship – alien and alien – missile collisions.

 ||SPACE_INVADERS =    ( alien    :ALIEN    || spaceship:SPACESHIP    || missile :MISSILE    || COLLIDE('alien,'spaceship)    || COLLIDE('missile,'alien))    /{spaceship.action/missile.create,      tick/{alien,spaceship,missile}.tick}    >>{tick}.

Analysis

Safety analysis of SPACE_INVADERS does not detect a time-stop and progress analysis demonstrates that the TIME progress property is satisfied. Further, the progress properties:

 progress SHOOT_ALIEN={missile.alien.explode} progress ALIEN_SHIP ={alien.spaceship.explode}

are satisfied, showing that both alien – missile and alien – spaceship collisions can occur. To gain an understanding of the operation of the model, we can animate it to produce example execution traces. An alternative approach to producing sample traces is to use safety properties as follows. Suppose we wish to find a trace that results in a collision between an alien and a missile. We specify a safety property that the action missile.alien.explode should not occur and analyze the system with respect to this property:

 property ALIEN_HIT = STOP + {missile.alien.explode}. ||FIND_ALIEN_HIT = (SPACE_INVADERS || ALIEN_HIT).

The trace produced is:

 Trace to property violation in ALIEN_HIT:      alien.create.1.0      spaceship.create.2.4      tick      alien.south      spaceship.west      missile.pos.undef      alien.pos.1.1      spaceship.pos.1.4      tick      alien.south      spaceship.action.1.4 – missile launched      missile.pos.1.4      alien.pos.1.2      spaceship.pos.1.4      tick      alien.south      missile.north      missile.pos.1.3      alien.pos.1.3      missile.alien.explode

Exactly the same approach can be used to find a trace leading to a spaceship – alien collision.

The emphasis of the Space Invaders model is not so much on demonstrating that it satisfies specific safety and liveness properties but rather as a means of investigating interactions and architecture. After all, the program is far from a safety-critical application. However, in abstracting from implementation details concerned with the display and concentrating on interaction, the model provides a clear explanation of how the program should operate. In addition, it provides some indication of how the implementation should be structured. For example, it indicates that a CollisionDetector class is needed and confirms that a Sprite class can be used to implement the common behavior of missiles, aliens and the spaceship.

12.4.2 Space Invaders Implementation

The implementation of the Space Invaders program is large in comparison to the example programs presented previously. Consequently, we restrict ourselves to describing the structure of the program using class diagrams. The translation from timed processes to timed objects should be clear from examples presented in earlier sections of this chapter. The reader can find the Java code for each of the classes we mention on the website that accompanies this book.

Sprite and SpriteCanvas

The display for the Space Invaders program is handled by the two classes depicted in Figure 12.15. A Sprite is created with an initial position and an image. The SpriteCanvas maintains a list of sprites. Every clock tick, the SpriteCanvas calls the paint() method of each sprite on its list. The sprite then draws its image at its current position.

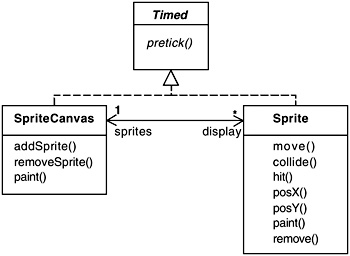
Figure 12.15: Sprite and SpriteCanvas classes.

The move() method has a direction parameter that specifies one of eight directions in which the sprite can move. It is called by a subclass each clock cycle to change the position of the sprite. The collide() method tests whether the sprite’s bounding rectangle intersects with the sprite passed as a parameter. The hit() method is called by the collision detector when a collision is detected. PosX() and PosY() return the current x and y coordinates of the sprite.

CollisionDetector

The collision detector maintains a list of the alien sprites and missile sprites and a reference to the spaceship sprite as shown in Figure 12.16. Every clock cycle, the detector determines whether each alien has collided with either a missile or the spaceship. If a collision is detected, the hit() methods of the sprites involved in the collision are invoked.

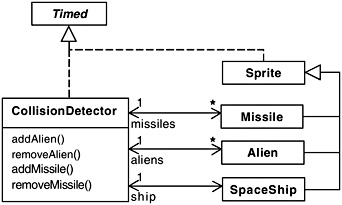
Figure 12.16: CollisionDetector class diagram.

The method listed below is the implementation provided for the hit() method in the Alien class.

 public void hit() {   new Explosion(this);   SpaceInvaders.score.alienHit();   SpaceInvaders.detector.removeAlien(this);   remove(); // remove from SpriteCanvas }

The method creates a new explosion sprite at the same location as the alien, records an alien hit on the scoreboard and removes the alien from the collision detector and the display. The CollisionDetector, Alien, Missile and Spaceship classes implement the essential behavior of the game. These classes correspond to the COLLIDE, ALIEN, MISSILE and SPACESHIP model processes.

SpaceInvaders

The SpaceInvaders applet class creates the spaceship, the alien generator, the missile launcher and the score board in addition to the display, time manager and collision detector as shown in Figure 12.17.

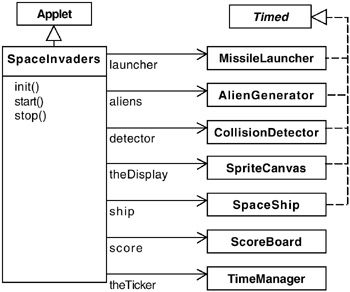
Figure 12.17: SpaceInvaders class diagram.

The AlienGenerator waits for a random number of clock cycles and then creates a new alien with a randomly chosen start position and a random downward direction. The MissileLauncher creates a new missile when the space bar is pressed. The x-coordinate of the new missile is the current position of the spaceship. The classes included in Figure 12.17 provide the infrastructure for scoring and the creation and display of sprites.

The collision detector and display run during the pre-tick clock phase; the remaining program actions, such as sprite movement, occur during the tick phase. This permits the display to render a consistent set of positions and for the effect of hits to be computed during tick processing. However, in reality, we could implement this sort of program using only a single-phase clock. This is because the clock ticks rapidly and, since the screen is updated every cycle, any inconsistencies which resulted from an action happening over two clock cycles rather than one would not be visible to a user.