Procedures
The 80×86 architecture enables implementation of procedures that are similar to those in a high-level language. Procedures use the hardware stack for several purposes. This chapter begins with a discussion of the 80×86 stack and then turns to important procedure concepts-how to call a procedure and return from one, parameter passing, local data, and recursion. The concluding section describes how procedures are implemented in one architecture that does not have a hardware stack.
The 80×86 Stack
Programs in this book have allocated stacks with the code
.STACK 4096
This .STACK directive tells the assembler to reserve 4096 bytes of uninitialized storage. The operating system initializes ESP to the address of the first byte above the 4096 bytes in the stack. A larger or smaller stack could be allocated, depending on the anticipated usage in the program.
The stack is most often used by pushing words or doublewords on it or by popping them off it. This pushing or popping is done automatically as part of the execution of call and return instructions (Section 6.2). It is also done manually with push and pop instructions. This section covers the mechanics of push and pop instructions, describing how they affect the contents of the stack.
Source code for a push instruction has the syntax
push source
The source operand can be a register 16, a register 32, a segment register, a word in memory, a doubleword in memory, an immediate byte, an immediate word, or an immediate doubleword. The only byte-size operand is immediate, and as you will see, multiple bytes are pushed on the stack for an immediate byte operand. Figure 6.1 lists the allowable operand types. The usual mnemonic for a push instruction is just push. However, if there is ambiguity about the size of the operand (as would be with a small immediate value), then you can use pushw or pushd mnemonics to specify word or doublewordsize operands, respectively.
|
Clock Cycles |
Number |
||||
|---|---|---|---|---|---|
|
Operand |
386 |
486 |
Pentium |
of Bytes |
Opcode |
|
register |
2 |
1 |
1 |
1 |
|
|
EAX or AX |
50 |
||||
|
ECX or CX |
51 |
||||
|
EDX or DX |
52 |
||||
|
EBX or BX |
53 |
||||
|
ESP or SP |
54 |
||||
|
EBP or BP |
55 |
||||
|
ESI or SI |
56 |
||||
|
EDI or DI |
57 |
||||
|
segment register |
2 |
3 |
1 |
||
|
CS |
1 |
0E |
|||
|
DS |
1 |
1E |
|||
|
ES |
1 |
06 |
|||
|
SS |
1 |
16 |
|||
|
FS |
2 |
0F A0 |
|||
|
GS |
2 |
0F A8 |
|||
|
memory word |
5 |
4 |
2 |
2+ |
FF |
|
memory doubleword |
5 |
4 |
2 |
2+ |
FF |
|
immediate byte |
2 |
1 |
1 |
2 |
6A |
|
immediate word |
2 |
1 |
1 |
3 |
68 |
|
immediate doubleword |
2 |
1 |
1 |
5 |
68 |
Figure 6.1: push instructions
When a push instruction is executed for a word-size operand, the stack pointer ESP is decremented by 2. Recall that initially ESP contains the address of the byte just above the allocated space. Subtracting 2 makes ESP point to the top word in the stack. The operand is then stored at the address in ESP; that is, at the high-memory end of the stack space. Execution is similar for a doubleword-size operand, except that ESP is decremented by 4 before the operand is stored. The immediate byte operand is interesting. Although a single byte is stored in the instruction, it is sign-extended to a doubleword that is actually stored on the stack. The byte-size operand saves three bytes of object code, but no stack space at execution time.
Example Example
We now show an example of execution of two push instructions. It assumes that ESP initially contains 00600200. The first push instruction decrements ESP to 006001FE and then stores the contents of AX at that address. Notice that the low and high-order byte are reversed in memory. The second push decrements ESP to 006001FA and stores FFFFFF10 (−24010) at that address.
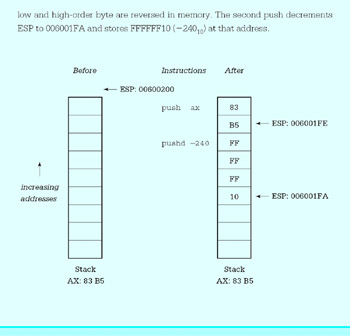
As additional operands are pushed onto the stack, ESP is decremented further and the new values are stored. No push instruction affects any flag bit.
Notice that a stack "grows downward," contrary to the image that you may have of a typical software stack. Also notice that the only value on the stack that is readily available is the last one pushed; it is at the address in ESP. Furthermore, ESP changes frequently as you push values and as procedure calls are made. In Section 6.3 you will learn a way to establish a fixed reference point in the middle of the stack using the EBP register, so that values near that point can be accessed without having to pop off all the intermediate values.
Pop instructions do the opposite job of push instructions. Each pop instruction has the format
pop destination
where destination can reference a word or doubleword in memory, any register 16, any register 32, or any segment register except CS. (The push instruction does not exclude CS.) The pop instruction gets a word-size value from the stack by copying the word at the address in ESP to the destination, then incrementing ESP by 2. Operation for a doubleword value is similar, except that ESP is incremented by 4. Figure 6.2 gives information about pop instructions for different destination operands.
|
Clock Cycles |
|||||
|---|---|---|---|---|---|
|
Operand |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
register |
4 |
1 |
1 |
1 |
|
|
EAX or AX |
58 |
||||
|
ECX or CX |
59 |
||||
|
EDX or DX |
5A |
||||
|
EBX or BX |
5B |
||||
|
ESP or SP |
5C |
||||
|
EBP or BP |
5D |
||||
|
ESI or SI |
5E |
||||
|
EDI or DI |
5F |
||||
|
segment register |
7 |
3 |
3 |
||
|
DS |
1 |
1F |
|||
|
ES |
1 |
07 |
|||
|
SS |
1 |
17 |
|||
|
FS |
2 |
0F A1 |
|||
|
GS |
2 |
0F A9 |
|||
|
memory word |
5 |
6 |
3 |
2+ |
8F |
|
memory doubleword |
5 |
6 |
3 |
2+ |
8F |
Figure 6.2: pop instructions
This example shows how pop instructions work. The doubleword at the address in ESP is copied to ECX before ESP is incremented by 4. The values popped from the stack are physically still there even though they logically have been removed. Note again that the bytes of a doubleword are stored backward in memory in the 80x86 architecture, but forward in the ECX register.

One use of push and pop instructions is to save the contents of a register temporarily on the stack. We have noted previously that registers are a scarce resource when programming. Suppose, for example, that you are using EDX to store some program variable but need to do a division that requires you to extend a dividend into EDXEAX prior to the operation. One way to avoid losing your value in EDX is to push it on the stack.
push edx ; save variable cdq ; extend dividend to doubleword idiv Divisor ; divide pop edx ; restore variable
This example assumes that you don't need the remainder the division operation puts in EDX. If you do need the remainder, it could be copied somewhere else before popping the value stored on the stack back to EDX.
As the above example shows, push and pop instructions are often used in pairs. When we examine how the stack is used to pass parameters to procedures, you will see a way to discard values from the stack without copying them to a destination location.
In addition to the ordinary push and pop instructions, special mnemonics push and pop flag registers. These mnemonics are pushf (pushfd for the extended flag register) and popf (popfd for the extended flag register). These are summarized in Fig. 6.3. They are often used in procedure code. Obviously popf and popfd instructions change flag values; these are the only push or pop instructions that change flags.
|
Clock Cycles |
|||||
|---|---|---|---|---|---|
|
Instruction |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
pushf |
4 |
4 |
3 |
1 |
9C |
|
pushfd |
|||||
|
popf |
5 |
9 |
4 |
1 |
9D |
|
popfd |
|||||
Figure 6.3: pushf and popf instructions
The 80x86 architecture has instructions that push or pop all general purpose registers with a single instruction. The pushad instruction pushes EAX, ECX, EDX, EBX, ESP, EBP, ESI and EDI, in this order. The value pushed for ESP is the address it contains before any of the registers are pushed. The popad instruction pops the same registers in the opposite order, except that the value for ESP is discarded. Popping the registers in the reverse order ensures that if these instructions are used in a pushad-popad pair, each register (except ESP) will get back its original value. Figure 6.4 shows the push all and pop all instructions, including the pusha and popa instructions that push and pop the 16-bit registers.
|
Clock Cycles |
|||||
|---|---|---|---|---|---|
|
Instruction |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
pusha |
18 |
11 |
5 |
1 |
60 |
|
pushad |
|||||
|
popa |
24 |
9 |
5 |
1 |
61 |
|
popad |
|||||
Figure 6.4: Push all and pop all instructions
Finally, a note of caution. Although the Intel architecture allows 16-bit or 32-bit quantities to be pushed on the stack, some operating systems (including Microsoft Windows NT) require parameters used in system calls to be on doubleword boundaries, that is, a parameter's address must be a multiple of 4. The stack starts on a doubleword boundary, but to maintain this alignment, only doublewords should be pushed on the stack prior to a system call. (See Chapter 12 for examples of system calls.)
Exercises 6.1
- For each instruction, give the opcode, the number of clock cycles for execution, and the number of bytes of object code. Assume that Double references a doubleword in memory. Assume a Pentium system for the number of clock cycles.
(a)
push ax
(b)
pushd 10
(c)
pusha
(d)
pop ebx
(e)
pop Double
(f)
popad
(g)
pushf
- For each part of this problem, assume the "before" values when the given instructions are executed. Give the requested "after" values. Trace execution of the instructions by drawing a picture of the stack
Before
Instructions
After
(a)
ESP: 06 00 10 00
CX: 01 A2push ecx
pushw 10ESP, ECX
(b)
ESP: 02 00 0B 7C
EBX: 12 34 56 78pushd 20
push ebxESP, EBX
(c)
ESP: 00 00 F8 3A
EAX: 12 34 56 78push eax
pushw 30
pop bx
pop ecxESP, EAX, BX, ECX
- Many microprocessors do not have an instruction equivalent to xchg. With such systems, a sequence of instructions like the following can be used to exchange the contents of two registers:
push eax push ebx pop eax pop ebx
Explain why this sequence works to exchange the contents of the EAX and EBX registers. Compare the number of bytes of code and clock cycles required to execute this sequence with those required for the instruction xchg eax,ebx.
- Another alternative to the xchg instruction is to use
push eax mov eax, ebx pop ebx
Explain why this sequence works to exchange the contents of the EAX and EBX registers. Compare the number of bytes of code and clock cycles required to execute this sequence with those required for the instruction xchg ax, bx.
Procedure Body, Call and Return
The word procedure is used in high-level languages to describe a subprogram that is almost a self-contained unit. The main program or another subprogram can call a procedure by including a statement that consists of the procedure name followed by a parenthesized list of arguments to be associated with the procedure's formal parameters.
Many high-level languages distinguish between a procedure that performs an action and a function that returns a value. A function is similar to a procedure except that it is called by using its name and argument list in an expression. It returns a value associated with its name; this value is then used in the expression. All subprograms in the C/C++ language are technically functions in this sense, but the language allows for functions that return no value.
In assembly language and in some high-level languages the term procedure is used to describe both types of subprograms, those that return values and those that do not. The term procedure will be used in both senses in this book.
Procedures are valuable in assembly language for the same reasons as in high-level languages. They help divide programs into manageable tasks and they isolate code that can be used multiple times within a single program or that can be saved and reused in several programs.
This section describes how to write 80x86 procedures, as well as how to assemble and link them using Microsoft software. Information is included on how to define a procedure, and how to transfer execution control to a procedure and back to the calling program. We show how the stack is used to save register contents, so that a procedure returns to the caller with almost all registers unchanged. Other important concepts to be considered with procedures are how to pass arguments to a procedure and how to implement local variables in a procedure body; these topics are covered in later sections.
The code for a procedure always follows a .CODE directive. The body of each procedure is bracketed by two directives, PROC and ENDP. Each of these directives has a label that gives the name of the procedure. With the Microsoft Macro Assembler, the PROC directive allows several attributes to be specified; we are only going to use one, NEAR32. This attribute says that the procedure will be located in the same code segment as the calling code and that 32-bit addresses are being used. These choices are normal for flat 32-bit memory model programming. Figure 6.5 shows relevant parts of a program that incorporates a procedure named Initialize. The job of the procedure is to initialize several variables; the calling program is sketched, but the code for the procedure itself is complete.
; procedure structure example ; Author: R. Detmer ; Date: revised 10/97 .386 .MODEL FLAT ExitProcess PROTO NEAR32 stdcall, dwExitCode:DWORD .STACK 4096 ; reserve 4096-byte stack .DATA ; reserve storage for data Count1 DWORD 11111111h Count2 DWORD 22222222h Total1 DWORD 33333333h Total2 DWORD 44444444h ; other data here .CODE ; program code Initialize PROC NEAR32 mov Count1,0 ; zero first count mov Count2,0 ; zero second count mov Total1,0 ; zero first total mov Total2,0 ; zero second total mov ebx,0 ; zero balance ret ; return Initialize ENDP _start: ; program entry point call Initialize ; initialize variables ; -- other program tasks here call Initialize ; reinitialize variables ; -- more program tasks here INVOKE ExitProcess, 0 ; exit with return code 0 PUBLIC _start ; make entry point public END ; end of source code
Figure 6.5: Procedure structure
In Fig. 6.5 the procedure Initialize is bracketed by PROC and ENDP. The distance attribute NEAR32 declares this to be a near procedure. Although this example shows the procedure body prior to the main code, it could also have been placed afterwards. Recall that execution of a program does not necessarily begin at the first statement of the code segment; the statement identified by the label _start marks the first instruction to be executed.
Most of the statements of procedure Initialize are ordinary mov instructions. These could have been used in the main program at the two places that the call statements are coded; however, using the procedure makes the main code both shorter and clearer. The procedure affects doublewords defined in the program's data segment and the EBX register; it has no local variables.
When the main program executes, the instruction
call Initialize
transfers control from the main code to the procedure. The main program calls the procedure twice; in general, a procedure may be called any number of times. The return instruction
ret
transfers control from the procedure back to the caller; there is almost always at least one ret instruction in a procedure and there can be more than one. If there is only one ret, it is ordinarily the last instruction in the procedure since subsequent instructions would be unreachable without "spaghetti code." Although a call instruction must identify its destination, the ret does not-control will transfer to the instruction following the most recent call. The 80x86 uses the stack to store the return address.
When the example program in Fig. 6.5 is assembled, linked, and executed, there is no visible output. However, it is informative to trace execution with a tool like WinDbg. Figure 6.6 show WinDbg's initial display. Note that ESP contains 0063FE3C. The memory window has been opened to start at address 0063FE30, 12 bytes down into the stack. The EIP register contains 0040103E, the address of the first instruction to be executed (the first call). Figure 6.7 shows the new state after this statement is executed. The EIP register now contains 00401010, the address of the first statement in procedure Initialize. The ESP register contains 0063FE38, so four bytes have been pushed onto the stack. Looking in memory at this address, you see 43 10 40 00-that is, 00401043, an address five bytes larger than the address of the first call. If you examine the listing file for the program, you see that the each call instruction takes five bytes of object code, so that 00401043 is the address of the instruction following the first call.
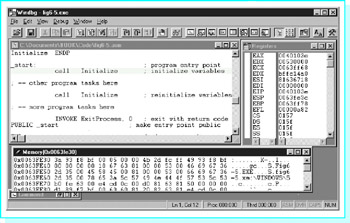
Figure 6.6: State prior to procedure call
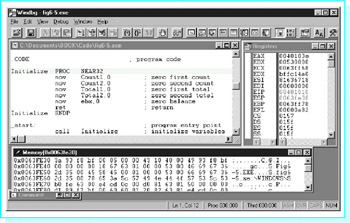
Figure 6.7: State after procedure call
In general, a call instruction pushes the address of the next instruction (the one immediately following the call) onto the stack and then transfers control to the procedure code. A near call instruction works by pushing the EIP to the stack and then changing EIP to contain the address of the first instruction of the procedure.
Return from a procedure is accomplished by reversing the above steps. A ret instruction pops EIP, so that the next instruction to be executed is the one at the address that was pushed on the stack.
Recall that 80x86 programming can be done using either a flat memory model or a segmented memory model. With a segmented memory model a procedure may be in a different segment from the calling code. In fact, with 16-bit segmented programming, segments were limited to 65,536 bytes, so procedures were often in separate segments. The 80x86 architecture uses a far call to transfer control to a procedure in a different memory segment: A far call pushes both EIP and CS onto the stack. A far return pops both off the stack. With 32-bit flat memory model programming, there is no need for anything other than near calls.
The syntax of the 80x86 call statement is
call destination
Figure 6.8 lists some of the available 80x86 call instructions, omitting 16-bit forms and forms used primarily for systems programming. The "+" notations on the timings for the 80386 processor indicate that there are additional clock cycles that depend on the next instruction. The program in Fig. 6.6 included a near procedure, designated by the PROC operand NEAR32. In general, the assembler determines whether destination references a near or far procedure from the PROC directive or from some other directive or operand. No call instruction modifies any flag.
|
Clock Cycles |
|||||
|---|---|---|---|---|---|
|
Operand |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
near relative |
7+ |
3 |
1 |
5 |
E8 |
|
near indirect |
FF |
||||
|
using register |
7+ |
5 |
2 |
2 |
|
|
using memory |
10+ |
5 |
2 |
2+ |
|
|
far direct |
17+ |
18 |
4 |
7 |
9A |
|
far indirect |
22+ |
17 |
5 |
6 |
FF |
Figure 6.8: call instructions
All of the procedures used in this book will be the first type, near relative. For a near relative procedure, the assembler calculates a 32-bit displacement to the destination, and the E8 opcode plus this displacement comprise the five bytes of the instruction. The transfer of control when a procedure is called is similar to the transfer of a relative jump, except that the old contents of EIP are pushed, of course.
Near indirect calls encode a register 32 or a reference to a doubleword in memory. When the call is executed, the contents of that register or doubleword are used as the address of the procedure. This makes it possible for a call instruction to go to different procedures different times.
All far calls must provide both new CS contents and new EIP contents. With far direct calls, both of these are coded in the instruction, adding six bytes to the opcode. With far indirect calls, these are located at a six-byte block in memory, and the address of that block is coded in the instruction.
The return instruction ret is used to transfer control from a procedure body back to the calling point. Its basic operation is simple; it pops the address previously stored on the stack and loads it into the instruction pointer EIP. Since the stack contains the address of the instruction following the call, execution will continue at that point. A near return just has to restore EIP. A far return instruction reverses the steps of a far call, restoring both EIP and CS; both of these values are popped from the stack.
There are two formats for the ret instruction. The more common form has no operand and is simply coded
ret
An alternative version has a single operand and is coded
ret count
The operand count is added to the contents of ESP after completion of the other steps of the return process (restoring EIP and, for a far procedure, CS). This can be useful if other values (parameters in particular) have been saved on the stack just for the procedure call, and can be logically discarded when the procedure is exited. (Parameters are discussed further in the next section.) Figure 6.9 lists the various formats of ret instructions.
|
Clock Cycles |
||||||
|---|---|---|---|---|---|---|
|
Type |
Operand |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
near |
none |
10+ |
5 |
2 |
1 |
C3 |
|
near |
immediate |
10+ |
5 |
3 |
3 |
C2 |
|
far |
none |
18+ |
13 |
4 |
1 |
CB |
|
far |
immediate |
18+ |
14 |
4 |
3 |
CA |
Figure 6.9: ret instructions
If a procedure's PROC directive has the operand NEAR32, then the assembler generates near calls to the procedure and near returns to exit from it. The Microsoft Macro Assembler also has retn (return near) and retf (return far) mnemonics to force near or far returns; we will not need these mnemonics.
To construct building blocks for large programs, it is often desirable to assemble a procedure or group of procedures separately from the code that calls them; that is, with procedures and calling programs in separate files. There are a few additional steps required to do this. First, you must assemble the procedures so that their names are visible outside the file containing them. Second, you must let the calling program know necessary information about the external procedures. Finally, you must link the additional .OBJ files to get an executable program.
The PUBLIC directive is used to make procedure names visible outside the file containing them. This is the same directive we have been using to make the symbol _start visible. In general, its syntax is
PUBLIC symbol1 [, symbol2]...
A file may contain more than one PUBLIC directive.
The EXTRN directive gives the calling program information about external symbols. It has many options, including
EXTRN symbol1:type [, symbol2:type]
A file may contain more than one EXTRN directive. Figure 6.10 outlines how this all fits together for two procedures, Procedure1 and Procedure2, which are assembled in a file separate from the main code. Note that .386 and .MODEL FLAT directives will also be required, and INCLUDE directives may be needed.
File containing procedure definitions PUBLIC Procedure1, Procedure2 .CODE Procedure1 PROC NEAR32 ... Procedure1 ENDP Procedure2 PROC NEAR32 ... Procedure2 ENDP END File containing procedure calls EXTRN Procedure1:NEAR32, Procedure2:NEAR32 ... .CODE ... call Procedure1 ... call Procedure2 ... END
Figure 6.10: Code for external procedures
You assemble each of the above files just as if it were the main program. Each assembly produces a .OBJ file. To link the files, simply list all .OBJ files in the link command-you already have been linking your programs with the separately assembled file IO.OBJ.
We conclude this section with a procedure that will calculate the integer square root of a positive integer Nbr; that is, the largest integer SqRt such that SqRt*SqRt ≤ Nbr. The procedure code is in Fig. 6.11. This is not a complete file ready for assembly; the procedure code could be assembled separately with the addition of the directives shown in Fig. 6.10, or it could be included in a file with a calling program.
; procedure to compute integer square root of number Nbr ; Nbr is passed to the procedure in EAX ; The square root SqRt is returned in EAX ; Other registers are unchanged. ; author: R. Detmer revised: 10/97 Root PROC NEAR32 push ebx ; save registers push ecx mov ebx, 0 ; SqRt := 0 WhileLE: mov ecx, ebx ; copy SqRt imul ecx, ebx ; SqRt*SqRt cmp ecx, eax ; SqRt*SqRt <= Nbr ? jnle EndWhileLE ; exit if not inc ebx ; add 1 to SqRt jmp WhileLE ; repeat EndWhileLE: dec ebx ; subtract 1 from SqRt mov eax, ebx ; return SqRt in AX pop ecx ; restore registers pop ebx ret ; return Root ENDP
Figure 6.11: Procedure to find integer square root
Procedure Root implements the following design.
Sqrt := 0; while Sqrt*Sqrt Nbr loop add 1 to SqRt; end while; subtract 1 from Sqrt;
This algorithm works by trying larger and larger integer candidates for SqRt; after it overshoots the correct value, it backs up one unit. This is not a very efficient technique, but it is easy to code.
The calling program must put the value for Nbr in the EAX register; the next section discusses a more common way of passing parameters to procedures. Procedure Root will return the value of SqRt in the EAX register; functions that return a single integer value frequently use the accumulator for this purpose.
In addition to the code that implements the design, the procedure contains two push instructions at the beginning, with corresponding pops immediately before the return. The purpose of these instructions is to preserve the contents of the EBX and ECX registers; that is, to return to the calling program with the same values in the registers as they had before call Root. This makes the procedure relatively independent of the calling program since someone using procedure Root does not have to worry about unexpected side-effects. This technique is extended in the next section.
Exercises 6.2
- Suppose that the NEAR32 procedure Exercise 1 is called by the instruction
call Exercise1
If this call statement is at address 00402000 and ESP contains 00406000 before the call, what return address will be on the stack when the first instruction of procedure Exercise 1 is executed? What will the value in ESP be?
- Why is the PUBLIC directive used when procedures are separately compiled? Why is the EXTRN directive used when procedures are separately compiled?
Programming Exercises 6.2
- Write a main program that will input an integer, call procedure Root (Fig. 6.11) to find the integer square root, and display the value of the square root. Include this program in the same file as procedure Root and assemble them together.
- Repeat Exercise 1, except assemble procedure Root and your main program in separate files.
- Write a procedure GetValue that prompts for and inputs an integer between 0 and a specified size MaxValue. A main program must send MaxValue to the procedure in the EAX register. Procedure GetValue will return the integer it inputs in EAX. Procedure GetValue will repeatedly prompt for input until the user enters a value in the specified range. Write procedure GetValue so that EAX is the only register changed upon return to the calling program; even the flags register must be unchanged.
Parameters and Local Variables
Using a high-level language, a procedure definition often includes parameters or formal parameters that are associated with arguments or actual parameters when the procedure is called. For the procedure’s in (pass-by-value) parameters, values of the arguments, which may be expressions, are copied to the parameters when the procedure is called, and these values are then referenced in the procedure using their local names, which are the identifiers used to define the parameters. In-out (pass-by-location or variable) parameters associate a parameter identifier with an argument that is a single variable and can be used to pass a value either to the procedure from the caller or from the procedure back to the caller. A common technique for passing parameters is discussed in this section. This technique can be used to pass word-size or doubleword-size values for in parameters, or addresses of data in the calling program for in-out parameters.
Although simple procedures can be written using only registers to pass parameters, most procedures use the stack to pass parameters. The stack is also frequently used to store local variables. As you will see, the techniques for using the stack for parameters and for local variables are closely related.
We start with a simple example to show how the stack is used to pass parameters. Suppose that the job of a NEAR32 procedure Add2 is to add two doubleword-size integers, returning the sum in EAX. If the calling program passes these parameters by pushing them on the stack, then its code might look like
push Value1 ; first argument value push ecx ; second argument value call Add2 ; call procedure to find sum add esp,8 ; remove parameters from stack
Before we look at how the parameter values are accessed from the stack, notice how they are removed from the stack following the call. There is no need to pop them off the stack to some destination; we simply add eight to the stack pointer to move ESP above the parameters. It is important to remove parameters from the stack since otherwise repeated procedure calls might exhaust the stack space. Even more serious, if procedure calls are nested and the inside call leaves parameters on the stack, then the outside return will not find the correct return address on the stack. An alternative to adding n to the stack pointer in the calling program is to use ret n in the procedure, the version of the return instruction that adds n to ESP after popping the return address. Both forms will be illustrated in this book.
Figure 6.12 shows how the procedure Add2 can retrieve the two parameter values from the stack. The procedure code uses the based addressing mode. In this mode, a memory address is calculated as the sum of the contents of a base register and a displacement built into the instruction. The Microsoft assembler accepts several alternative notations for a based address; this book will use [register+number], for example, [ebp+6]. Any general register (e.g., EAX, EBX, ECS, EDX, ESI, EDI, EBP, or ESP) can be used as the base register; EBP is the normal choice for accessing values in the stack.
Add2 PROC NEAR32 ; add two words passed on the stack ; return the sum in the EAX register push ebp ; save EBP mov ebp,esp ; establish stack frame mov eax,[ebp+8] ; copy second parameter ; value add eax,[ebp+12] ; add first parameter value pop ebp ; restore EBP ret ; return Add2 ENDP
Figure 6.12: Using parameter values passed on stack
This method of passing argument values works as follows. Upon entry to the procedure, the stack looks like the left illustration in Fig. 6.13. After the procedure’s instructions
push ebp ; save EBP mov ebp,esp ; establish stack frame
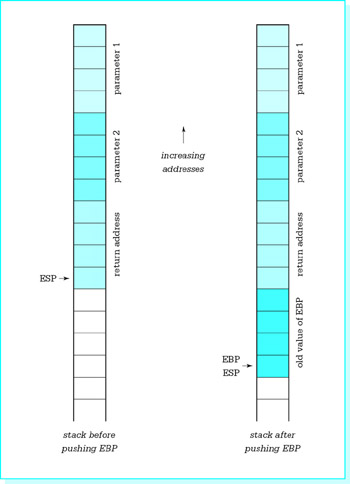
Figure 6.13: Locating parameters in the stack
are executed, the stack looks like the right illustration in Fig. 6.13.
Eight bytes are stored between the address stored in EBP (and also ESP) and the second parameter value. Therefore parameter 2 can be referenced by [bp+8]. The first parameter value is four bytes higher on the stack; its reference is [bp+12]. The code
mov eax,[bp+8] ; copy second parameter add eax,[bp+12] ; add first parameter
uses the values from memory locations in the stack to compute the desired sum.
You may wonder why EBP is used at all. Why not just use ESP as a base register? The principal reason is that ESP is likely to change, but the instruction mov ebp,esp loads EBP with a fixed reference point in the stack. This fixed reference point will not change as the stack used for other purposes—for example, to push additional registers or to call other procedures.
Some procedures need to allocate stack space for local variables, and most procedures need to save registers as illustrated in Fig. 6.11. Instructions to accomplish these tasks, along with the instructions
push ebp ; save EBP mov ebp,esp ; establish stack frame
make up the entry code for a procedure. However, the two instructions here are always the first entry code instructions. Because they are, you can count on the last parameter being exactly eight bytes above the reference point stored in EBP. The EBP register itself is always the first pushed and last popped so that upon return to the calling program it has the same value as prior to the call.
We now show how the stack can provide space for local variables. For this purpose, we revisit the algorithm for computing the greatest common divisor of two integers that appeared in Programming Exercises 5.3.
gcd := number1; remainder := number2; until (remainder = 0) loop dividend := gcd; gcd := remainder; remainder := dividend mod gcd; end until;
Figure 6.14 shows this design implemented as a NEAR32 procedure that computes the greatest common divisor of two doubleword-size integer values passed to the procedure on the stack, returning the GCD in EAX. Figure 6.14 includes more than the procedure itself. It shows a complete file, ready for separate assembly.
PUBLIC GCD ; Procedure to compute the greatest common divisor of two ; doubleword-size integer parameters passed on the stack. ; The GCD is returned in EAX. ; No other register is changed. Flags are unchanged. ; Author: R. Detmer Revised: 10/97 GCD PROC NEAR32 push ebp ; establish stack frame mov ebp,esp sub esp,4 ; space for one local doubleword push edx ; save EDX pushf ; save flags mov eax,[ebp+8] ; get Number1 mov [ebp--4],eax ; GCD := Number1 mov edx,[ebp+12] ; Remainder := Number1 until0: mov eax,[ebp--4] ; Dividend := GCD mov [ebp--4],edx ; GCD := Remainder mov edx,0 ; extend Dividend to doubleword div DWORD PTR [ebp--4] ; Remainder in EDX cmp edx, 0 ; remainder = 0? jnz until0 ; repeat if not mov eax,[ebp--4] ; copy GCD to EAX popf ; restore flags pop edx ; restore EDX mov esp,ebp ; restore ESP pop ebp ; restore EBP ret 8 ; return, discarding parameters GCD ENDP END
Figure 6.14: Greatest common divisor procedure
In this procedure, gcd is stored on the stack until it is time to return the value in EAX. The instruction
sub esp,4 ; space for one local doubleword
moves the stack pointer down four bytes, reserving one doubleword of space below where EBP was stored and above where other registers are stored. After EDX and the flags register are pushed, the stack has the contents shown in Fig. 6.15. Now the local variable gcd can be accessed as [ebp–4], since it is four bytes below the fixed reference point stored in EBP.
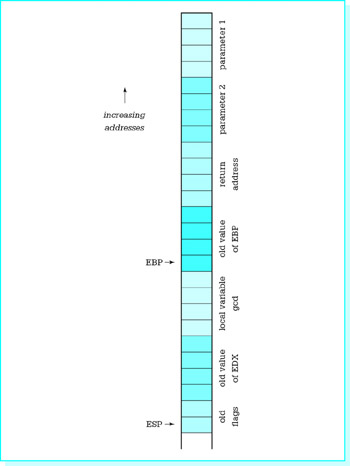
Figure 6.15: Stack usage with local variables
The rest of the procedure is a straightforward implementation of the design. In this example, a register could have been used to store gcd, but many procedures have too many local variables to store them all in registers. Within reason, you can reserve as many local variables on the stack as you wish, accessing each by [ebp-offset]. Notice that registers are saved after local variable space is reserved, so that the number of registers saved does not affect the offset down to a variable. Note also that most procedures will need to save more than two registers if register contents are to be unchanged upon return to the calling program.
Finally, consider the exit code for the procedure.
popf ; restore flags pop edx ; restore EDX mov esp,ebp ; restore ESP pop ebp ; restore EBP ret 8 ; return, discarding parameters
The first two pop instructions simply restore the flag register and EDX; these instructions are popped in the opposite order in which they were pushed. It may seem that the next instruction should be add sp,4 to undo the effects of the corresponding subtraction in the entry code. However, the instruction mov esp,ebp accomplishes the same objective more efficiently, working no matter how many bytes of local variable space were allocated, and without changing flags like an add instruction. Finally, we are using the ret instruction with operand 8, so that for this procedure the calling program must not remove parameters from the stack; this task is accomplished by the procedure.
Figure 6.16 summarizes typical entry code and exit code for a procedure. High-level language compilers generate similar code for subprograms. In fact, you can usually write an assembly language procedure that is called by a high-level language program with code like this. Check reference materials for the compiler before beginning since there are many variations of these techniques.
Entry code: push ebp ; establish stack frame mov ebp,esp sub esp,n ; n bytes of local variables space push ... ; save registers ... push ... pushf ; save flags Exit code: popf ; restore flags pop ... ; restore registers ... pop ... mov esp,ebp ; restore ESP if local variables used pop ebp ; restore EBP ret ; return
Figure 6.16: Typical procedure entry and exit code
How can a high-level language implement variable parameters? How can large parameters such as an array, a character string, or a record be efficiently passed to a procedure? Either of these can be implemented by passing the address of an argument rather than the value of the argument to the procedure. The procedure can then either use the value at the address or store a new value at the address. Figure 6.17 shows a procedure that might implement the Pascal procedure with header
PROCEDURE Minimum(A : IntegerArray; Count : INTEGER; VAR Min : INTEGER); (* Set Min to smallest value in A[1], A[2], ..., A[Count] *)
; Procedure to find the smallest word in array A[1..Count] ; Parameters: (1) address of array A ; (2) value of Count (word) ; (3) address of Min (destination for smallest) ; No register is changed. Flags are unchanged Minimum PROC NEAR32 push ebp ; establish stack frame mov ebp,esp pushad ; save all registers pushf ; save flags mov ebx,[ebp+14] ; get address of array A mov ecx, 0 ; ensure high order 0s in ECX mov cx,[ebp+12] ; get value of Count mov eax,7fffffffh ; smallest so far (MaxInt) jecxz endForCount ; exit when no elements to check forCount: cmp [ebx],eax ; element < smallest so far ? jnl endIfLess ; exit if not mov eax,[ebx] ; new smallest endIfLess: add ebx,4 ; address of next array element loop forCount ; iterate endForCount: mov ebx,[ebp+8] ; get address of Min mov [ebx],eax ; move smallest to Min popf ; restore flags popad ; restore registers pop ebp ; restore EBP ret ; return Minimum ENDP
Figure 6.17: Procedure using address parameters
In this implementation the addresses of arguments corresponding to A and Min are passed to procedure Minimum. The procedure uses register indirect addressing, first to examine each array element, and at the end to store the smallest value.
The instructions pushad and popad save and restore all general registers. These instructions are convenient, but they cannot be used if the procedure generates a value to be returned in a register. Note that since the Count parameter is word-size, the address of the first parameter is 14 bytes above the fixed base point—four bytes for EBP, four bytes for the return address, four bytes for the address of Min, and two bytes for the value of Count. (Draw the stack picture.)
Calling code for procedure Minimum could look like the following.
lea eax, Array ; Parameter 1: address of Array push eax push Count ; Parameter 2: value of Count lea eax, Min ; Parameter 3: address of Min push eax call Minimum ; call procedure add esp, 10 ; discard parameters
After this code is executed, the smallest value from Array will be in the word referenced by Min.
It is perfectly legal for a procedure to store local variables in the data segment. The .DATA directive can be included in a file used for separate assembly of procedures. In fact, a program may have multiple .DATA directives, although this is generally not necessary. You should normally keep variables as local as possible, stored on the stack or in part of the data segment that is visible only during assembly of the file containing the definitions. Even when a procedure and a calling program are assembled in a single file, you should avoid referencing the calling code’s variables directly in the procedure.
Because 80x86 instructions are often the output of a compiler, the 80x86 architecture includes additional instructions to facilitate implementation of procedures. The enter instruction has syntax
enter localBytes, nestingLevel
When nestingLevel is zero, this does precisely the job of the following familiar instructions:
push ebp mov ebp,esp sub esp, localBytes
that is, it establishes a stack frame and reserves the requested numbers of local bytes of storage. If nestingLevel > 0, the enter instruction also pushes the stack frame pointers from nestingLevel–1 levels back onto the stack above the new frame pointer. This gives this procedure easy access to the variables of procedures in which it is nested. If used, an enter instruction would normally be the first instruction in a procedure.
The leave instruction reverses the actions of the enter instruction. Specifically, it does the same thing as the instruction pair
mov esp,ebp ; restore ESP pop ebp ; restore EBP
and normally would be used immediately before a return instruction. We will not use the enter or leave instructions for procedures in this book.
You have observed that each program we write exits with the statement
INVOKE ExitProcess, 0 ; exit with return code 0
INVOKE is not an instruction—MASM references call it a directive. However, it acts more like a macro. In fact, if the directive .LISTALL precedes the above line of code, you see the expansion
push +000000000h call ExitProcess
This is clearly a call to procedure ExitProcess with a single doubleword parameter with value 0.
Exercises 6.3
- Suppose that a NEAR32 procedure begins with
push ebp ; save EBP mov ebp,esp ; new base pointer push ecx ; save registers push esi ...
Assume that this procedure has three parameters passed on the stack, (1) a doubleword, (2) a word, and (3) a second word. Draw a picture of the stack following execution of the above code. Include parameters, return address, and show the bytes to which EBP and ESP point. How can each parameter be referenced?
- Give entry code (Fig. 6.16) for a NEAR32 procedure that reserves eight bytes of storage on the stack for local variables. Assuming that this space is used for two doublewords, how can each local variable be referenced?
- Explain why you cannot use pushad and popad in a procedure that returns a value in EAX.
Programming Exercises 6.3
Write a NEAR32 procedure to perform each task specified below. For each procedure, use the stack to pass arguments to the procedure. Except for those problems that explicitly say to return a result in a register, register contents should be unchanged by the procedure; that is, registers, including the flags register, which are used in the procedure should be saved at the beginning of the procedure and restored before returning. Allocate stack space as needed for local variables. Use the ret instruction with no operand. For each problem, write a separately assembled test driver, a simple main program that will input appropriate values, call the procedure, and output results. The main program must remove arguments from the stack. Link and run each complete program.
- Write a procedure Min2 to find the minimum of two word-size integer parameters. Return the minimum in the AX register.
- Write a procedure Max3 to find the maximum of three doubleword-size integer parameters. Return the maximum in the EAX register.
- Write a procedure Avg to find the average of collection of doublewordsize integers in an array. Procedure Avg will have three parameters:
- the address of the array
- the number of integers in the array (passed as a doubleword)
- the address of a word at which to store the result.
- Write a procedure Search to search an array of doublewords for a specified doubleword value. Procedure Search will have three parameters:
- the value for which to search (a doubleword)
- the address of the array
- the number N of doublewords in the array (passed as a doubleword)
Return in EAX the position (1,2,…,N) at which the value is found, or return 0 if the value does not appear in the array.
Recursion
A recursive procedure or function is one that calls itself, either directly or indirectly. The best algorithms for manipulating many data structures are recursive. It is frequently very difficult to code certain algorithms in a programming language that does not support recursion.
It is almost as easy to code a recursive procedure in 80x86 assembly language as it is to code a nonrecursive procedure. If parameters are passed on the stack and local variables are stored on the stack, then each call of the procedure gets new storage allocated for its parameters and local variables. There is no danger of the arguments passed to one call of a procedure being confused with those for another call since each call has its own stack frame. If registers are properly saved and restored, then the same registers can be used by each call of the procedure.
This section gives one example of a recursive procedure in 80x86 assembly language. It solves the Towers of Hanoi puzzle, pictured in Fig. 6.18 with four disks. The object of the puzzle is to move all disks from source spindle A to destination spindle B, one at a time, never placing a larger disk on top of a smaller disk. Disks can be moved to spindle C, a spare spindle. For instance, if there are only two disks, the small disk can be moved from spindle A to C, the large one can be moved from A to B, and finally the small one can be moved from C to B.
Figure 6.18: Towers of Hanoi puzzle
In general, the Towers of Hanoi puzzle is solved by looking at two cases. If there is only one disk, then the single disk is simply moved from the source spindle to the destination. If the number of disks NbrDisks is greater than one, then the top (NbrDisks-1) disks are moved to the spare spindle, the largest one is moved to the destination, and finally the (NbrDisks-1) smaller disks are moved from the spare spindle to the destination. Each time (NbrDisks-1) disks are moved, exactly the same procedure is followed, except that different spindles have the roles of source, destination, and spare. Figure 6.19 expresses the algorithm in pseudocode.
procedure Move(NbrDisks, Source, Destination, Spare);
begin
if NbrDisks = 1
then
display "Move disk from ", Source, " to ", Destination
else
Move(NbrDisks -- 1, Source, Spare, Destination);
Move(1, Source, Destination, Spare);
Move(NbrDisks -- 1, Spare, Destination, Source);
end if;
end procedure Move;
begin {main program}
prompt for and input Number;
Move(Number, 'A', 'B', 'C');
end;
Figure 6.19: Pseudocode for Towers of Hanoi Solution
Figure 6.20 shows 80x86 code that implements the design. The stack is used to pass parameters to procedure Move, which is a NEAR32 procedure referencing the data segment for output only. A standard stack frame is established, and registers used by the procedure are saved and restored. The code is a fairly straightforward translation of the pseudocode design. The operator DWORD PTR is required in the statement
; program to print instructions for "Towers of Hanoi" puzzle
; author: R. Detmer revised: 10/97
.386
.MODEL FLAT
ExitProcess PROTO NEAR32 stdcall, dwExitCode:DWORD
include io.h ; header file for input/output
cr equ 0dh ; carriage return character
Lf equ 0ah ; line feed
.STACK 4096 ; reserve 4096-byte stack
.DATA ; reserve storage for data
prompt BYTE cr,Lf,'How many disks? ',0
number BYTE 16 DUP (?)
message BYTE cr,Lf,'Move disk from spindle '
source BYTE ?
BYTE ' to spindle '
dest BYTE ?
BYTE '.',0
.CODE
Move PROC NEAR32
; procedure Move(NbrDisks : integer; { number of disks to move }
; Source, Dest, Spare : character { spindles to use } )
; parameters are passed in words on the stack
push ebp ; save base pointer
mov ebp,esp ; copy stack pointer
push eax ; save registers
push ebx
cmp WORD PTR [ebp+14],1 ; NbrDisks = 1?
jne elseMore ; skip if more than 1
mov bx,[ebp+12] ; Source
mov source,bl ; copy character to output
mov bx,[ebp+10] ; destination
mov dest,bl ; copy character to output
output message ; print line
jmp endIfOne ; return
elseMore: mov ax,[ebp+14] ; get NbrDisks
dec ax ; NbrDisks - 1
push ax ; parameter 1: NbrDisks-1
pushw [ebp+12] ; parameter 2: source does not change
pushw [ebp+8] ; parameter 3: old spare is new destination
pushw [ebp+10] ; parameter 4: old destination is new spare
call Move ; Move(NbrDisks-1,Source,Spare,Destination)
add esp,8 ; remove parameters from stack
pushw 1 ; parameter 1: 1
pushw [ebp+12] ; parameter 2: source does not change
pushw [ebp+10] ; parameter 3: destination unchanged
pushw [ebp+8] ; parameter 4: spare unchanged
call Move ; Move(1,Source,Destination,Spare)
add esp,8 ; remove parameters from stack
push ax ; parameter 1: NbrDisks-1
pushw [ebp+8] ; parameter 2: source is original spare
pushw [ebp+10] ; parameter 3: original destination
pushw [ebp+12] ; parameter 4: original source is spare
call Move ; Move(NbrDisks-1,Spare,Destination,Source)
add esp,8 ; remove parameters from stack
endIfOne:
pop ebx ; restore registers
pop eax
pop ebp ; restore base pointer
ret ; return
Move ENDP
_start: output prompt ; ask for number of disks
input number,16 ; read ASCII characters
atoi number ; convert to integer
push ax ; argument 1: Number
mov al,'A' ; argument 2: ' A'
push ax
mov al,'B' ; argument 3: ' B'
push ax
mov al,'C' ; argument 4: ' C'
push ax
call Move ; Move(Number,Source,Dest,Spare)
add esp,8 ; remove parameters from stack
INVOKE ExitProcess, 0 ; exit with return code 0
PUBLIC _start ; make entry point public
END ; end of source code
Figure 6.20: Towers of Hanoi solution
cmp DWORD PTR [bp+14],1
so that the assembler knows whether to compare words or byte size operands. Similarly, the pushw mnemonic is used several places so that the assembler knows to push wordsize parameters. Notice that the recursive calls are implemented exactly the same way as the main program call, by pushing four parameters on the stack, calling procedure Move, then removing the parameters from the stack. However, in the main program the spindle parameters are constants, stored as the low order part of a word since single bytes cannot be pushed on the 80x86 stack.
Exercises 6.4
- What will go wrong in the Towers of Hanoi program if EAX is not saved at the beginning of procedure Move and restored at the end?
- Suppose that the Towers of Hanoi program is executed and 2 is entered for the number of disks. Trace the stack contents from the first push in the main program through the instruction add esp,8 in the main program.
Programming Exercises 6.4
- The factorial function is defined for a non-negative integer argument n by
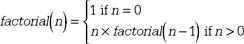
Write a recursive assembly language procedure named Factorial that implements this recursive definition. Use the stack to pass the single doubleword integer argument; return the value of the function in the EAX register. The calling program should remove the parameter from the stack. Test your function by calling it from a main program that inputs an integer, calls the Factorial function, and displays the value returned by the function. Why is it better to use doubleword-size than word-size integers for this function?
- The greatest common divisor (GCD) of two positive integers m and n can be calculated recursively by the function described below in pseudocode. function GCD(m, n : integer) : integer;
if n = 0 then return m; else Remainder := m mod n; return GCD(n, Remainder); end if;
Implement this recursive definition in assembly language. Use the stack to pass the two doubleword-size argument values. Return the value of the function in the EAX register. The procedure should remove the parameters from the stack. Test your function with a main program that inputs two integers, calls the greatest common divisor function GCD, and displays the value returned.
Other Architectures Procedures Without a Stack
Not all computer architectures provide a hardware stack. One can always implement a software stack by setting aside a block of memory, thinking of it as a stack, maintaining the stack top in a variable, and pushing or popping data by copying to or from the stack. However, this is much less convenient than having an architecture like the 80x86 that automatically adjusts the stack top for you as you push values, pop values, call procedures, and return from procedures.
Obviously the stack plays a large role in 80x86 procedure implementation. How can you reasonably implement procedures in an architecture that has no stack? This section gives a brief description of one system for doing this. It is based on the conventions commonly used in IBM mainframe computers whose architecture is derived from the System/360 (S/360) systems first introduced in the 1960s.
The S/360 architecture includes sixteen 32-bit general purpose registers (GPRs), numbered 0 to 15. Addresses are 24 bits long and an address can be stored in any register. The architecture includes addressing modes comparable to direct, register indirect, and indexed.
A procedure is usually called by loading its address into GPR 15 and then executing a branch and link instruction that jumps to the procedure code after copying the address of the next instruction into GPR 14. This makes return easy; simply jump to the address in GPR 14.
Parameter passing is more challenging. Normally GPR 1 is used to pass the address of a parameter address list. This is a list of 32-bit storage locations (32 bits is called a word in the S/360 architecture), the first word containing the address of the first parameter, the second word containing the address of the second parameter, etc. To retrieve a word-size parameter, one must first get its address from the parameter address list, then copy the word at that address.
Since the same general purpose registers are normally used for the same tasks each time a procedure is called, problems may occur if one procedure calls another. For instance, a second procedure call would put the second return address into GPR 14, wiping out the first return address. To avoid this problem, the main program and each procedure allocates a block of storage for a register save area and puts its address in GPR 13 prior to a procedure call. The procedure then saves general purpose registers 0-12, 14, and 15 in the register save area of the calling program and GPR 13 in its own register save area. This system is relatively complicated compared to using a stack, but it works well except for recursive procedure calls. Since there is only one register save area per procedure, recursive procedure calls are impossible without modifying the scheme.
Exercises 6.5
- If you translate the IBM S/360 parameter passing scheme into 80x86 assembly language, you get code that looks like the following in the calling program.
Double1 DWORD ? ... Value1 DWORD ? Value2 DWORD ? ... AddrList DWORD OFFSET Value1 ; address of parameter 1 DWORD OFFSET Value2 ; address of parameter 2 DWORD OFFSET Double1 ; address of parameter 3 ... lea ebx,AddrList ; get address of AddrList call Proc1
Note that the parameters do not need to be in consecutive storage locations, but their addresses are in consecutive words at AddrList. Give code to show how the values of the three parameters can be accessed from within procedure Proc1.
- Describe what happens if you attempt a recursive procedure call using the system described in this section.
Summary
This chapter has discussed techniques for implementing procedures in the 80x86 architecture. The stack serves several important purposes in procedure implementation. When a procedure is called, the address of the next instruction is stored on the stack before control transfers to the first instruction of the procedure. A return instruction retrieves this address from the stack in order to transfer control back to the correct point in the calling program. Argument values or their addresses can be pushed onto the stack to pass them to a procedure; when this is done, the base pointer EBP and based addressing provide a convenient mechanism for accessing the values in the procedure. The stack can be used to provide space for a procedure's local variables. The stack is also used to "preserve the environment"-for example, register contents can be pushed onto the stack when a procedure begins and popped off before returning to the calling program so that the calling program does not need to worry about what registers might be altered by the procedure.
Recursive algorithms arise naturally in many computing applications. Recursive procedures are no more difficult than nonrecursive procedures to implement in the 80x86 architecture.
Some computer architectures do not have a hardware stack. Nonrecursive procedures can be implemented using registers to store addresses, and memory to save registers when one procedure calls another.
Preface
- Representing Data in a Computer
- Parts of a Computer System
- Elements of Assembly Language
- Basic Instructions
- Branching and Looping
- Procedures
- String Operations
- Bit Manipulation
- The Assembly Process
- Floating-Point Arithmetic
- Decimal Arithmetic
- Input/Output
- Appendix A Hexadecimal/ASCII conversion
- Appendix B Useful MS-DOS Commands
- Appendix C MASM 6.11 Reserved Words
- Appendix D 80x86 Instructions (by Mnemonic)
- Appendix E 80x86 Instructions (by Opcode)
EAN: 2147483647
Pages: 113
