Basic Instructions
This chapter covers instructions used to copy data from one location to another and instructions used for integer arithmetic. It specifies what types of operands are allowed for the various instructions. The concepts of time and space efficiency are introduced. Finally, some methods are given for accomplishing equivalent operations even when the desired operand types are not allowed. After studying this chapter you will know how to copy data between memory and CPU registers, and between two registers. You will also know how to use 80×86 addition, subtraction, multiplication, and division instructions, and how execution of these instructions affects flags.
Copying Data
Most computer programs copy data from one location to another. With 80×86 machine language, this copying job is done by mov (move) instructions. Each mov instruction has the form
mov destination, source
and copies a byte, word, or doubleword value from the source operand location to the destination operand location. The value stored at the source location is not changed. The destination location must be the same size as the source. A mov instruction is similar to a simple assignment statement in a high-level language. For example, the Pascal or Ada assignment statement
Count := Number
might correspond directly to the assembly language instruction
mov Count, ecx ; Count := Number
assuming that the ECX register contains the value of Number and that Count references a doubleword in memory. The analogy between high-level language assignment statements and mov instructions cannot be carried too far. For example, the assignment statement
Count := 3*Number + 1
cannot be coded with a single mov instruction. Multiple instructions are required to evaluate the right-hand expression before the resulting value is copied to the destination location.
One limitation of the 80×86 architecture is that not all "logical" combinations of source and destination operands are allowed. In particular, you cannot have both source and destination in memory. The instruction
mov Count, Number ; illegal for two memory operands
is not allowed if both Count and Number reference memory locations.
All 80×86 mov instructions are coded with the same mnemonic. The assembler selects the correct opcode and other bytes of the machine code by looking at the operands as well as the mnemonic.
Figure 4.1 lists mov instructions that have an immediate source operand and a register destination operand. The number of clock cycles it takes to execute each instruction is given for 80386, 80486, and Pentium processors. Although little production programming is actually done in assembly language, some assembly language code is written in the interest of obtaining very efficient procedures. Time efficiency is often measured by the length of time it takes to execute a program, and this depends on the number of clock cycles it takes to execute its instructions. Space efficiency refers to the size of the code-a small executable file may be important if the program must be stored in ROM, for example. Figure 4.1 also shows the number of bytes for each instruction.
|
Destination |
Clock Cycles |
|||||
|---|---|---|---|---|---|---|
|
Operand |
Source Operand |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
register 8 |
immediate byte |
2 |
1 |
1 |
2 |
|
|
|
|||||
|
register 16 |
immediate word |
2 |
1 |
1 |
3 (plus prefix byte) |
|
|
|
|||||
|
register 32 |
immediate doubleword |
2 |
1 |
1 |
5 |
|
|
|
|||||
Figure 4.1: Immediate-to-register mov instructions
The length of time an instruction takes to execute is measured in clock cycles. To determine the actual time, you must know the clock speed of the processor. The Intel 8088 in the original IBM PC had a clock speed of 4.77 MHz; that is, 4,770,000 cycles per second. Many 80×86 personal computers now operate at speeds higher than 200 MHz; that is, 200,000,000 cycles per second. These rates translate into about 210 ns (ns = nanosecond, 10−9 seconds) per clock cycle for the original IBM PC or 5 ns per clock cycle for a 200 MHz machine. Microcomputers have gotten faster not only because of faster clock speeds, but because the same instructions often execute in fewer clock cycles for later members of the same processor family.
The number of bytes for each instruction is the same for the Intel 80386, 80486, and Pentium processors, which is because the object code is identical. It would also be the same for 8086, 8088, 80186, and 80286 processors except that no 32-bit registers were available, so the last third of Fig. 4.1 would not apply.
It may be surprising that the op codes for word and doubleword immediate-to-register mov instructions are identical. The 80×86 processor maintains a segment descriptor for each active segment. One bit of this descriptor determines whether operands are 16-bit or 32-bit length by default. With the assembler directives and link options used in this book, this bit is set to 1 to indicate 32-bit operands. Therefore, the B8 opcode means, for instance, to copy the immediate doubleword following the opcode to EAX, not an immediate word to AX. If you code the 16-bit instruction
mov ax, 0
then the assembler inserts the prefix byte 66 in front of the object code B8 0000, so that the code generated is actually 66 B8 0000. In general, the prefix byte 66 tells the assembler to switch from the default operand size (32-bit or 16-bit) to the alternative size (16-bit or 32-bit) for the single instruction that follows the prefix byte.
As was discussed in Chapter 2, instructions sometimes affect various flag bits in the EFLAGS register. In general, an instruction may have one of three effects:
- no flags are altered
- specific flags are given values depending on the results of the instruction
- some flags may be altered, but their settings cannot be predicted
All mov instructions fall in the first category: No mov instruction changes any flag.
Figure 4.2 lists the mov instructions that have an immediate source and a memory destination. Again, the 80486 and Pentium processors execute these instructions in a single clock cycle, while the 80386 takes two clock cycles. This is a relatively minor improvement compared to the original 8088, which took at least 14 clock cycles for each of these instructions.
|
Destination |
Clock Cycles |
|||||
|---|---|---|---|---|---|---|
|
Operand |
Source Operand |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
memory byte |
immediate byte |
2 |
1 |
1 |
C6 |
|
|
|
|
|||||
|
memory word |
immediate word |
2 |
1 |
1 |
C7 |
|
|
|
|||||
|
memory doubleword |
immediate doubleword |
2 |
1 |
1 |
C7 |
|
|
|
|||||
Figure 4.2: Immediate-to-memory mov instructions
The number of bytes taken by a memory operand depends on the type of operand. A direct operand must be encoded as a 32-bit address, four bytes. A register indirect operand is encoded as three bits in the second object code byte. We will later examine encodings of other types of memory operands. The 66 prefix byte is again required for 16-bit operands; it is not shown in the table since it is technically not part of the instruction.
The C6 and C7 opcodes listed in Fig. 4.2 for immediate-to-memory moves can also be used for immediate-to-register moves. However, these forms require an extra byte of object code, and an assembler normally chooses the shorter form given in Fig. 4.1.
Figure 4.3 lists most of the remaining 80×86 mov instructions. This table introduces some new terminology. Register 32 refers to one of the 32-bit registers EAX, EBX, ECX, EDX, EBP, ESI, EDI, or ESP. Similarly register 16 refers to one of the 16 bit registers AX, BX, CX, DX, SP, BP, SI or DI, and register 8 refers to an eight bit register, AL, AH, BL, BH, CL, CH, DL, or DH.
|
Clock Cycles 486 |
||||||
|---|---|---|---|---|---|---|
|
Destination Operand |
Source Operand |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
register 8 |
register 8 |
2 |
1 |
1 |
2 |
8A |
|
register 16 |
register 16 |
2 |
1 |
1 |
2 |
8B |
|
register 32 |
register 32 |
2 |
1 |
1 |
2 |
8B |
|
register 8 |
memory byte |
4 |
1 |
1 |
2-7 |
8A |
|
register 16 |
memory word |
4 |
1 |
1 |
2-7 |
8B |
|
register 32 |
memory doubleword |
4 |
1 |
1 |
2-7 |
8B |
|
AL |
direct memory byte |
4 |
1 |
1 |
5 |
A0 |
|
AX |
direct word |
4 |
1 |
1 |
5 |
A1 |
|
EAX |
direct doubleword |
4 |
1 |
1 |
5 |
A1 |
|
memory byte |
register 8 |
2 |
1 |
1 |
2-7 |
88 |
|
memory word |
register 16 |
2 |
1 |
1 |
2-7 |
89 |
|
memory doubleword |
register 32 |
2 |
1 |
1 |
2-7 |
89 |
|
direct memory byte |
AL |
2 |
1 |
1 |
5 |
A2 |
|
direct word |
AX |
2 |
1 |
1 |
5 |
A3 |
|
direct doubleword |
EAX |
2 |
1 |
1 |
5 |
A3 |
|
segment register |
register 16 |
2 |
3 |
1 |
2 |
8E |
|
register 16 |
segment register |
2 |
3 |
1 |
2 |
8C |
|
segment register |
memory word |
2 |
3+ |
2+ |
2-7 |
8E |
|
memory word |
segment register |
2 |
3 |
1 |
2-7 |
8C |
Figure 4.3: Additional mov instructions
Note that sometimes the same opcode is used for what appear to be distinct instructions, for example for a register 8 to register 8 move and for a memory byte to register 8 move. In these cases the second byte of the instruction determines not only the destination register, it also encodes the source register or indicates the mode of a memory source byte. The structure of this byte will be considered more in Chapter 9.
Two distinct instructions copy a memory operand to the accumulator. For example, either of opcodes A1 and 8B could be used to encode the instruction mov eax, Number. The difference is that the 8B instruction opcode can also be used to copy doublewords to other destination registers, while the A1 opcode is specific to the accumulator. An assembler normally uses the A1 version since it is one byte shorter.
It is important to realize that, particularly with older processors, instructions that access memory are slower than instructions that use data in registers. It should also be noted that instructions that access memory may require more than the number of clock cycles listed. One reason this can occur is memory that does not respond rapidly enough; in this case wait states, wasted clock cycles, are inserted until the memory responds. Even with fast memory, extra cycles can be required to access a word or doubleword that is not aligned in memory-that is, stored on an address that is a multiple of two or four, respectively. A programmer should plan to keep frequently-used data in registers when possible.
This book does not discuss mov instructions that copy data to and from special registers used primarily in systems programming.
When you first look at all the mov instructions summarized in Figs. 4.1-4.3, you may think that you can use them to copy any source value to any destination location. However, many seemingly logical combinations are not available. These include
- a move with both source and destination in memory
- immediate source to segment register destination
- any move to or from the flag register
- any move to the instruction pointer register
- a move from one segment register to another segment register
- any move where the operands are not the same size
- a move of several objects
You may need to do some of these operations. We describe below how to accomplish some of them.
Although there is no mov instruction to copy from a memory source to a memory destination, two moves using an intermediate register can accomplish the same thing. For doubleword length data referenced by Count and Number, the illegal instruction
mov Count, Number ; illegal for two memory operands
can be replaced by
mov eax, Number ; Count := Number mov Count, eax
each using the accumulator EAX and one direct memory operand. Some register other than EAX could be used, but each of these instructions using the accumulator requires five bytes, while each of the corresponding instructions using some other register takes six bytes-EAX is chosen in the interest of space efficiency.
To load an immediate value into a segment register, one can use an immediate to register 16 move, followed by a register 16 to segment register move. This sequence is needed to initialize the data segment register DS when coding with segmented memory models.
Although the flag register and the instruction pointer cannot be set by mov instructions, other instructions do change their values. The instruction pointer register is routinely updated as new instructions are fetched and it is automatically changed by jump, call, and return instructions. Individual flags are set by a variety of instructions, and it is possible and occasionally desirable to set all bits in the flag register to specified values; some techniques will be covered later.
To change the size of data from a word to a byte, it is legal, for example, to transfer a word to a register 16, and then move out just the high-order or low-order byte to a destination. Going the other way, one can piece together two bytes in the high and low bytes of a 16-bit register and then copy the resulting word to some destination. These techniques are occasionally useful, and others will be discussed in Chapter 8. It is sometimes necessary to extend a byte-length number to word or doubleword length, or a word length number to four bytes; instructions for doing this are covered in Section 4.4.
Suppose that you have source and destination locations declared as
source DWORD 4 DUP(?) dest DWORD 4 DUP(?)
and that you want to copy all four doublewords from the source to the destination. One way to do this is with four instructions
mov dest, source ; copy first doubleword mov dest+4, source+4 ; copy second doubleword mov dest+8, source+8 ; copy third doubleword mov dest+12, source+12 ; copy fourth doubleword
An address like source+4 refers to the location four bytes (one doubleword) after the address of source. Since the four doublewords reserved at source are contiguous in memory, source+4 refers to the second doubleword. This code clearly would not be space efficient if you needed to copy 40 or 400 doublewords. In Chapter 5 you will learn how to set up a loop to copy multiple objects and in Chapter 7 you will learn how to use string operations to copy large blocks of data.
The 80×86 has a very useful xchg instruction that exchanges data in one location with data in another location. It accomplishes in a single instruction the operation that often requires three high-level language instructions. Suppose Value1 and Value2 are being exchanged. In a design or a high-level language, this might be done using
Temp := Value1; { swap Value1 and Value2 }
Value1 := Value2;
Value2 := Temp;
Assuming that Value1 is stored in the EAX register and Value2 is stored in the EBX register, the above swap can be coded as
xchg eax, ebx ; swap Value1 and Value2
Instead of using the xchg instruction, one could code
mov ecx, eax ; swap Value1 and Value2 mov eax, ebx mov ebx, ecx
However, each of these mov instructions takes one clock cycle and two bytes for a total of three clock cycles and six bytes of code; the xchg instruction requires only two bytes and two clock cycles (on a Pentium). In addition, it is much easier to write one instruction than three, and the resulting code is easier to understand.
Figure 4.4 lists the various forms of the xchg instruction. Since 16-bit and 32-bit instructions are the same, distinguished by a prefix byte, they are shown together in the table. Although the table does not show it, the first operand can be a memory operand when the second operand is a register; the assembler effectively reverses the order of the operands and uses the form shown in the table.
The xchg instructions illustrate again that the accumulator sometimes plays a special role in a computer's architecture. There are special instructions for swapping another register with the accumulator that are both faster than and require fewer bytes than the corresponding general-use register-to-register exchanges. These instructions can be also be used with the accumulator as the second operand.
|
Clock Cycles |
||||||
|---|---|---|---|---|---|---|
|
Operand 1 |
Operand 2 |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
register 8 |
register 8 |
3 |
3 |
3 |
2 |
86 |
|
register 8 |
memory byte |
5 |
5 |
3 |
2-7 |
86 |
|
EAX/AX |
register 32/16 |
3 |
3 |
2 |
1 |
|
|
ECX/CX |
91 |
|||||
|
EDX/DX |
92 |
|||||
|
EBX/BX |
93 |
|||||
|
ESP/SP |
94 |
|||||
|
EBP/BP |
95 |
|||||
|
ESI/SI |
96 |
|||||
|
EDI/DI |
97 |
|||||
|
register 32/16 |
register 32/16 |
3 |
3 |
3 |
2 |
87 |
|
register 32/16 |
memory 32/16 |
5 |
5 |
3 |
2-7 |
87 |
Figure 4.4: xchg instructions
Note that you cannot use an xchg instruction to swap two memory operands. In general, 80×86 instructions do not allow two memory operands.
Like mov instructions, xchg instructions do not alter any status flag; that is, after execution of an xchg instruction, the contents of the EFLAGS register remains the same as it was before execution of the instruction.
Exercises 4.1
- For each part of this problem, assume the "before" values when the given mov instruction is executed. Give the requested "after" values.
Before
Instruction
After
(a)
BX: FF 75
CX: 01 A2mov bx, cx
BX, CX
(b)
AX: 01 A2
mov ax, 100
AX
(c)
EDX: FF 75 4C 2E
Value: DWORD −1mov edx, Value
EDX, Value
(d)
AX: 01 4B
mov ah, 0
AX
(e)
AL: 64
mov al, -1
AL
(f)
EBX: 00 00 3A 4C
Value: DWORD ?mov Value, ebx
EBX, Value
(g)
ECX: 00 00 00 00
mov ecx, 128
ECX
- Give the opcode for each instruction in Exercise 1.
- For each part of this problem, assume the "before" values when the given xchg instruction is executed. Give the requested "after" values.
Before
Instruction
After
(a)
BX: FF 75
CX: 01 A2xchg bx, cx
BX, CX
(b)
AX: 01 A2
Temp: WORD −1xchg Temp, ax
AX, Temp
(c)
DX: FF 75
xchg dl, dh
DX
(d)
AX: 01 4B
BX: 5C D9xchg ah, bl
AX, BX
(e)
EAX: 12 BC 9A 78
EDX: 56 DE 34 F0xchg eax, edx
EAX, EDX
- Give the opcode for each instruction in Exercise 3.
- Suppose that number references a doubleword in the data segment of a program, and you wish to swap the contents of that word with the contents of the EDX register. Two possible methods are
xchg edx, number
and
mov eax, edx mov edx, number mov number, eax
- What is the total number of clock cycles and the total number of bytes required by each of these methods assuming you are using a Pentium computer? Assuming you are using a 80386 computer?
- How many nanoseconds would it take to execute each set of instructions using a 166 MHz Pentium computer? Using a 20 MHz 80386 computer?
- What difference would it make in the answers to (a) if the EBX register rather than the accumulator EAX were used in the "three-move" method?
- Note that xchg cannot swap two words in memory. Write a sequence of mov and/or xchg instructions to swap doublewords stored at Value1 and Value2. Assume that any register 32 you want to use is available, and make your code as time efficient and space efficient as possible.
- How many clock cycles and how many bytes are required for the following instruction? Assume a Pentium system.
mov dx, [ebx] ; copy table entry
Integer Addition and Subtraction Instructions
The Intel 80×86 microprocessor has add and sub instructions to perform addition and subtraction using byte, word, or doubleword length operands. The operands can be interpreted as unsigned numbers or 2’s complement signed numbers. The 80×86 architecture also has inc and dec instructions to increment (add 1 to) and decrement (subtract 1 from) a single operand, and a neg instruction that negates (takes the 2’s complement of) a single operand.
One difference between the instructions covered in this section and the mov and xchg instructions of Section 4.1 is that add, sub, inc, dec, and neg instructions all update flags in the EFLAGS register. The SF, ZF, OF, PF, and AF flags are set according to the value of the result of the operation. For example, if the result is negative, then the sign flag SF will be set to one; if the result is zero, then the zero flag ZF will be set to one. The carry flag CF is also given a value by each of these instructions except inc and dec.
Each add instruction has the form
add destination, source
When executed, the integer at source is added to the integer at destination and the sum replaces the old value at destination. The sub instructions all have the form
sub destination, source
When a sub instruction is executed, the integer at source is subtracted from the integer at destination and the difference replaces the old value at destination. For subtraction, it is important to remember that the difference calculated is
destination - source
or "operand 1 minus operand 2." With both add and sub instructions the source (second) operand is unchanged. Here are some examples showing how these instructions function at execution time.

Addition and subtraction instructions set the sign flag SF to be the same as the high-order bit of the result. Thus, when these instructions are used to add or subtract 2’s complement integers, SF=1 indicates a negative result. The zero flag ZF is 1 if the result is zero, and 0 if the result is nonzero. The carry flag CF records a carry out of the high order bit with addition or a borrow with subtraction. The overflow flag OF records overflow, as discussed in Chapter 2.
One reason that 2’s complement form is used to represent signed numbers is that it does not require special hardware for addition or subtraction; the same circuits can be used to add unsigned numbers and 2’s complement numbers. The flag values have different interpretations, though, depending on the operand type. For instance, if you add two large unsigned numbers and the high order bit of the result is 1, then SF will be set to 1, but this does not indicate a negative result, only a relatively large sum. For an add with unsigned operands, CF=1 would indicate that the result was too large to store in the destination, but with signed operands, OF=1 would indicate a size error.
Figure 4.5 gives information for both addition and subtraction instructions. For each add there is a corresponding sub instruction with exactly the same operand types, number of clock cycles, and number of bytes of object code, so that it is redundant to make separate tables for add and sub instructions.
|
Clock Cycles |
Opcode |
||||||
|---|---|---|---|---|---|---|---|
|
Destination Operand |
Source Operand |
386 |
486 |
Pentium |
Number of Bytes |
add |
sub |
|
register 8 |
immediate 8 |
2 |
1 |
1 |
3 |
80 |
80 |
|
register 16 |
immediate 8 |
2 |
1 |
1 |
3 |
83 |
83 |
|
register 32 |
immediate 8 |
2 |
1 |
1 |
3 |
83 |
83 |
|
register 16 |
immediate 16 |
2 |
1 |
1 |
4 |
81 |
81 |
|
register 32 |
immediate 32 |
2 |
1 |
1 |
6 |
81 |
81 |
|
AL |
immediate 8 |
2 |
1 |
1 |
2 |
04 |
2C |
|
AX |
immediate 16 |
2 |
1 |
1 |
3 |
05 |
2D |
|
EAX |
immediate 32 |
2 |
1 |
1 |
5 |
05 |
2D |
|
memory byte |
immediate 8 |
7 |
3 |
3 |
3+ |
80 |
80 |
|
memory word |
immediate 8 |
7 |
3 |
3 |
3+ |
83 |
83 |
|
memory doubleword |
immediate 8 |
7 |
3 |
3 |
3+ |
83 |
83 |
|
memory word |
immediate 16 |
7 |
3 |
3 |
4+ |
81 |
81 |
|
memory doubleword |
immediate 32 |
7 |
3 |
3 |
6+ |
81 |
81 |
|
register 8 |
register 8 |
2 |
1 |
1 |
2 |
02 |
2A |
|
register 16 |
register 16 |
2 |
1 |
1 |
2 |
03 |
2B |
|
register 32 |
register 32 |
2 |
1 |
1 |
2 |
03 |
2B |
|
register 8 |
memory byte |
6 |
2 |
2 |
2+ |
02 |
2A |
|
register 16 |
memory word |
6 |
2 |
2 |
2+ |
03 |
2B |
|
register 32 |
memory doubleword |
6 |
2 |
2 |
2+ |
03 |
2B |
|
memory byte |
register 8 |
7 |
3 |
3 |
2+ |
00 |
28 |
|
memory word |
register 16 |
7 |
3 |
3 |
2+ |
01 |
29 |
|
memory doubleword |
register 32 |
7 |
3 |
3 |
2+ |
01 |
29 |
Figure 4.5: add and sub instructions
Figure 4.6 makes it easy to see that addition or subtraction operands are the fastest when both operands are in registers and the slowest when the destination operand is in memory. It is interesting to note that it is faster to add an operand in memory to the contents of a register than to add the value in a register to a memory operand; this is true since memory must be accessed twice in the latter case, once to get the first addend and once to store the sum. With the 80×86, only one operand can be in memory. Many computer architectures do not have instructions for arithmetic when the destination is a memory operand. Some other processors allow two memory operands for arithmetic operations.
|
Clock Cycles |
Opcode |
|||||
|---|---|---|---|---|---|---|
|
Destination Operand |
386 |
486 |
Pentium |
Number of Bytes |
inc |
dec |
|
register 8 |
2 |
1 |
1 |
2 |
FE |
FE |
|
register 16 |
2 |
1 |
1 |
1 |
||
|
AX |
40 |
48 |
||||
|
CX |
41 |
49 |
||||
|
DX |
42 |
4A |
||||
|
BX |
43 |
4B |
||||
|
SP |
44 |
4C |
||||
|
BP |
45 |
4D |
||||
|
SI |
46 |
4E |
||||
|
DI |
47 |
4F |
||||
|
register 32 |
2 |
1 |
1 |
1 |
||
|
EAX |
40 |
48 |
||||
|
ECX |
41 |
49 |
||||
|
EDX |
42 |
4A |
||||
|
EBX |
43 |
4B |
||||
|
ESP |
44 |
4C |
||||
|
EBP |
45 |
4D |
||||
|
ESI |
46 |
4E |
||||
|
EDI |
47 |
4F |
||||
|
memory byte |
6 |
3 |
3 |
2+ |
FE |
FE |
|
memory word |
6 |
3 |
3 |
2+ |
FF |
FF |
|
memory doubleword |
6 |
3 |
3 |
2+ |
FF |
FF |
Figure 4.6: inc and dec instructions
With add and sub, the accumulator again has special instructions, this time when EAX, AX, or AL is the destination and the source is immediate. These instructions are not any faster than the other immediate-to-register instructions but do take one less byte of object code.
The total number of object code bytes for instructions with "+" entries in Fig. 4.6 can be calculated once you know the memory operand type. In particular, for direct mode, you add four bytes for the 32-bit address. For register indirect mode, no additional byte is required.
Notice that an immediate source can be a single byte even when the destination is a word or doubleword. Since immediate operands are often small, this makes the object code more compact. Byte-size operands are sign-extended to word or doubleword size at run time before the addition or subtraction operation. If the original operand is negative (viewed as 2’s complement number), then it is extended with one or three FF bytes to get the corresponding word or doubleword-length value. A non-negative operand is simply extended with one or three 00 bytes. In both cases this is equivalent to copying the original sign bit to the high order 8 or 24 bit positions.
It may be surprising that some add and sub instructions have the same opcode. In such cases, one of the fields in the second instruction byte distinguishes between addition and subtraction. In fact, these same opcodes are used for additional instructions that are covered later in this book.
The inc (increment) and dec (decrement) instructions are special-purpose addition and subtraction instructions, always using 1 as an implied source. They have the forms
inc destination
and
dec destination
Like the add and sub instructions, these instructions are paired with respect to allowable operand types, clock cycles, and bytes of object code. They are summarized together in Fig. 4.6.
The inc and dec instructions treat the value of the destination operand as an unsigned integer. They affect the OF, SF, and ZF flags just like addition or subtraction of one, but they do not change the carry flag CF. Here are examples showing the execution of a few increment and decrement instructions:

The inc and dec instructions are especially useful for incrementing and decrementing counters. They sometimes take fewer bytes of code and execute in fewer clock cycles than corresponding addition or subtraction instructions. For example, the instructions
add cx, 1 ; increment loop counter
and
inc cx ; increment loop counter
are functionally equivalent. The add instruction requires three bytes (three bytes instead of four since the immediate operand will fit in one byte), while the inc instruction requires one byte. Either executes in two clock cycles on an 80386 machine or in one clock cycle on an 80486 or Pentium, so execution times are identical.
In Fig. 4.6, note the fast, single-byte inc and dec instructions for word or doubleword-size operands stored in registers. A register is the best place to keep a counter, if one can be reserved for this purpose.
A neg instruction negates, or finds the 2’s complement of, its single operand. When a positive value is negated the result is negative; a negative value will become positive. Zero remains zero. Each neg instruction has the form
neg destination
Figure 4.7 shows allowable operands for neg instructions.
|
Clock Cycles |
|||||
|---|---|---|---|---|---|
|
Destination Operand |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
register 8 |
2 |
1 |
1 |
2 |
F6 |
|
register 16 |
2 |
1 |
1 |
2 |
F7 |
|
register 32 |
2 |
1 |
1 |
2 |
F7 |
|
memory byte |
6 |
3 |
3 |
2+ |
F6 |
|
memory word |
6 |
3 |
3 |
2+ |
F7 |
|
memory doubleword |
6 |
3 |
3 |
2+ |
F7 |
Figure 4.7: neg instructions
Following are four examples illustrating how the neg instructions operate. In each case the "after" value is the 2’s complement of the "before" value.

This section ends with an example of a complete, if unexciting, program that uses these new instructions. The program inputs values for three numbers, x, y and z, evaluates the expression (−x + y −2z + 1) and displays the result. The design implemented is
- prompt for and input value for x;
- convert × from ASCII to 2’s complement form;
- expression := x;
- prompt for and input value for y;
- convert y from ASCII to 2’s complement form;
- add y to expression, giving × + y;
- prompt for and input value for z;
- convert z from ASCII to 2’s complement form;
- calculate 2*z as (z + z);
- subtract 2*z from expression, giving × + y −2*z;
- add 1 to expression, giving × + y −2*z + 1;
- negate expression, giving (−x + y −2*z + 1);
- convert the result from 2’s complement to ASCII;
- display the result;
To write an assembly language program, you need to plan how registers and memory will be used. In this program the values of x, y, and z are not needed after they are incorporated into the expression. Therefore they are not stored in memory. We will assume that the numbers are not very large, so that values can be stored in words. A logical place to keep the expression value would be the accumulator AX since some operations are faster with it, but this choice is impossible since the atoi macro always uses AX as its destination. This leaves the general registers BX, CX, and DX; this program will use DX. It is very easy to run out of registers when designing assembly language programs. Memory must often be used for values even though operations are slower. Sometimes values must be moved back and forth between registers and memory.
Figure 4.8 shows the source program listing. This program follows the same general pattern of the example in Fig. 3.1. In the prompts, note the use of cr,Lf,Lf to skip to a new line and to leave an extra blank line; it is not necessary to put in a second cr since the cursor will already be at the beginning of the new line after one carriage return character is displayed. The value of 2*z is found by adding z to itself; multiplication will be covered in the next section, but it is more efficient to compute 2*z by addition. Finally, note that the comments in this program do not simply repeat the instruction mnemonics; they help the human reader figure out what is really going on.
; program to input values for x, y and z ; and evaluate the expression - (x + y - 2z + 1) ; author: R. Detmer ; date: revised 8/97 .386 .MODEL FLAT ExitProcess PROTO NEAR32 stdcall, dwExitCode:DWORD include io.h ; header file for input/output cr equ 0dh ; carriage return character Lf equ 0ah ; line feed .STACK 4096 ; reserve 4096-byte stack .DATA ; reserve storage for data Prompt1 BYTE "This program will evaluate the expression",cr,Lf,Lf BYTE " - (x + y - 2z + 1)",cr,Lf,Lf BYTE "for your choice of integer values.",cr,Lf,Lf BYTE "Enter value for x: ",0 Prompt2 BYTE "Enter value for y: ",0 Prompt3 BYTE "Enter value for z: ",0 Value BYTE 16 DUP (?) Answer BYTE cr,Lf,"The result is " Result BYTE 6 DUP (?) BYTE cr,Lf,0 .CODE ; start of main program code _start: output Prompt1 ; prompt for x input Value,16 ; read ASCII characters atoi Value ; convert to integer mov dx,ax ; x output Prompt2 ; prompt for y input Value,16 ; read ASCII characters atoi Value ; convert to integer add dx,ax ; x + y output Prompt3 ; prompt for z input Value,16 ; read ASCII characters atoi Value ; convert to integer add ax,ax ; 2*z sub dx,ax ; x + y - 2*z inc dx ; x + y - 2*z + 1 neg dx ; - (x + y - 2*z + 1) itoa Result,dx ; convert to ASCII characters output Answer ; output label and result INVOKE ExitProcess, 0 ; exit with return code 0 PUBLIC _start ; make entry point public END ; end of source code
Figure 4.8: Program to evaluate − (x + y − 2z + 1)
Figure 4.9 illustrates a sample run of this program. As in the previous example, user input is underlined.
This program will evaluate the expression - (x + y - 2z + 1) for your choice of integer values. Enter value for x: 10 Enter value for y: 3 Enter value for z: 5 The result is -4
Figure 4.9: Sample run of program
Exercises 4.2
- For each instruction, give the opcode, the number of bytes of object code, and the number of clock cycles required for execution on a Pentium system. Assume that Value references a word in memory and that Double references a doubleword.
(a)
add ax,Value
(b)
sub Value,ax
(c)
sub eax,10
(d)
add Double,10
(e)
add eax,[ebx]
(f)
sub [ebx],eax
(g)
sub dl,ch
(h)
add bl,5
(i)
inc bx
(j)
dec al
(k)
dec Double
(l)
inc BYTE PTR [esi]
(m)
neg eax
(n)
neg bh
(o)
neg Double
(p)
neg WORD PTR [ebx]
- For each part of this problem, assume the "before" values when the given instruction is executed. Give the requested "after" values.
Before
Instruction
After
(a)
EBX: FF FF FF 75
ECX: 00 00 01 A2add ebx,ecx
EBX, ECX, SF, ZF, CF, OF
(b)
EBX: FF FF FF 75
ECX: 00 00 01 A2sub ebx,ecx
EBX, ECX, SF, ZF, CF, OF
(c)
BX: FF 75
CX: 01 A2sub cx,bx
BX, CX, SF, ZF, CF, OF
(d)
DX: 01 4B
add dx,40h
DX, SF, ZF, CF, OF
(e)
EAX: 00 00 00 64
sub eax,100
EAX, SF, ZF, CF, OF
(f)
AX: 0A 20
word at Value, word at Value: FF 20add ax,Value
AX, SF, ZF, CF, OF
(g)
AX: 0A 20
word at Value, word at Value: FF 20sub Value,ax
AX, SF, ZF, CF, OF
(h)
CX: 03 1A
inc cx
CX, SF, ZF
(i)
EAX: 00 00 00 01
dec eax
EAX, SF, ZF
(j)
word at Count: 00 99
inc Count
word at Count, SF, ZF
(k)
word at Count: 00 99
dec count
word at Count, SF, ZF
(l)
EBX: FF FF FF FF
neg ebx
EBX, SF, ZF
(m)
CL: 5F
neg cl
CL, SF, ZF
(n)
word at Value: FB 3C
neg Value
word at Value, SF, ZF
Programming Exercises 4.2
For complete programs, prompts for input must make it clear what is to be entered, and output must be appropriately labeled.
- Write a complete 80×86 assembly language program to prompt for values of x, y, and z and display the value of the expression x −2y + 4z. Allow for 16-bit integer values.
- Write a complete 80×86 assembly language program to prompt for values of x, y, and z and display the value of the expression 2(−x + y−1) + z. Allow for 32-bit integer values.
- Write a complete 80×86 assembly language program to prompt for the length and width of a rectangle and to display its perimeter (2*length + 2*width).
Multiplication Instructions
The 80×86 architecture has two multiplication instruction mnemonics. Any imul instruction treats its operands as signed numbers; the sign of the product is determined by the usual rules for multiplying signed numbers. A mul instruction treats its operands as unsigned binary numbers; the product is also unsigned. If only non-negative numbers are to be multiplied, mul should usually be chosen instead of imul since it is a little faster.
There are fewer variants of mul than of imul, so we consider it first. The mul instruction has a single operand; its format is
mul source
The source operand may be byte, word, or doubleword-length, and it may be in a register or in memory. The location of the other number to be multiplied is always the accumulator-AL for a byte source, AX for a word source, and EAX for a doubleword source. If source has byte length, then it is multiplied by the byte in AL; the product is 16 bits long, with a destination of the AX register. If source has word length, then it is multiplied by the word in AX; the product is 32 bits long, with its low order 16 bits going to the AX register and its high order 16 bits going to the DX register. If source is a doubleword, then it is multiplied by the doubleword in EAX; the product is 64 bits long, with its low order 32 bits in the EAX register and its high order 32 bits in the EDX register. For byte multiplication, the original value in AX is replaced. For word multiplication, the original values in AX and DX are both wiped out. Similarly, for doubleword multiplication the values in EAX and EDX are replaced by the product. In each case the source operand is unchanged unless it is half of the destination location.
At first glance, it may seem strange that the product is twice the length of its two factors. However, this also occurs in ordinary decimal multiplication; if, for example, two four-digit numbers are multiplied, the product will be seven or eight digits long. Computers that have multiplication operations often put the product in double-length locations so that there is no danger that the destination location will be too small.
Even when provision is made for double-length products, it is useful to be able to tell whether the product is the same size as the source; that is, if the high-order half is zero. With mul instructions, the carry flag CF and overflow flag OF are set to 1 if the high order half of the product is not zero, but are cleared to 0 if the high order half of the product is zero. These are the only meaningful flag values following multiplication operations; previously set values of AF, PF, SF, and ZF flags may be destroyed. In Chapter 5, instructions checking flag values will be covered; it is possible to check that the high order half of the product can be safely ignored.
Figure 4.10 summarizes the allowable operand types for mul instructions. No immediate operand is allowed in a mul. Note the number of clock cycles required is appreciably larger than for addition or subtraction instructions. The actual number of clock cycles for the 80386 and 80486 depends on the numbers being multiplied.
|
Clock Cycles |
|||||
|---|---|---|---|---|---|
|
Destination Operand |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
register 8 |
9-14 |
13-18 |
11 |
2 |
F6 |
|
register 16 |
9-22 |
13-26 |
11 |
2 |
F7 |
|
register 32 |
9-38 |
13-42 |
10 |
2 |
F7 |
|
memory byte |
12-17 |
13-18 |
11 |
2+ |
F6 |
|
memory word |
12-25 |
13-26 |
11 |
2+ |
F7 |
|
memory doubleword |
12-41 |
13-42 |
10 |
2+ |
F7 |
Figure 4.10: mul instructions
Here are some examples to illustrate how the mul instructions work.
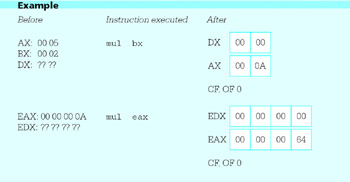

The first example shows multiplication of words in AX and BX. The contents of DX are not used in the multiplication but are replaced by the high-order 16 bits of the 32-bit product 0000000A. The carry and overflow flags are cleared to 0 since DX contains 0000. The second example shows multiplication of EAX by itself, illustrating that the explicit source for the multiplication can be the same as the other implicit factor. The final example shows multiplication of the byte in AL by a byte at Factor in memory with value equivalent to the unsigned number 25510. The product is the unsigned 16-bit number 04 FB, and since the high-order half is not zero, both CF and OF are set to 1.
The signed multiplication instructions use mnemonic imul. There are three formats, each with a different number of operands. The first format is
imul source
the same as for mul, with source containing one factor and the accumulator the other. Again, the source operand cannot be immediate. The destination is AX, DX:AX, or EDX:EAX, depending on the size of the source operand. The carry and overflow flags are set to 1 if the bits in the high-order half are significant, and cleared to 0 otherwise. Notice the high-order half may contain all 1 bits for a negative product. Single-operand imul instructions are summarized in Fig. 4.11. Notice that this table is identical to Fig. 4.10. Even the opcodes are the same for mul and single-operand imul instructions, with a field in the second byte of the instruction distinguishing the two.
|
Clock Cycles |
|||||
|---|---|---|---|---|---|
|
Destination Operand |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
register 8 |
9-14 |
13-18 |
11 |
2 |
F6 |
|
register 16 |
9-22 |
13-26 |
11 |
2 |
F7 |
|
register 32 |
9-38 |
13-42 |
10 |
2 |
F7 |
|
memory byte |
12-17 |
13-18 |
11 |
2+ |
F6 |
|
memory word |
12-25 |
13-26 |
11 |
2+ |
F7 |
|
memory doubleword |
12-41 |
13-42 |
10 |
2+ |
F7 |
Figure 4.11: imul instructions (single-operand format)
The second imul format is
imul register, source
Here the source operand can be in a register, in memory, or immediate. The other factor is in the register, which also serves as the destination. Operands must be words or doublewords, not bytes. The product must "fit" in same size as the factors; if it does, CF and OF are cleared to 0, if not they are set to 1.
Figure 4.12 summarizes two-operand imul instructions. Note that some of these instructions have two byte long opcodes. Immediate operands can be either the size of the destination register or a single byte. Single-byte operands are signextended before multiplication-that is, the sign bit is copied to leading bit positions, giving a 16 or 32-bit value that represents the same signed integer as the original 8-bit operand.
|
Clock Cycles |
||||||
|---|---|---|---|---|---|---|
|
Operand 1 |
Operand 2 |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
register 16 |
register 16 |
9-22 |
13-26 |
11 |
3 |
0F AF |
|
register 32 |
register 32 |
9-38 |
13-42 |
10 |
3 |
0F AF |
|
register 16 |
memory word |
12-25 |
13-26 |
11 |
3 + |
0F AF |
|
register 32 |
memory doubleword |
12-41 |
13-42 |
10 |
3 + |
0F AF |
|
register 16 |
immediate byte |
9-14 |
13-18 |
11 |
3 |
6B |
|
register 16 |
immediate word |
9-22 |
13-26 |
11 |
4 |
69 |
|
register 32 |
immediate byte |
9-14 |
13-18 |
11 |
3 |
6B |
|
register 32 |
immediate doubleword |
9-38 |
13-42 |
10 |
6 |
69 |
Figure 4.12: imul instructions (two-operand format)
The third imul format is
imul register, source, immediate
With this version, the first operand, a register, is only the destination for the product; the two factors are the contents of the register or memory location given by source and the immediate value. Operands register and source are the same size, both 16-bit or both 32-bit. If the product will fit in the destination register, then CF and OF are cleared to 0; if not, they are set to 1. The three-operand imul instructions are summarized in Fig. 4.13.
|
Clock Cycles |
|||||||
|---|---|---|---|---|---|---|---|
|
Register Destination |
Source |
Immediate Operand |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
register 16 |
register 16 |
byte |
9-14 |
13-18 |
10 |
3 |
6B |
|
register 16 |
register 16 |
word |
9-22 |
13-26 |
10 |
4 |
69 |
|
register 16 |
memory 16 |
byte |
12-17 |
13-18 |
10 |
3+ |
6B |
|
register 16 |
memory 16 |
word |
12-25 |
13-26 |
10 |
4+ |
69 |
|
register 32 |
register 32 |
byte |
9-14 |
13-18 |
10 |
3 |
6B |
|
register 32 |
register 32 |
doubleword |
9-38 |
13-42 |
10 |
6 |
69 |
|
register 32 |
memory 32 |
byte |
12-17 |
13-18 |
10 |
3+ |
6B |
|
register 32 |
memory 32 |
doubleword |
12-41 |
13-42 |
10 |
6+ |
69 |
Figure 4.13: imul Instructions (three-operand format)
Some examples will help show how the imul instructions work.


The first two examples are the single-operand format and the products are twice the length of the operands. The first example shows words in AX (the implied operand) and BX being multiplied, with the result in DX:AX. The second example shows 5 in AL being multiplied by −1 in the memory byte at Factor, giving a word-size product equivalent to −5 in AX. The third example shows the two-operand format, with 10 in EBX multiplied by the immediate operand 10, and the result of 100 in EBX. In the fourth example, two negative numbers are multiplied, giving a positive result. In the last example, the product is 22F15016, too large to fit in BX. The flags CF and OF are set to 1 to indicate that the result was too large, and the low-order digits are saved in BX.
Earlier, the discussion with the example program in Fig. 4.8 stated that it was faster to calculate 2z by adding z to itself than by using a multiplication instruction. In that situation, z was in the AX register, so
add ax, ax ; compute 2z
did the job. This instruction is two bytes long, and on an 80486 or Pentium system takes one clock cycle. To do the same task using multiplication, you can code
imul ax, 2 ; compute 2z
This instruction (from Fig. 4.12) is three bytes long since the immediate operand 2 is short enough to fit in a single byte; it takes 13-18 clock cycles on an 80486 or 10 clock cycles on a Pentium, much longer than the addition instruction.
This section concludes with an example of a program that will input the length and width of a rectangle and calculate its area (length*width). (Admittedly, this is a job much better suited for a hand calculator than for a computer program in assembly language or any other language.) Figure 4.14 shows the source code for the program. Note that the program uses mul rather than imul for finding the product; lengths and widths are positive numbers. Interesting errors occur in this program if a negative length or width is entered, or if a large width and length (say 200 and 300) are entered. Why? Such errors are unfortunately common in software.
; program to find the area of a rectangle ; author: R. Detmer ; date: revised 9/97 .386 .MODEL FLAT ExitProcess PROTO NEAR32 stdcall, dwExitCode:DWORD INCLUDE io.h cr EQU 0dh ; carriage return character LF EQU 0ah ; linefeed character .STACK 4096 ; reserve 4096-byte stack .DATA ; reserve storage for data prompt1 BYTE "This program will find the area of a rectangle",cr,Lf,Lf BYTE "Width of rectangle? ",0 prompt2 BYTE "Length of rectangle? ",0 value BYTE 16 DUP (?) answer BYTE cr,Lf,"The area of the rectangle is " area BYTE 11 DUP (?) BYTE cr,Lf,0 .CODE ;start of main program code _start: Prompt: output prompt1 ;prompt for width input value,16 ; read ASCII characters atod value ; convert to integer mov ebx,eax ; width output prompt2 ; prompt for length input value,16 ; read ASCII characters atod value ; convert to integer mul ebx ; length * width dtoa area,eax ; convert to ASCII characters output answer ; output label and result INVOKE ExitProcess, 0 ; exit with return code 0 PUBLIC _start ; make entry point public END
Figure 4.14: Program to find the area of a rectangle
As you have seen in this section, the 80×86 architecture includes multiplication instructions in three formats. You may have noted that the destination of the product cannot be a memory operand. This may sound restrictive, but some processors have even greater limitations. In fact, most 8-bit microprocessors, including the Intel 8080, had no multiplication instruction; any multiplication had to be done using a software routine.
Exercises 4.3
- For each part of this problem, assume the "before" values when the given instruction is executed. Give the requested "after" values.
Before
Instruction
After
(a)
EAX: FF FF FF E4
EBX: 00 00 00 02mul ebx
EAX, EDX, CF, OF
(b)
AX: FF E4
word at Value: FF 3Amul Value
AX, DX, CF, OF
(c)
AX: FF FF
mul ax
AX, DX, CF, OF
(d)
AL: 0F
BH: 4Cmul bh
AX, CF, OF
(e)
AL: F0
BH: C4mul bh
AX, CF, OF
(f)
AX: 00 17
CX: 00 B2imul cx
AX, DX, CF, OF
(g)
EAX: FF FF FF E4
EBX: 00 00 04 C2imul ebx
EAX, EDX, CF, OF
(h)
AX: FF E4
word at Value: FF 3Aimul Value
AX, DX, CF, OF
(i)
EAX: FF FF FF FF
imul eax
EAX, EDX, CF, OF
(j)
AL: 0F
BH: 4Cimul bh
AX, CF, OF
(k)
AL: F0
BH: C4imul bh
AX, CF, OF
- Give the opcode for each instruction in Exercise 1.
- For each part of this problem, assume the "before" values when the given instruction is executed. Give the requested "after" values.
Before
Instruction
After
(a)
BX: 00 17
CX: 00 B2imul bx,cx
BX, CF, OF
(b)
EAX: FF FF FF E4
EBX: 00 00 04 C2imul eax,ebx
EAX, CF, OF
(c)
AX: 0F B2
imul ax, 15
AX, CF, OF
(d)
ECX: 00 00 7C E4
doubleword at Mult:
00 00 65 EDimul ecx,Mult
ECX, CF, OF
(e)
DX: 7C E4
BX: 49 30imul dx,bx
DX, CF, OF
(f)
DX: 0F E4
word at Value: 04 C2imul dx,Value
DX, CF, OF
(g)
EBX: 00 00 04 C2
imul ebx,-10
EBX, CF, OF
(h)
ECX: FF FF FF E4
imul ebx,ecx,5
EBX, CF, OF
(i)
DX: 00 64
imul ax,dx,10
AX, CF, OF
- Give the opcode for each instruction in Exercise 3.
- Suppose that the value for x is in the AX register and you need the value of 5x in AX. Compare the number of clock cycles for execution on a Pentium system and the number of bytes of object code for each of the following schemes.
mov bx,ax ; copy value of x add ax,ax ; x + x gives 2x add ax,ax ; 2x + 2x gives 4x add ax,bx ; 4x + x gives 5x
and
imul ax,5 ; 5x
- Suppose you need to evaluate the polynomial
p(x) = 5x3 7x2 + 3x −10
for some value of x. If this is done in the obvious way, as
5*x*x*x −7*x*x + 3*x −10
there are six multiplications and three additions/subtractions. An equivalent form, based on Horner's scheme for evaluation of polynomials, is
((5*x −7)*x + 3)*x −10
This has only three multiplications.
Suppose that the value of x is in the EAX register.
- Write 80×86 assembly language statements that will evaluate p(x) the "obvious" way, putting the result in EAX.
- Write 80×86 assembly language statements that will evaluate p(x) using Horner's scheme, again putting the result in EAX.
- Assuming a Pentium system, compare the number of clock cycles for execution and the number of bytes of object code required for the code fragments in (a) and in (b) above.
- The 80×86 architecture has distinct instructions for multiplication of signed and unsigned numbers. It does not have separate instructions for addition of signed and unsigned numbers. Why are different instructions needed for multiplication but not for addition?
Programming Exercises 4.3
- Write a complete 80×86 assembly language program to prompt for the length, width, and height of a box and to display its volume (length * width * height).
- Write a complete 80×86 assembly language program to prompt for the length, width, and height of a box and to display its surface area
- 2*(length*width + length*height + width*height).
- Suppose that someone has a certain number of coins (pennies, nickels, dimes, quarters, fifty-cent pieces, and dollar coins) and wants to know the total value of the coins, as well as how many coins there are. Write a program to help. Specifically, follow the design below.
- prompt for and input the number of pennies;
- total := number of pennies;
- numberOfCoins := number of pennies;
- prompt for and input the number of nickels;
- total := total + 5 * number of nickels;
- add number of nickels to numberOfCoins;
- prompt for and input the number of dimes;
- total := total + 10 * number of dimes;
- add number of dimes to numberOfCoins;
- prompt for and input the number of quarters;
- total := total + 25 * number of quarters;
- add number of quarters to numberOfCoins;
- prompt for and input the number of fifty-cent pieces;
- total := total + 50 * number of fifty-cent pieces;
- add number of fifty-cent pieces to numberOfCoins;
- prompt for and input the number of dollars;
- total := total + 100 * number of dollars;
- add number of dollars to numberOfCoins;
- display "There are", numberOfCoins, "coins worth";
- display total div 100, "dollars and", total mod 100, "cents";
Note that you are displaying dollars and cents for the total. Assume that all values will fit in doublewords.
Division Instructions
The Intel 80×86 instructions for division parallel those of the single-operand multiplication instructions; idiv is for division of signed 2's complement integers and div is for division of unsigned integers. Recall that the single-operand multiplication instructions start with a multiplier and multiplicand and produce a double-length product. Division instructions start with a double-length dividend and a single-length divisor, and produce a single-length quotient and a single-length remainder. The 80×86 has instructions that can be used to produce a double-length dividend prior to division.
The division instructions have formats
idiv source
and
div source
The source operand identifies the divisor. The divisor can be in a register or memory, but not immediate. Both div and idiv use an implicit dividend (the operand you are dividing into). If source is byte length, then the double-length dividend is word size and is assumed to be in the AX register. If source is word length, then the dividend is a doubleword and is assumed to have its low order 16 bits in the AX register and its high order 16 bits in the DX register. If source is doubleword length, then the dividend is a quadword (64 bits) and is assumed to have its low order 32 bits in the EAX register and its high order 32 bits in the EDX register.
The table in Fig. 4.15 summarizes the locations of the dividend, divisor, quotient, and remainder for 80×86 division instructions.
|
source (divisor) size |
other operand (dividend) |
quotient |
remainder |
|---|---|---|---|
|
byte |
AX |
AL |
AH |
|
word |
DX:AX |
AX |
DX |
|
doubleword |
EDX:EAX |
EAX |
EDX |
Figure 4.15: Operands and results for 80×86 division instructions
The source operand (the divisor) is not changed by a division instruction. After a word in AX is divided by a byte length divisor, the quotient will be in the AL register half and the remainder will be in the AH register half. After a doubleword in DX and AX is divided by a word length divisor, the quotient will be in the AX register and the remainder will be in the DX register. After a quadword in EDX and EAX is divided by a doubleword length divisor, the quotient will be in the EAX register and the remainder will be in the EDX register.
For all division operations, the dividend, divisor, quotient, and remainder must satisfy the equation
dividend = quotient*divisor + remainder
For unsigned div operations, the dividend, divisor, quotient, and remainder are all treated as non-negative numbers. For signed idiv operations, the sign of the quotient is determined by the signs of the dividend and divisor using the ordinary rules of signs; the sign of the remainder is always the same as the sign of the dividend.
The division instructions do not set flags to any significant values. They may destroy previously set values of AF, CF, OF, PF, SF, and ZF flags.
Some examples show how the division instructions work.

In each of these examples, the decimal number 100 is divided by 13. Since
100 = 7 * 13 + 9
the quotient is 7 and the remainder is 9. For the doubleword length divisor, the quotient is in EAX and the remainder is in EDX. For the word length divisor, the quotient is in AX and the remainder is in DX. For the byte length divisor, the quotient is in AL and the remainder is in AH.
For operations where the dividend or divisor is negative, equations analogous to the one above are
100 = (-7) * (-13) + 9 -100 = (-7) * 13 + (-9) -100 = 7* (-13) + (-9)
Note that in each case the sign of the remainder is the same as the sign of the dividend. The following examples reflect these equations for word size divisors of 13 or −13.


In the second and third examples, the dividend −100 is represented as the 32 bit number FF FF FF 9C in the DX and AX registers.
Finally, here are two examples to help illustrate the difference between signed and unsigned division.

With the signed division, −511 is divided by −32, giving a quotient of 15 and a remainder of −31. With the unsigned division, 65025 is divided by 255, giving a quotient of 255 and a remainder of 0.
With multiplication, the double length destination in each single-operand format guarantees that the product will fit in the destination location-nothing can go wrong during a single-operand multiplication operation. There can be errors during division. One obvious cause is an attempt to divide by zero. A less obvious reason is a quotient that is too large to fit in the single-length destination; if, say, 00 02 46 8A is divided by 2, the quotient 1 23 45 is too large to fit in the AX register. If an error occurs during the division operation, the 80×86 generates an exception. The routine, or interrupt handler, that services this exception may vary from system to system. Windows 95 on the author's Pentium system pops up a window with the message "This program has performed an illegal operation and will be shut down." When the Details button is pressed, it displays "TEST caused a divide error…" The 80×86 leaves the destination registers undefined following a division error.
Figure 4.16 lists the allowable operand types for idiv instructions and Fig. 4.17 lists the allowable operand types for div instructions. The only differences in the two tables are in the number of clock cycles columns; div operations are slightly faster than idiv operations.
|
Clock Cycles |
|||||
|---|---|---|---|---|---|
|
Operand |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
register 8 |
19 |
19 |
22 |
2 |
F6 |
|
register 16 |
27 |
27 |
30 |
2 |
F7 |
|
register 32 |
43 |
43 |
48 |
2 |
F7 |
|
memory byte |
22 |
20 |
22 |
2 + |
F6 |
|
memory word |
30 |
28 |
30 |
2 + |
F7 |
|
memory doubleword |
46 |
44 |
48 |
2 + |
F7 |
Figure 4.16: idiv instructions
|
Clock Cycles |
|||||
|---|---|---|---|---|---|
|
Operand |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
register 8 |
14 |
16 |
17 |
2 |
F6 |
|
register 16 |
22 |
24 |
25 |
2 |
F7 |
|
register 32 |
38 |
40 |
41 |
2 |
F7 |
|
memory byte |
17 |
16 |
17 |
2 + |
F6 |
|
memory word |
25 |
24 |
25 |
2 + |
F7 |
|
memory doubleword |
41 |
40 |
41 |
2 + |
F7 |
Figure 4.17: div instructions
When arithmetic is being done with operands of a given length, the dividend must be converted to double length before a division operation is executed. For unsigned division, a doubleword-size dividend must be converted to quadword size with leading zero bits in the EDX register. This can be accomplished many ways, two of which are
mov edx, 0
and
sub edx, edx
Similar instructions can be used to put a zero in DX prior to unsigned division by a word operand or to put a zero in AH prior to unsigned division by a byte operand.
The situation is more complicated for signed division. A positive dividend must be extended with leading 0 bits, but a negative dividend must be extended with leading 1 bits. The 80×86 has three instructions for this task. The cbw, cwd, and cdq instructions are different from the instructions covered before in that these instructions have no operands. The cbw instruction always has AL as its source and AX as its destination, cwd always has AX as its source and DX and AX as its destination, and cdq always has EAX as its source and EDX and EAX as its destination. The source register is not changed, but is extended as a signed number into AH, DX, or EDX. These instructions are summarized together in Fig. 4.18, which also includes the cwde instruction that extends the word in AX to its signed equivalent in EAX, paralleling the job that cbw does.
|
Clock Cycles |
|||||
|---|---|---|---|---|---|
|
Instruction |
386 |
486 |
Pentium |
Number of Bytes |
Opcode |
|
cbw |
3 |
3 |
3 |
1 |
98 |
|
cwd |
2 |
3 |
2 |
1 |
99 |
|
cdq |
2 |
3 |
2 |
1 |
99 |
|
cwde |
3 |
3 |
3 |
1 |
98 |
Figure 4.18: cbw and cwd instructions
The cbw (convert byte to word) instruction extends the 2's complement number in the AL register half to word length in AX. The cwd (convert word to double) instruction extends the word in AX to a doubleword in DX and AX. The cdq (convert double to quadword) instruction extends the word in EAX to a quadword in EDX and EAX. The cwde (convert word to double extended) instruction extends the word in AX to a doubleword in EAX; this is not an instruction that would normally be used to prepare for division. Each instruction copies the sign bit of the original number to each bit of the high order half of the result. None of these instructions affect flags. Some examples are

Two "move" instructions are somewhat similar to the above "convert" instructions. These instructions copy an 8-bit or 16-bit source operand to a 16-bit or 32-bit destination, extending the source value. The movzx instruction always extends the source value with zero bits. It has the format
movzx register, source
The movsx instruction extends the source value with copies of the sign bit. It has a similar format
movsx register, source
Data about these instructions is in Fig. 4.19. With either instruction the source operand can be in a register or in memory. Neither instruction changes any flag value.
|
Clock Cycles |
Opcode |
||||||
|---|---|---|---|---|---|---|---|
|
Destination |
Source |
386 |
486 |
Pentium |
Number of Bytes |
movsx |
movzx |
|
register 16 |
register 8 |
3 |
3 |
3 |
3 |
0F BE |
0F B6 |
|
register 32 |
register 8 |
3 |
3 |
3 |
3 |
0F BE |
0F B6 |
|
register 32 |
register 16 |
3 |
3 |
3 |
3 |
0F BF |
0F B7 |
|
register 16 |
memory byte |
6 |
3 |
3 |
3+ |
0F BE |
0F B6 |
|
register 32 |
memory byte |
6 |
3 |
3 |
3+ |
0F BE |
0F B6 |
|
register 32 |
memory word |
6 |
3 |
3 |
3+ |
0F BF |
0F B7 |
Figure 4.19: movsx and movzx instructions
Here are a few examples showing how these instructions work.
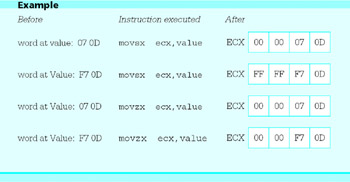
This section concludes with another simple program, this one to convert Celsius (centigrade) temperatures to Fahrenheit. Figure 4.20 gives the source code. The formula implemented is
; program to convert Celsius temperature to Fahrenheit ; uses formula F = (9/5)*C + 32 ; author: R. Detmer ; date: revised 9/97 .386 .MODEL FLAT ExitProcess PROTO NEAR32 stdcall, dwExitCode:DWORD INCLUDE io.h cr EQU 0dh ; carriage return character Lf EQU 0ah ; linefeed character .STACK 4096 ; reserve 4096-byte stack .DATA ; reserve storage for data Prompt1 BYTE CR,LF,"This program will convert a Celsius " BYTE "temperature to the Fahrenheit scale",cr,Lf,Lf BYTE "Enter Celsius temperature: ",0 Value BYTE 10 DUP (?) Answer BYTE CR,LF,"The temperature is" Temperature BYTE 6 DUP (?) BYTE " Fahrenheit",cr,Lf,0 .CODE ; start of main program code _start: Prompt: output Prompt1 ; prompt for Celsius temperature input Value,10 ; read ASCII characters atoi Value ; convert to integer imul ax,9 ; C*9 add ax,2 ; rounding factor for division mov bx,5 ; divisor cwd ; prepare for division idiv bx ; C*9/5 add ax,32 ; C*9/5 + 32 itoa Temperature,ax ; convert to ASCII characters output Answer ; output label and result INVOKE ExitProcess, 0 ; exit with return code 0 PUBLIC _start ; make entry point public END
Figure 4.20: Convert Celsius temperature to Fahrenheit
F = (9/5)* C + 32
where F is the Fahrenheit temperature and C is the Celsius temperature. Since the arithmetic instructions covered so far perform only integer arithmetic, the program gives the integer to which the fractional answer would round. It is important to multiply 9 and C before dividing by 5; the integer quotient 9/5 would be simply 1. Dividing C by 5 before multiplying by 9 produces larger errors than if the multiplication is done first. Why? To get a rounded answer, half the divisor is added to the dividend before dividing. Since the divisor in this formula is 5, the number 2 is added for rounding. Notice that the cwd instruction is used to extend the partial result before division.
Exercises 4.4
- For each part of this problem, assume the "before" values when the given instruction is executed. Give the requested "after" values. Some of these instructions will cause division errors; identify such instructions.
Before
Instruction
After
(a)
EDX: 00 00 00 00
EAX: 00 00 00 9A
EBX: 00 00 00 0Fidiv ebx
EDX, EAX
(b)
AX: FF 75
byte at Count: FCidiv Count
AX
(c)
AX: FF 75
byte at Count: FCdiv Count
AX
(d)
DX: FF FF
AX: FF 9A
CX: 00 00idiv cx
DX, AX
(e)
DX: FF FF FF FF
AX: FF FF FF 9A
CX: FF FF FF C7idiv ecx
EDX, EAX
(f)
DX: 00 00
AX: 05 9A
CX: FF C7idiv cx
DX, AX
(g)
DX: 00 00
AX: 05 9A
CX: 00 00idiv cx
DX, AX
(h)
EDX: 00 00 00 00
EAX: 00 00 01 5D
EBX: 00 00 00 08idiv ebx
EDX, EAX
- Give the opcode for each instruction in Exercise 1.
- This section mentioned two methods of zeroing EDX prior to unsigned division, using
mov edx,0
or
sub edx,edx
Which instruction would give more compact code? Which instruction would execute in fewer clock cycles on a Pentium?
- The Celsius to Fahrenheit temperature conversion program (Fig. 4.20) works for Celsius temperatures that have fairly large magnitude and are either positive or negative. Suppose that you limit the Celsius temperature to the range 0-100 degrees, yielding Fahrenheit temperatures from 32-212. How can the program be modified to take advantage of these limited numeric ranges?
Programming Exercises 4.4
- The formula for converting a Fahrenheit to a Celsius temperature is
C = (5/9) * (F -32)
Write a complete 80×86 assembly language program to prompt for a Fahrenheit temperature and display the corresponding Celsius temperature.
- Write a complete 80×86 assembly language program to prompt for four grades and then display the sum and the average (sum/4) of the grades.
- Write a complete 80×86 assembly language program to prompt for four grades. Suppose that the last grade is a final exam grade that counts twice as much as the other three. Display the sum (adding the last grade twice) and the average (sum/5).
- Write a complete 80×86 assembly language program to prompt for four pairs of grades and weighting factors. Each weighting factor indicates how many times the corresponding grade is to be counted in the sum. The weighted sum is
WeightedSum = Grade1 * Weight1 + Grade2 * Weight2 + Grade3 * Weight3 + Grade4 * Weight4
and the sum of the weights is
SumOfWeights = Weight1 + Weight2 + Weight3 + Weight4
Display the weighted sum, the sum of the weights, and the weighted average (WeightedSum/SumOfWeights).
A sample run might look like
grade 1? 88 weight 1? 1 grade 2? 77 weight 2? 2 grade 3? 94 weight 3? 1 grade 4? 85 weight 4? 3 weighted sum: 591 sum of weights: 7 weighted average: 84
- Write a complete 80×86 assembly language program to prompt for four grades, and then display the sum and the average (sum/4) of the grades in ddd.dd format (exactly three digits before and two digits after a decimal point).
- Write a short program that causes a division by zero to discover how the interrupt handler in your 80×86 system responds.
Addition and Subtraction of Larger Numbers
The add and sub instructions covered in Section 4.2 work with byte-length, word-length, or doubleword-length operands. Although the range of values that can be stored in a doubleword is large, −2,147,483,648 (8000000016) to 2,147,483,647 (7FFFFFFF16), it is sometimes necessary to do arithmetic with even larger numbers. Very large numbers can be added or subtracted a group of bits at a time.
We will illustrate the technique for adding large numbers by adding two 64-bit long numbers. The idea is to start with the low-order 32 bits from each number and add them using an ordinary add instruction. This operation sets the carry flag CF to 1 if there is a carry out of the high order bit and to 0 otherwise. Now the next 32 bits are added using a special addition instruction adc (add with carry). The two high-order 32-bit numbers are added as usual, but if CF is set to 1 from the prior addition, then 1 is added to their sum before it is sent to the destination location. The adc instruction also sets CF, so this process could be continued for as additional groups of bits.
Assume that the two numbers to be added are in four doublewords in the data segment.
Nbr1Hi DWORD ? ; High order 32 bits of Nbr1 Nbr1Lo DWORD ? ; Low order 32 bits of Nbr1 Nbr2Hi DWORD ? ; High order 32 bits of Nbr2 Nbr2Lo DWORD ? ; Low order 32 bits of Nbr2
The following code fragment adds Nbr2 to Nbr1, storing the sum at the doublewords reserved for Nbr1.
mov eax, Nbr1Lo ; Low order 32 bits of Nbr1 add eax, Nbr2Lo ; add Low order 32 bits of Nbr2 mov Nbr1Lo, eax ; sum to destination mov eax, Nbr1Hi ; High order 32 bits of Nbr1 adc eax, Nbr2Hi ; add High order 32 bits of Nbr2 & carry mov Nbr1Hi, eax ; sum to destination
One thing making this code work is that the mov instructions that come between the add and adc instructions do not alter the carry flag. If an intervening instruction did change CF, then the sum could be incorrect.
The adc instructions are identical to corresponding add instructions except that the extra 1 is added if CF is set to 1. For subtraction, sbb (subtract with borrow) instructions function like sub instructions except that if CF is set to 1, an extra 1 is subtracted from the difference. Large numbers can be subtracted in groups of bits, working right to left. Figure 4.21 lists the allowable operand types for adc and sbb instructions. This table is identical to Fig. 4.5 except for a few opcodes.
|
Clock Cycles |
Opcode |
||||||
|---|---|---|---|---|---|---|---|
|
Destination Operand |
Source Operand |
386 |
486 |
Pentium |
Number of Bytes |
adc |
sbb |
|
register 8 |
immediate 8 |
2 |
1 |
1 |
3 |
80 |
80 |
|
register 16 |
immediate 8 |
2 |
1 |
1 |
3 |
83 |
83 |
|
register 32 |
immediate 8 |
2 |
1 |
1 |
3 |
83 |
83 |
|
register 16 |
immediate 16 |
2 |
1 |
1 |
4 |
81 |
81 |
|
register 32 |
immediate 32 |
2 |
1 |
1 |
6 |
81 |
81 |
|
AL |
immediate 8 |
2 |
1 |
1 |
2 |
14 |
1C |
|
AX |
immediate 16 |
2 |
1 |
1 |
3 |
15 |
1D |
|
EAX |
immediate 32 |
2 |
1 |
1 |
5 |
15 |
1D |
|
memory byte |
immediate 8 |
7 |
3 |
3 |
3+ |
80 |
80 |
|
memory word |
immediate 8 |
7 |
3 |
3 |
3+ |
83 |
83 |
|
memory doubleword |
immediate 8 |
7 |
3 |
3 |
3+ |
83 |
83 |
|
memory word |
immediate 16 |
7 |
3 |
3 |
4+ |
81 |
81 |
|
memory doubleword |
immediate 32 |
7 |
3 |
3 |
6+ |
81 |
81 |
|
register 8 |
register 8 |
2 |
1 |
1 |
2 |
12 |
1A |
|
register 16 |
register 16 |
2 |
1 |
1 |
2 |
13 |
1B |
|
register 32 |
register 32 |
2 |
1 |
1 |
2 |
13 |
1B |
|
register 8 |
memory byte |
6 |
2 |
2 |
2+ |
12 |
1A |
|
register 16 |
memory word |
6 |
2 |
2 |
2+ |
13 |
1B |
|
register 32 |
memory doubleword |
6 |
2 |
2 |
2+ |
13 |
1B |
|
memory byte |
register 8 |
7 |
3 |
3 |
2+ |
10 |
18 |
|
memory word |
register 16 |
7 |
3 |
3 |
2+ |
11 |
19 |
|
memory doubleword |
register 32 |
7 |
3 |
3 |
2+ |
11 |
19 |
Figure 4.21: adc and sbb instructions
To apply similar techniques to longer numbers, often a loop of identical instructions is used. If CF is known to be 0 before the loop begins, even the first addition can be done using adc. The 80×86 architecture has three instructions that let the programmer manipulate the carry flag. They are summarized in Fig. 4.22. There are no separate columns for the number of clock cycles on different processors since these instructions take two clock cycles on each of 30386, 80486, and Pentium processors.
|
Instruction |
Operation |
Clock Cycles |
Number of Bytes |
Opcode |
|---|---|---|---|---|
|
clc |
clear carry flag (CF := 0) |
2 |
1 |
F8 |
|
stc |
set carry flag |
2 |
1 |
F9 |
|
cmc |
complement carry flag |
2 |
1 |
F5 |
Figure 4.22: Control of carry flag CF
Multiplication and division operations with longer numbers are even more involved than addition and subtraction. Often techniques for adding and subtracting longer numbers are used to implement algorithms that are similar to grade school multiplication and division procedures for decimal numbers.
If one really needs to use longer numbers, it takes more than a set of arithmetic procedures. One may also need procedures like itoa and atoi in order to convert long numbers to and from ASCII character format.
Exercises 4.5
- Suppose that two 96 bit long numbers are to be added.
- Show how storage for three such numbers can be reserved in the data segment of a program.
- Give a fragment of 80×86 code that will add the second number to the first, storing the sum at the locations reserved for the first number.
- Give a fragment of 80×86 code that will add the second number to the first, storing the sum at the locations reserved for the third number.
- Suppose that two 64 bit numbers are stored as shown in the example in this section. Give a fragment of 80×86 code that will subtract Nbr2 from Nbr1, storing the difference at the locations reserved for Nbr1.
- For each part of this problem, assume the "before" values when the given instruction is executed. Give the requested "after" values.
Before
Instruction
After
(a)
EAX: 00 00 03 7D
ECX: 00 00 01 A2
CF: 0adc eax,ecx
EAX, CF
(b)
EAX: 00 00 03 7D
ECX: 00 00 01 A2
CF: 1adc eax,ecx
EAX, CF
(c)
EAX: FF 49 00 00
ECX: 03 68 00 00
CF: 0adc eax,ecx
EAX, CF
(d)
EAX: FF 4900 00
ECX: 03 6800 00
CF: 1adc eax,ecx
EAX, CF
(e)
EAX: 00 00 03 7D
ECX: 00 00 01 A2
CF: 0sbb eax,ecx
EAX, CF
(f)
EAX: 00 00 01 A2
ECX: 00 00 03 7D
CF: 1sbb eax,ecx
EAX, CF
Something Extra Levels of Abstraction and Microcode
In computer science, we look at computers and computation at many levels. When using an application program like a word processing package or a game, we just want its various features to work and we typically do not care how it is written. When we are writing programs in a high-level language, we tend to view the computer as say, an Ada machine or a C++ machine, and often do not think about how various language constructs are implemented. The application level and the high-level language level are two levels of abstraction. As used here, the word "abstraction" can be thought of as "ignoring the details."
This book deals primarily with the machine-language level of abstraction. One of the book's primary objectives is to relate this level to the high-level language level of abstraction. To a hardware designer, it is even more important to relate the machine-language level to lower levels of abstraction.
What lower levels are there? Obviously the hardware of the computer somehow has to execute an instruction like add or imul. The hardware level of a machine is often viewed as a collection of logic circuits, although you can take an even lower view of these as constructed with transistors, etc. For relatively simple architectures, electronic circuits can be designed to implement each possible instruction directly.
For more complex instruction sets, there is usually another level of abstraction between the machine language that the user sees and the digital circuitry of the machine. This microcode level consists of a collection of routines that actually implement the instructions. The microinstructions are normally stored in permanent memory in the CPU itself. A CPU that uses microcode has a collection of internal scratchpad registers that are not directly accessible to the user and simple circuitry such as an adder. A machine language instruction is implemented by a series of microinstructions that do have access to these scratchpad registers. Microcode resembles machine language. However, there are many differences. Microinstructions typically have bits that directly control circuits. Often there is no program counter-each instruction contains the address of the next instruction. In general, microprogramming is more complex than assembly language programming.
Summary
The Intel 80×86 mov instruction is used to copy data from one location to another. All but a few combinations of source and destination locations are allowed. The xchg instruction swaps the data stored at two locations.
The 80×86 architecture has a full set of instructions for arithmetic with byte-length, word-length, and doubleword-length integers. The add and sub instructions perform addition and subtraction; inc and dec add and subtract 1, respectively. The neg instruction negates its operand.
There are two multiplication and two division mnemonics. The imul and idiv instructions assume that their operands are signed 2's complement numbers; mul and div assume that their operands are unsigned. Many multiplication instructions start with single-length operands and produce double-length products; other formats form a product the same length as the factors. Division instructions always start with a double-length dividend and single-length divisor; the outcome is a single-length quotient and a single-length remainder. The cbw, cwd, and cdq instructions aid in producing a double-length dividend before signed division. Flag settings indicate possible errors during multiplication; an error during division produces a hardware exception that invokes a procedure to handle the error.
Instructions that have operands in registers are generally faster than those that reference memory locations. Multiplication and division instructions are slower than addition and subtraction instructions.
The adc and sbb instructions make it possible to add numbers longer than doublewords a group of bits at a time, incorporating a carry or borrow from one group into the addition or subtraction of the next group to the left. The carry or borrow is recorded in the carry flag CF. The 80×86 clc, stc, and cmc instructions enable the programmer to clear, set, and complement the carry flag when necessary.
The machine language level is just one level of abstraction at which a computer can be viewed. Above this level are the high-level language level and the application level. Below the machine language level are the microcode level and the hardware level.
Preface
- Representing Data in a Computer
- Parts of a Computer System
- Elements of Assembly Language
- Basic Instructions
- Branching and Looping
- Procedures
- String Operations
- Bit Manipulation
- The Assembly Process
- Floating-Point Arithmetic
- Decimal Arithmetic
- Input/Output
- Appendix A Hexadecimal/ASCII conversion
- Appendix B Useful MS-DOS Commands
- Appendix C MASM 6.11 Reserved Words
- Appendix D 80x86 Instructions (by Mnemonic)
- Appendix E 80x86 Instructions (by Opcode)
EAN: 2147483647
Pages: 113
