8.6 Conditional Logic

^def is a rather weak language. For example, although it can express the fact that a certain default holds, it cannot express the fact that a certain default does not hold, since ^def does not allow negated defaults. There is no great difficulty extending the language to allow negated and nested defaults, and many agents as well. Let be the language defined by starting with primitive propositions, and closing off under ∧, , and →_i, i = 1, …, n. A formula such as φ →_i ψ should be read as "according to agent i, φ's are typically ψ's." Formulas in can describe logical combination of defaults (e.g., (p →₁ q) ∨ (p →₁ q)), negated defaults (e.g., (p →₁ q)), and nested defaults (e.g., (p →₁ q) →₂ r).

There is no difficulty giving semantics to formulas in in and (where are the obvious generalizations of ^ps and ^qual to n agents), just by extending the definition in the single-agent case in the obvious way. For example, if then

where Note that, since the possibility measure may depend on the world and the agent, the world w must now explicitly appear on the left-hand side of ⊨ and → must have subscripts denoting agents.

^→ with this semantics has been called conditional logic. Statements of the form φ → ψ are called conditionals (but not material conditionals, of course!).

It should be clear from the definitions that formulas in can be expressed in

Proposition 8.6.1

For every structure M in ^poss_n, ^pref_n, ^rank_n and ^qual_n,

Proof The result is immediate from the definitions.

What about the converse? Can all formulas in ^RL_n be expressed in ^→_n? In ^poss_n, ^rank_n, and ^pref_n they can.

Proposition 8.6.2

For every structure M in ^poss_n, ^rank_n, and ^pref_n,

Proof See Exercise 8.43.

The key step in the proof of Proposition 8.6.2 involves showing that M ⊨ ℓ_i(φ) > ℓ_i(ψ) iff M ⊨ ℓ_i(φ ∧ ψ) > ℓ_i(ψ). While this property holds for structures M in ^poss_n, ^rank_n, and ^pref_n, it does not hold in ^qual_n in general, so Proposition 8.6.2 does not extend to ^qual_n In fact, there is no formula in ^→_n that is equivalent to ℓ_i(φ) > ℓ_i(ψ) in all structures in ^qual_n (Exercise 8.44). Thus, in ^qual_n, the language ^RL_n is strictly more expressive than ^→_n

Although it is possible to translate ^→_n to ^RL_n and then use AX^ord_n (in the case of plausibility measures and partial preorders) or AX^RLTe (in the case of possibility measures and ranking functions, since they define total preorders) to reason about defaults, it is desirable to be able to characterize default reasoning directly in the language ^→_n. Of course, the characterization will depend to some extent on whether the underlying order is partial or total.

Let AX^cond consist of the following axioms and inference rules:

Prop. All substitution instances of propositional tautologies.

C1. φ →_i φ.
C2. ((φ →_i ψ₁) ∧ (φ →_i ψ₂)) ⇔ (φ →_i (ψ₁ ∧ ψ₂)).
C3. ((φ₁ →_i ψ) ∧ (φ₂ →_i ψ)) ⇔ ((φ₁ ∨ φ₂) →_i ψ).
C4. ((φ →_i ψ₁) ∧ (φ →_i ψ₂)) ⇔ ((φ ∧ ψ₂) →_i ψ₁).
MP. From φ and φ ⇔ ψ infer ψ.
RC1. From φ ⇔ φ′ infer (φ →_i ψ) ⇔ (φ′ →_i ψ).
RC2. From ψ ⇔ ψ′ infer (φ →_i ψ) ⇔ (φ →_i ψ′).

AX^cond can be viewed as a generalization of P. For example, the richer language allows the AND to be replaced with the axiom C2. Similarly, C1, C3, C4, RC1, and RC2 are the analogues of REF, OR, CM, LLE, and RW, respectively. As usual, Prop and MP are needed to deal with propositional reasoning.

Theorem 8.6.3

AX^cond_n is a sound and complete axiomatization for the language ^→_n with respect to both ^pref_n and ^qual_n.

Proof As usual, soundness is straightforward (Exercise 8.45) and completeness is beyond the scope of this book.

The language ^def cannot distinguish between notions of likelihood based on partial preorders and ones based on total preorders. Conditional logic can make this distinction and others as well. Consider the following two axioms:

C5. (φ →_i ψ₁) ∧ (φ →_i ψ₂) ⇔ ((φ ∧ ψ₂) →_i ψ₁).
C6. (true →_i false).
C5 is almost the same as C4, except that the clause φ →_i ψ₂ in C4 is replaced by (φ →_i ψ₂) in C5. C5 expresses a property called Rational Monotonicity in the literature. Roughly speaking, it is what distinguishes notions of uncertainty where the underlying notion of likelihood puts a total preorder on events from ones where the preorder is only partial. C5 does not hold in general in 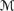^qual_n or 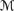^pref_n (Exercise 8.46), but it does hold in 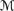^poss_n, 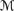^rank_n, and 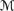^tot_n. Reverse engineering shows that C5 corresponds to the following property of plausibility measures:
Pl6. If Pl(U ∩ U′) > Pl(U ∩ U′) and Pl(V ∩ U′) ≯ Pl(V ∩ U′), then Pl(U ∩ V ∩ U′) > Pl(U ∩ V ∩ U′).

Just as Pl4′ is equivalent to the arguably more natural Pl4 (in the presence of Pl3), so too Pl6 is equivalent to arguably more natural properties in the presence of Pl3 and Pl4. The first is a property that is closely related to the assumption that disjoint sets are totally ordered; the second is closely related to the union property (see Exercises 8.47 and 8.48 for more details on these relationships).
Pl7. If U₁, U₂, and U₃ are pairwise disjoint and Pl(U₁) < Pl(U₂), then either Pl(U₃) < Pl(U₂) or Pl(U₁) < Pl(U₃) (or both).
Pl8. If U₁, U₂, and U₃ are pairwise disjoint and Pl(U₁) < Pl(U₂ ∪ U₃), then either Pl(U₁) < Pl(U₂) or Pl(U₁) < Pl(U₃) (or both).

Proposition 8.6.4

In the presence of Pl3 and Pl4, Pl7 and Pl8 together are equivalent to Pl6.

Proof See Exercise 8.49.

Since Pl7 and Pl8 clearly hold in ^poss_n, ^rank_n, and ^tot_n (indeed, they hold without the restriction to disjoint sets), this explains why they all satisfy C5.

C6 corresponds to a property called normality in the literature. It holds for a plausibility measure Pl if it satisfies the following property:
Pl9. Pl(W) > ⊥.

This property holds for the plausibility measures arising from ranking functions, possibility measures, and probability sequences.

Call a plausibility measure rational if it satisfies Pl6 (or, equivalently, Pl7 and Pl8) and normal if it satisfies Pl9. Ranking functions and possibility measures are both rational and normal; PS structures also give rise to normal (but not necessarily rational) plausibility measures. The following theorem shows that C5 characterizes qualitative rational structures and C6 characterizes qualitative normal structures. Moreover, these axioms suffice to characterize reasoning about ^→ in ^ps_n, ^poss_n, ^rank_n, and ^tot_n. Let ^rat_n (resp., ^norm_n; ^rat,norm_n) consist of all qualitative plausibility structures for n agents whose plausibility measure satisfies Pl7 and Pl8 (resp., Pl9; Pl7–9).

Theorem 8.6.5

AX^cond_n + {C5} is a sound and complete axiomatization for the language 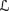^→_n with respect to 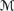^rat_n.
AX^cond_n + {C6} is a sound and complete axiomatization for the language 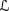^→_n with respect to 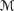^norm_n and 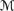^ps_n.
AX^cond_n +{C5, C6} is a sound and complete axiomatization for the language 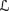^→n with respect to 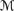^rat,norm_n, ^tot_n, ^rank_n, and ^poss_n.