8.5 Beyond System P

8.5 Beyond System P

As I said before, the axiom system P has been viewed as characterizing the "conservative core" of default reasoning. Is there a reasonable, principled way of going beyond System P to obtain inferences that do not follow from treating → as material implication? The kinds of inference of most interest involve ignoring "irrelevant" information and allowing subclasses to inherit properties from superclasses. The following examples give a sense of the issues involved:

Example 8.5.1

If birds typically fly and penguins typically do not fly (although penguins are birds), it seems reasonable to conclude that red penguins do not fly. Thus, if Σ₁ is as in Example 8.3.1, then it might seem reasonable to expect that penguin ∧ red → fly follows from Σ₁. However, Σ₁ ⊬_P penguin ∧ red → fly (Exercise 8.37(a)). Intuitively, this is because it is conceivable that although penguins typically do not fly, red penguins might be unusual penguins, and so might in fact fly. Much as we might like to treat redness as irrelevant, it might in fact be relevant to whether or not penguins fly. The "conservative core" does not let us conclude that red penguins do not fly because of this possibility.

Notice that Σ₁ says only that penguins are typically birds, rather than all penguins are birds. This is because universal statements cannot be expressed in ^def. The point here could be made equally well if penguin → bird were replaced by penguin ⇔ bird in Σ₁. There is no problem handling a mix of properties involving both the material conditional and the default conditional. (However, as Example 8.3.1 shows, replacing all occurrences of → by ⇔ has significant consequences.)

Now suppose that the default "birds typically have wings" is added to Σ₁. Let

Does it follow from Σ₂ that penguins typically have wings? This property has been called exceptional subclass inheritance in the literature: although penguins are an exceptional subclass of birds (in that they do not fly, although birds typically do), it seems reasonable for them to still inherit the property of having wings from birds. This property holds for the material conditional, since material implication is transitive. (That is, penguin ⇔ winged follows from penguin ⇔ bird and bird ⇔ winged.) However, it does not hold for → in general. For example, Σ₂ ⊬_P penguin → winged (Exercise 8.37(b)). After all, if penguins are atypical birds in one respect, they may also be atypical in other respects.

But suppose that Σ₃ = Σ₁ ∪{yellow → easy-to-see}: yellow things are easy to see. It certainly seems reasonable to expect that yellow penguins are typically easy to see.

However, Σ₃ ⊬_P (penguin ∧ yellow) → easy-to-see (Exercise 8.37(c)). Note that this type of exceptional subclass inheritance is somewhat different from that exemplified by Σ₂. Whereas penguins are atypical birds, there is no reason to expect them to be atypical yellow objects. Nevertheless, it does not follow from P that yellow penguins inherit the property of being easy to see.

One last example: Suppose that Σ₄ = Σ₂ ∪{robin → bird}. Does it follow from Σ₄ that robins typically have wings? Although penguins are atypical birds, as far as Σ₄ is concerned, robins are completely unexceptional birds, and birds typically have wings. Unfortunately, it is not hard to show that Σ₄ ⊬_P robin → winged, nor does it help to replace robin by robin ∧ bird (Exercise 8.37(d)).

In light of these examples, it is perhaps not surprising that there has been a great deal of effort devoted to finding principled methods of going beyond P. However, it has been difficult to find one that gives all and only the "reasonable" inferences, whatever they might be. The results of the previous section point to one source of the difficulties. We might hope to find (1) an axiom system P⁺ that is stronger than P (in the sense that everything provable in P is also provable in P⁺, and P⁺ can make some additional "reasonable" inferences) and (2) a class of structures with respect to which P⁺ is sound and complete. If the structures in can be viewed as plausibility structures, then they must all satisfy Pl4 and Pl5 to guarantee that P is sound with respect to . However, cannot be rich, for then P would also be complete; no additional inferences could be drawn.

Richness is not a very strong assumption and it is not easy to avoid. One way of doing so that has been taken in the literature is the following: Given a class of structures, recall that Σ ⊨ φ if M ⊨ Σ implies M ⊨ φ for every structure M ∈ . Rather than considering every structure that satisfies Σ, the idea is to consider a "preferred" structure that satisfies Σ and to check whether φ holds in that preferred structure. Essentially, this approach takes the idea used in preferential structures of considering the most preferred worlds and lifts it to the level of structures. This gets around richness since only one structure is being considered rather than a whole collection of structures. It is clear that one structure by itself cannot in general hope to satisfy the richness condition.

Here are two examples of how this general approach works. The first uses ranking structures (which are, after all, just a special case of plausibility structures). Suppose that an agent wants to reason about some phenomena involving, say, birds, described by some fixed set Φ of primitive propositions. Let W_Φ consist of all the truth assignments to the primitive propositions in Φ. Let consist of all simple ranking structures of the form (W_Φ, κ, π_Φ), where π_Φ(w) = w (this makes sense since the worlds in W_Φ are truth assignments). Define a partial order ≽ on ranking functions on W_Φ by defining κ₁ ≽ κ₂ if κ₁(w) ≤ κ₂(w) for all w ∈ W_Φ. Thus, κ₁ is preferred to κ₂ if every world is no more surprising according to κ₁ than it is according to κ₂. The order ≽ can be lifted to a partial order on ranking structures in by defining (W_Φ, κ₁, π_Φ) ≽ (W_Φ, κ₂, π_Φ) if κ₁ ≽ κ₂.

Given a finite set Σ of formulas in ^def (Φ), let consist of all the ranking structures in that satisfy all the defaults in Σ. Although ≽ is a partial order on ranking structures, it turns out that if ≠ ⊘, then there is a unique structure M_Σ ∈ that is most preferred. That is, M_Σ ≽ M for all M ∈ (Exercise 8.38). Intuitively, M_Σ makes worlds as unsurprising as possible, while still satisfying the defaults in Σ. For φ ∈ ^def, define if either = ⊘ or M_Σ ⊨ φ. That is, if φ is true in the most preferred structure of all the structures satisfying Σ. (The superscript Z is there because this approach has been called System Z in the literature.)

Since P is sound in ranking structures, it certainly follows that if Σ ⊢_P φ. But the System Z approach has some additional desirable properties. For example, as desired, red penguins continue not to fly, that is, in the notation of Example 8.5.1, penguin ∧ red → fly. More generally, System Z can ignore "irrelevant" attributes and deals well with some of the other issues raised by Example 8.5.1, as the following lemma shows:

Lemma 8.5.2

Let Σ_a ={φ₁ → φ₂, φ₂ → φ₃} and let Σ_b = Σ_a ∪{φ₁ → φ₃, φ₁ → φ₄}.

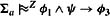1. if φ₁ ∧ φ₂ ∧ φ₃ ∧ ψ is satisfiable.

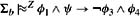2. if φ₃ ∧ φ₄ if φ₁ ∧ φ₂ ∧ φ₃ ∧ φ₄ ∧ ψ is satisfiable.

Proof For part (a), suppose that φ₁ ∧ φ₂ ∧ φ₃ ∧ ψ is satisfiable. Then , since both defaults in Σ_a are satisfied in a structure where all worlds in which φ₁ ∧ φ₂ ∧ φ₃ is true have rank 0 and all others have rank 1. Suppose that M_Σa = (W, κ₁, π). In M_Σa, it is easy to see that all worlds satisfying φ₁ ∧ φ₂ ∧ φ₃ have rank 0 and all worlds satisfying φ₁ ∧ φ₂ or φ₂ ∧ φ₃ have rank 1 (Exercise 8.39(a)). Since, by assumption, φ₁ ∧ φ₂ ∧ φ₃ ∧ ψ is satisfiable, there is a world of rank 0 satisfying this formula. Moreover, since any world satisfying φ₁ ∧ φ₃ ∧ ψ must satisfy either φ₁ ∧ φ₂ or φ₂ ∧ φ₃, it follows that κ₁(〚φ₁ ∧ φ₃ ∧ ψ〛_MΣa) ≤ 1. Thus, κ₁(〚φ₁ ∧ φ₃ ∧ ψ〛_MΣa) < κ₁(〚φ₁ ∧ φ₃ ∧ ψ〛_MΣa), so M_Σa ⊨ φ₁ ∧ ψ → φ₃.

For part (b), if then the result is trivially true. Otherwise, suppose that M_Σb = (W, κ₂, π). It can be shown that (i) all worlds in M_Σb satisfying φ₁ ∧ φ₂ ∧ φ₃ have rank 0, (ii) there are some worlds in M_Σb satisfying φ₁ ∧ φ₂ ∧ φ₃, (iii) all worlds satisfying φ₁ ∧ φ₂ ∧ φ₃ ∧ φ₄ have rank 1, and (iv) all worlds satisfying φ₁ ∧ φ₃ or φ₁ ∧ φ₄ have rank 2 (Exercise 8.39(b)). Since, by assumption, φ₁ ∧ φ₂ ∧ φ₃ ∧ φ₄ ∧ ψ is satisfiable, there is a world of rank 1 satisfying this formula. It follows that κ₂(〚φ₁ ∧ ψ ∧ φ₃ ∧ φ₄〛_MΣb) < κ₂(〚φ₁ ∧ ψ ∧ (φ₃ ∨ φ₄)〛_MΣb), so M_Σb ⊨ φ₁ ∧ ψ → φ₃ ∧ φ₄.

Part (a) says that in the System Z approach, red robins do fly (taking φ₁ = robin, φ₂ = bird, φ₃ = fly, and ψ = red). Part (b) says that if penguins have wings, then red penguins have wings but do not fly (taking φ₁ = penguin, φ₂ = bird, φ₃ = fly, φ₄ = winged, and ψ = red). Indeed, it follows from Σ_b (with this interpretation of the formulas) that red penguins have all the properties that penguins have. But red penguins do not necessarily inherit properties of birds, such as flying. So, for these examples, System Z does the "right" things. However, System Z does not always deliver the desired results. In particular, not only do penguins not inherit properties of birds such as flying (which, intuitively, they should not inherit), they also do not inherit properties of birds like having wings (which, intuitively, there is no reason for them not to inherit). For example, returning to Example 8.5.1, notice that it is neither the case that (penguin ∧ bird) → winged nor that (penguin ∧ yellow) → easy-to-see (Exercise 8.40). The next approach I consider has these properties.

This approach uses PS structures. Given a collection Σ of defaults, let Σ^k consist of the statements that result by replacing each default φ → ψ in Σ by the ^QU formula ℓ(ψ|φ)≥ 1 − 1/k. Let ^k be the set of probability measures that satisfy these formulas. More precisely, let If ^k ≠ ⊘, let be the probability measure of maximum entropy in ^k. (It can be shown that there is a unique probability measure of maximum entropy in this set, since it is defined by linear inequalities, but that is beyond the scope of this book.) As long as ^k ≠ ⊘ for all k ≥ 1, this procedure gives a probability sequence Let Define the relation as follows: if either there is some k such that ^k ≠ ⊘ (in which case ^k′ ≠ ⊘ for all k′ ≥ k) or

P is again sound for the maximum-entropy approach.

Proposition 8.5.3

If Σ ⊢_P φ then

Proof Suppose that Σ ⊢ φ. It is easy to show that if ^k = ⊘ for some k > 0, then there is no structure M ∈ ^ps such that M ⊨ Σ. On the other hand, if ^k ≠ ⊘ for all k ≥ 1, then (Exercise 8.41). The result now follows immediately from Theorem 8.4.4.

Standard properties of maximum entropy can be used to show that has a number of additional attractive properties. In particular, it is able to ignore irrelevant attributes and it sanctions inheritance across exceptional subclasses, giving the desired result in all the cases considered in Example 8.5.1.

Lemma 8.5.4

Let Σ_a ={φ₁ → φ₂, φ₂ → φ₃}, Σ_b = Σ_a ∪{φ₁ → φ₃, φ₁ → φ₄}, Σ_c = Σ_a ∪{φ₁ → φ₃, φ₂ → φ₄}, and Σ_d = Σ_a ∪{φ₁ → φ₃, φ₅ → φ₄}.

1. Σ_a 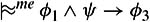if φ₁ ∧ φ₂ ∧ φ₃ ∧ ψ is satisfiable.

2. Σ_b 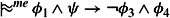if φ₁ ∧ φ₂ ∧ φ₃ ∧ φ₄ ∧ ψ is satisfiable.

3. Σ_c 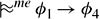if φ₁ ∧ φ₂ ∧ φ₃ ∧ φ₄ is satisfiable.

4. Σ_d 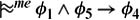if φ₁ ∧ φ₂ ∧ φ₃ ∧ φ₄ ∧ φ₅ is satisfiable.

Notice that parts (a) and (b) are just like Lemma 8.5.2. Part (c) actually follows from part (d). (Taking φ₅ = φ₂ in part (d) shows that if φ₁ ∧ φ₂ ∧ φ₃ ∧ φ₄ is satisfiable. Part (c) then follows using the CUT rule; see Exercise 8.42.) In terms of the examples we have been considering, part (b) says that penguins inherit properties of birds; in particular, they have wings. Part (d) says that yellow penguins are easy to see.

While the proof of Lemma 8.5.4 is beyond the scope of this book, I can explain the basic intuition. It depends on the fact that maximum entropy makes things "as independent as possible." For example, given a set of constraints of the form ℓ(ψ | φ) = α and a primitive proposition q that does not appear in any of these constraints, the structure that maximizes entropy subject to these constraints also satisfies ℓ(ψ | φ ∧ q) = α. Now consider the set Σ₂ of defaults from Example 8.5.1. Interpreting these defaults as constraints, it follows that μ^me_n (winged | bird) ≅ 1 − 1/n (most birds fly) and μ^me_n (bird | penguin) ≅ 1 − 1/n (most birds are penguins). By the previous observation, it also follows that μ^me_n (winged | bird ∧ penguin) ≅ 1 − 1/n. Thus,

(In the last step, I am ignoring the 1/n² term, since it is negligible compared to 1/2n for n large.) Thus, penguin → winged, as desired.

The maximum-entropy approach may seem somewhat ad hoc. While it seems to have a number of attractive properties, why is it the appropriate thing to use for non-monotonic reasoning? One defense of it runs in the spirit of the usual defense of maximum entropy. If Σ_n is viewed as a set of constraints, the probability measure μ^me_n is the one that satisfies the constraints and gives the least "additional information" over and above this fact. But then why consider a sequence of measures like this at all? Some further motivation for the use of such a sequence will be given in Chapter 11. There is also the problem of characterizing the properties of this maximum-entropy approach, something that has yet to be done. Besides the attractive properties described in Lemma 8.5.4, the approach may have some not-so-attractive properties, just as maximum entropy itself has unattractive properties in some contexts. Without a characterization, it is hard to feel completely comfortable using this approach.