8.4 Semantics for Defaults

There have been many attempts to give semantics to formulas in ^def. The surprising thing is how many of them have ended up being characterized by the axiom system P. In this section, I describe a number of these attempts. I conclude with a semantics based on plausibility measures that helps explain why P characterizes so many different approaches. It turns out that Pl4 is the key property for explaining why P is sound.

8.4.1 Probabilistic Semantics

One compelling approach to giving semantics to defaults is based on the intuition that φ → ψ should mean that when φ is the case, ψ is very likely. Suppose that uncertainty is represented using a probability measure μ. In that case, "when φ is the case, ψ is very likely" should mean that the probability of ψ given φ is high, or at least significantly higher than the probability of ψ given φ.

But how high is high enough? Consider a simple measurable probability structure M = (W, μ, π). (In the next two sections I consider only simple structures, which makes it easier to focus on the basic issues of default reasoning.) The first thought might be to emulate the definition of belief and take φ → ψ to hold in M if the conditional probability of ψ given φ is 1. This essentially works, but there is one subtlety that must be dealt with. What happens if the probability of φ is 0? This turns out to be a significant problem in the context of default reasoning. Consider again the set of defaults Σ₁ from Example 8.3.1. Ignoring for a moment the issue of dividing by 0, satisfying this collection of defaults requires that μ(〚fly〛_M | 〚bird〛_M) = 1, μ(〚fly〛_M | 〚penguin〛_M) = 0, and μ(〚bird〛_M | 〚penguin〛_M) = 1. These requirements together imply that μ(〚penguin〛_M) = 0 (Exercise 8.15). Thus, conditioning on sets of measure 0 is unavoidable with this approach. Taking φ → ψ to hold vacuously if μ(〚φ〛) = 0 leads to the same difficulties as interpreting → as ⇔; for example, it then follows that penguin → fly. Some other approach must be found to deal with conditioning on sets of measure 0.

There is a simple solution to this problem: take μ to be a conditional probability measure, so that μ(〚ψ〛_M | 〚φ〛_M) can be defined even if μ(〚φ〛_M) = 0. This, in fact, works. Define a simple measurable conditional probability structure to be one of the form M = (W, 2^W, 2^W − {∅}, μ, π). The fact that ′ = 2^W − {⊘} means that it is possible to condition on all nonempty sets. I abbreviate this as (W, μ, π), just as in the case of a simple measurable structure. It should be clear from context whether μ is a conditional probability measure or an unconditional probability measure. Define M ⊨ φ → ψ if μ(〚ψ〛_M | 〚φ〛_M) = 1. Let ^cps be the class of all simple measurable conditional probability structures.

This definition of defaults in conditional probability structures satisfies all the axioms and rules of axiom system P. In fact, it is characterized by P. (That is, P can be viewed as a sound and complete axiomatization of default reasoning for ^def with respect to such simple conditional probability structures.) If Σ is a finite set of default formulas, write M ⊨ Σ if M ⊨ σ for every formula Σ ∈ Σ. Given a collection of structures, write Σ⊨ φ if, for all M ∈ , if M ⊨ Σ then M ⊨ φ. Thus, Σ⊨ φ holds if every structure in that satisfies the formulas in Σ also satisfies φ. This is a generalization of the definition of validity, since ⊘⊨ φ iff φ is valid in M.

Theorem 8.4.1

If Σ is a finite set of formulas in ^def, then Σ ⊢_P φ → ψ iff Σ⊩_^cps φ → ψ.

Proof I leave it to the reader to check soundness (Exercise 8.16). Soundness also follows from two results proved in Section 8.4.3: Theorem 8.4.10, a more general soundness result, which applies to many classes of structures, and Theorem 8.4.11, which shows that Theorem 8.4.10 applies in particular to ^cps. Completeness follows from two other theorems proved in Section 8.4.3: Theorem 8.4.14, a more general completeness result, which applies to many classes of structures, and Theorem 8.4.15, which shows that Theorem 8.4.14 applies in particular to ^cps.

Although conditional probability measures provide a model for defaults, there may be some conceptual difficulties in thinking of the probability of penguin as being 0. (There is also the question of what event penguin represents. Is μ(〚penguin〛) the probability that a particular bird is a penguin? The probability that a bird chosen at random is a penguin? In the latter case, from what set is the bird being chosen? I ignore these issues for now. They are dealt with in more detail in Chapters 10 and 11.) Perhaps penguins are unlikely, but surely they do not have probability 0. Thus, there has been some interest in getting a probabilistic interpretation of defaults that does not involve 0.

One thought might be to consider a definition somewhat in the spirit of the plausibilistic definition of belief discussed in Section 8.1. Suppose that is a simple measurable probability structure and that φ → ψ is taken to be true in M if μ(〚φ〛_M) = 0 or μ(〚ψ〛_M | 〚φ〛_M) > μ(〚 ψ〛_M | 〚φ〛_M). It is easy to check that, under this interpretation, M ⊨ φ → ψ if and only if μ(〚φ〛_M) = 0 or μ(〚φ ∧ ψ〛_M) > μ(〚φ ∧ ψ〛_M), or, equivalently, if and only if μ(〚φ〛_M) = 0 or μ(〚ψ〛_M | 〚φ〛_M) > 1/2. Moreover, this interpretation satisfies LLE, RW, and REF (Exercise 8.17). However, it does not necessarily satisfy AND, OR, or CM, as the following example shows:

Example 8.4.2

Consider the simple probability structure M₁ from Example 7.3.1. Then

μ(〚 p ∨ q〛_M₁) = μ({w₂, w₃, w₄}) = .75,
μ(〚 p〛_M₁) = μ({w₃, w₄}) = .5,
μ(〚 q〛_M₁) = μ({w₂, w₄}) = .45, and
μ(〚 p ∧ q〛_M₁) = μ({w₄}) = .2.

Thus, μ(〚 p〛_M₁ | 〚 p ∨ q〛_M₁) > .5 and μ(〚 q〛_M₁ | 〚 p ∨ q〛_M₁) > .5, but μ(〚 p ∧ q〛_M₁ | 〚 p ∨ q〛_M₁) < .5. So M₁ ⊨ ( p ∨ q) → p and M₁ ⊨ ( p ∨ q) → q, but violating the AND rule. Moreover, (since 〚( p ∨ q) ∧ p〛_M₁ = 〚 p〛_M₁ and μ(〚 q〛_M₁ | 〚 p〛_M₁) < .5). This is a violation of CM. It is also possible to construct a violation of OR in M₁ (Exercise 8.18).

Perhaps the problem is the choice of 1/2. Another thought might be to define M ⊨ φ → ψ if and only if μ(〚φ〛_M) = 0 or μ(〚ψ〛_M | 〚φ〛_M) > 1 − ∊, for some fixed, small ∊. This interpretation fares no better than the previous one. Again, it is easy to see that it satisfies LLE, RW, and REF, but not AND, CM, or OR (Exercise 8.19).

The problem here is that no fixed ∊ will work. For any fixed ∊, it is easy to construct counterexamples. One solution to this problem is to allow infinitesimals. That is, using the notation of Section 3.2, if μ^ns is a nonstandard probability measure, then φ → ψ holds if the closest standard real number to μ^ns(〚ψ〛 | 〚φ〛) is 1. It is not hard to show that this approach does indeed satisfy all the properties of P (Exercise 8.20), although the conceptual problem of assigning a probability that is essentially 0 to penguins still remains.

As Theorem 8.4.1 shows, using conditional probability measures works as well; there is yet another approach that uses only standard (unconditional) probability measures. It sidesteps the problem of specifying an ∊ by taking, not one, but a sequence of probability measures and requiring that the probability of ψ given φ go to 1 in the limit. With this approach, the probability of penguin is not 0, although it does get arbitrarily close. Since this approach is also related to some of the discussion in Chapter 11, I explore it in a little more detail here.

Definition 8.4.3

A probability sequence on W is just a sequence (μ₁, μ₂, …) of probability measures on W (where, implicitly, every subset of W is measurable with respect to every probability measure in the sequence). A (simple) PS structure is a tuple (W, (μ₁, μ₂, …), π), where (μ₁, μ₂, …) is a probability sequence on W. Let ^ps be the class of all simple PS structures. In a simple PS structure, the truth of a formula of the form φ → ψ is independent of the world. If M = (W, (μ₁, μ₂, …), π) is a simple PS structure, then

where μ_k(〚ψ〛_M | 〚φ〛_M) is taken to be 1 if μ_k(〚φ〛_M) = 0.

This definition is also characterized by P.

Theorem 8.4.4

If Σ is a finite set of formulas in ^def, then Σ ⊢_P φ → ψ iff Σ ⊩_ps φ → ψ.

Proof Again, soundness follows from Theorems 8.4.10 and Theorem 8.4.12. However, it can also be proved directly. For example, consider the AND rule. Suppose that M is a simple PS structure such that M ⊨ φ → ψ₁ and M ⊨ φ → ψ₂. Then lim_k→∞ μ_k(〚ψ₁〛_M | 〚φ〛_M) = 1 and lim_k→∞ μ_k(〚ψ₂〛_M | 〚φ〛_M) = 1. By definition, for all ∊, there must be some k such that μ_k(〚ψ₁〛_M | 〚φ〛_M) ≥ 1 − ∊ and μ_k(〚ψ₂〛_M | 〚φ〛_M) ≥ 1 − ∊. By the inclusion-exclusion rule (2.5),

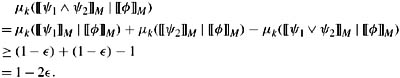
Thus, lim_k→∞ μ_k(〚ψ₁ ∧ ψ₂〛_M | 〚φ〛_M) = 1, so M ⊨ φ → (ψ₁ ∧ ψ₂), as desired. The proof that OR and CM also hold in PS structures is equally straightforward (Exercise 8.21).

Completeness again follows from Theorem 8.4.14 and Theorem 8.4.15.

While PS structures are a technically useful tool for capturing default reasoning, it is not so clear where the sequence of probabilities is coming from. Under what circumstances would an agent use a sequence of probability measures to describe her uncertainty? In Chapter 11, we shall see a context in which such sequences arise naturally.

8.4.2 Using Possibility Measures, Ranking Functions, and Preference Orders

Taking φ → ψ to hold iff μ(ψ | φ) > μ( ψ | φ) does not work, in the sense that it does not satisfy some properties that seem important in the context of default reasoning. Belief functions and lower probabilities fare no better than probability measures; again, they satisfy LLE, RW, and REF, but not AND, OR, or CM. Indeed, since probability measures are a special case of belief functions and sets of probability measures, the counterexamples in the previous section apply without change. It is also possible to use sequences of belief functions or sequences of sets of probability measures, just as in PS structures. This in fact would result in the desired properties, although I do not go through the exercise of showing that here. More interestingly, possibility measures, ranking functions, and partial preorders have the desired properties without the need to consider sequences. The idea is to take φ → ψ to hold if ψ is believed conditional on φ. The reason this works is essentially because these representations of uncertainty all satisfy Pl4.

The formal definitions are just the obvious analogue of the definitions in the case of probability.

If M = (W, Poss, π) is a simple possibility structure, then
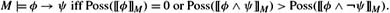
If M = (W, κ, π) is a simple ranking structure, then
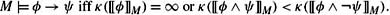
Finally, if M = (W, ≽, π) is a simple preferential structure, then

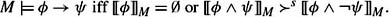
Theorem 8.4.5

Let Σ be a finite set of formulas in ^def. The following are equivalent:

Σ ⊢_P φ → ψ,
Σ ⊩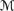_^poss φ → ψ,
Σ ⊩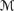_^rank φ → ψ,
Σ ⊩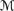_^pref φ → ψ,
Σ ⊩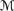_^tot φ → ψ.

Proof Soundness follows from Theorem 8.4.10. However, it is again straightforward to provide a direct proof. I show that the AND rule is sound for possibility measures here, and I leave the remaining parts of the soundness proof as an exercise (Exercise 8.23). Suppose that M = (W, Poss, π) is a possibility structure, M ⊨ φ → ψ₁, and M ⊨ φ → ψ₂. If Poss(〚φ〛_M) = 0, then it is immediate that M ⊨ φ → (ψ₁ ∧ ψ₂). So suppose that Poss(〚φ〛_M) > 0. Let U_j = 〚φ ∧ ψ_j〛_M and V_j = 〚φ ∧ ψ_j〛_M for j = 1, 2. Note that U₁ ∪ V₁ = U₂ ∪ V₂ = 〚φ〛_M. Suppose that Poss(U₁ ∩ U₂) = α, Poss(U₁ ∩ V₂) = β, Poss(V₁ ∩ U₂) = γ, and Poss(V₁ ∩ V₂) = δ. Since U₁ ∪ V₁ = U₂ ∪ V₂, it easily follows that (U₁ ∩ U₂) ∪ (U₁ ∩ V₂) = U₁ (Exercise 8.23). Thus, Poss(U₁) = max(α, β). Similarly, Poss(V₁) = max(γ, δ), Poss(U₂) = max(α, γ), and Poss(V₂) = max(β, δ). Since Poss(U_j) > Poss(V_j) for j = 1, 2, max(α, β) > max(γ, δ) and max(α, γ) > max(β, δ). It easily follows that α > max(β, γ, δ) (Exercise 8.23). Thus, Poss(U₁ ∩ U₂) > Poss(V₁ ∪ V₂), which means that Poss(〚φ ∧ ψ₁ ∧ ψ₂〛_M) > Poss(〚φ ∧ (ψ₁ ∧ ψ₂)〛_M). Thus, M ⊨ φ → (ψ₁ ∧ ψ₂), as desired.

Again, completeness follows from Theorems 8.4.14 and 8.4.15.

Recall that one interpretation of ranking functions is that they represent order-of-magnitude reasoning. That is, given a ranking function κ, there is a probability measure μ_κ such that if κ(U) = k, then μ_κ(U) is roughly ∊^k for some infinitesimal ∊. With this interpretation, κ(〚φ ∧ ψ〛_M) < κ(〚φ ∧ ψ〛_M) if μ(〚ψ〛_M | 〚φ〛_M) > 1 − ∊. This is another way of understanding the observation made in Section 8.4.1: although giving semantics to defaults in this way using a standard ∊ does not satisfy the axioms of P (AND, OR, and CM all fail), this approach does work if ∊ is an infinitesimal.

Theorem 8.4.5 provides further evidence that ^def is a relatively weak language. For example, it cannot distinguish total preferential structures from arbitrary preferential structures; the same axioms (in ^def) characterize both. Roughly speaking, P is the "footprint" of default reasoning on the language ^def. Since ^def is not a very expressive language, the footprints of the various semantic approaches are indistinguishable. By way of contrast, the language defined in Section 7.5 can distinguish (some of) these approaches, as can the conditional logic that will be defined in Section 8.6. Futher distinctions can be made with first-order conditional logic; see Section 10.4.

The approaches for giving semantics to ^def that we have considered so far take the view that φ → ψ means "if φ then ψ is very likely" or, perhaps better, "ψ is believed given φ." However, there is another semantics that focuses more on interpreting φ → ψ as "if φ, then normally ψ." This is perhaps best seen in the context of preferential structures. Suppose that ≽ is taken to define a normality (pre)ordering. That is, w ≽ w′ means that w is more "normal" than w′. For example, a world where bird ∧ fly holds might be viewed as more normal than one where bird ∧ fly holds. Given a simple preferential structure M = (W, ≽, π) and a set U ⊆ W, define best_M(U) to be the most normal worlds in U (according to the preorder ≽ in M). Since ≽ in general is a partial preorder, the formal definition is

Define a new operator →′ in simple preferential structures as follows:

The intuition behind this definition should be clear: φ →′ ψ holds in M if, in the most normal worlds where φ is true, ψ is also true. By way of contrast, notice that M ⊨ φ ⇔ ψ iff 〚φ〛_M ⊆ 〚ψ〛_M (Exercise 8.24). Thus, for φ ⇔ ψ to be valid in M, ψ must hold in all worlds where φ holds; for φ →′ ψ to be valid in M, ψ must just hold in the most normal worlds where φ holds.

Example 8.4.6

Normally, a bird flies and hence is not a penguin; normally, penguins do not fly. This property holds in the simple preferential structure M₂ = (W, ≽, π), where W ={w₁, w₂, w₃, w₄} and π is such that

(M₂, w₁) ⊨ bird ∧ fly ∧ penguin,
(M₂, w₂) ⊨ bird ∧ fly ∧ penguin,
(M₂, w₃) ⊨ bird ∧ fly ∧ penguin,
(M₂, w₄) ⊨ bird ∧ fly ∧ penguin,

and ≽ is such that w₁ ≻ w₂ ≻ w₃, w₁ ≻ w₄, and w₄ is incomparable to both w₂ and w₃. Since best_M₂(〚bird〛_M₂) ={w₁}⊆ 〚fly〛_M₂ and best_M₂(〚bird ∧ penguin〛_M₂) ={w_₂}⊆ 〚 fly〛_M₂, it follows that M₂ ⊨ bird →′ fly and M₂ ⊨ bird ∧ penguin →′ fly, aswe would hope and expect.

Although → and →′ may seem on the surface to be quite different, the following theorem shows that they are in fact equivalent:

Theorem 8.4.7

In every simple preferential structure M,

Proof See Exercise 8.25.

Of course, since → and →′ are equivalent, it follows that this semantics for →′ is also characterized by P.

8.4.3 Using Plausibility Measures

As I said before, the key reason that all these approaches for giving semantics to defaults are characterized by axiom system P is because they can all be understood as plausibility measures that satisfy Pl4. It actually turns out that Pl4 is not quite enough; one more property is needed. In this section, I make this precise. This discussion gives an excellent example of how the use of plausibility measures can help explain what is going on. The lack of structure in the plausibility framework makes it possible to understand exactly what structure is needed to get the properties of P.

The definition of → in plausibility structures is the obvious analogue of the definitions given earlier. If M = (W, ≽, Pl) is a simple measurable plausibility structure, then

Note that if Pl satisfies CPl5, this is equivalent to saying that Pl(〚ψ〛_M | 〚φ〛_M) > Pl(〚 ψ〛_M | 〚φ〛_M) if 〚φ〛_M ≠ ⊥ (the implicit assumption here is that 〚φ〛_M ∈ ′ iff 〚φ〛_M ≠ ⊥). Abusing notation somewhat, φ → ψ can be understood as a statement about conditional belief, namely, B(ψ | φ). In particular, Bφ can be viewed as an abbreviation for true → φ.

Just as with all the other representations of uncertainty, LLE, RW, and REF hold for this definition of uncertainty.

Lemma 8.4.8

All simple measurable plausibility structures satisfy LLE, RW, and REF.

Proof See Exercise 8.26. It is worth noting that REF holds in simple measurable plausibility structures because of Pl1 (recall that Pl1 says that Pl(∅) =⊥ and, by assumption, ⊥ is the minimum element with respect to ≤) and that RW holds because of Pl3 (recall that Pl3 says that Pl(U) ≤ Pl(V) if U ⊆ V).

AND, OR, and CM do not hold in general in plausibility structures. Indeed, since probability is a special case of plausibility, the counterexample given earlier in the case of probability applies here without change. This leads to an obvious question: What properties of plausibility would force AND, OR, and CM to hold? Not surprisingly, Pl4′ (and hence Pl4) turns out to be exactly what is needed to get the AND rule. This follows immediately from Proposition 8.1.1 and the following simple lemma:

Lemma 8.4.9

If M = (W, Pl, π) is a simple measurable plausibility structure such that Pl satisfies Pl4′, then the AND rule holds in M.

Proof Suppose that M ⊨ φ → ψ₁ and M ⊨ φ → ψ₂. If Pl(〚φ〛_M) = ⊥, then, by definition, M ⊨ φ → (ψ₁ ∧ ψ₂). On the other hand, if Pl(〚φ〛_M) ≠ ⊥, then Pl(〚φ ∧ ψ₁〛_M) > Pl(〚φ ∧ ψ₁〛_M) and Pl(〚φ ∧ ψ₂〛_M) > Pl(〚φ ∧ ψ₂〛_M). From Pl4′, it follows that

Thus, M ⊨ φ → (ψ₁ ∧ ψ₂), as desired.

Somewhat surprisingly, Pl4 is also just what is needed to get CM and the nonvacuous case of OR. More precisely, suppose that M = (W, Pl, π) is a simple measurable plausibility structure and that M satisfies Pl4 (and Pl1–3, of course). By Proposition 8.1.1 and Lemma 8.4.9, M satisfies the AND rule. Moreover, M also satisfies CM, and if M ⊨ φ₁ → ψ, M ⊨ φ₂ → ψ, and either Pl(〚φ₁〛_M) ≠ ⊥ or Pl(〚φ₂〛_M) ≠ ⊥, then M ⊨ (φ₁ ∨ φ₂) → ψ (Exercise 8.28). Dealing with the vacuous case of OR (where both Pl(〚φ₁〛_M) = ⊥ and Pl(〚φ₂〛_M) = ⊥) requires one more (rather innocuous) property:

Note that Pl5 holds for many, but not all, the notions of uncertainty considered so far, when viewed as plausibility measures. For example, if Poss is a possibility measure, then certainly Poss(U) = Poss(V) = 0 implies Poss(U ∪ V) = 0. The same is true for probability. On the other hand, it is not true of belief functions or inner measures. For example, it is not hard to find a belief function Bel such that Bel(U) = Bel(V) = 0 but Bel(U ∪ V) ≠ 0 (Exercise 8.29).

A plausibility measure is said to be qualitative if it satisfies Pl4 and Pl5 (as well as Pl1–3). A simple measurable plausibility structure M = (W, Pl, π) is qualitative if Pl is. Let ^qual be the class of all simple qualitative plausibility structures.

Theorem 8.4.10

If Σ is a finite set of formulas in ^def, then

Proof The soundness of LLE, RW, and CM follows from Lemma 8.4.8; the soundness of AND follows from Proposition 8.1.1 and Lemma 8.4.9. The soundness of CM and OR is left to Exercise 8.30. Again, completeness follows from Theorems 8.4.14 and 8.4.15.

Exercise 2.49 and Exercise 2.52 show that simple possibility structures, ranking structures, and preferential structures can all be viewed as simple qualitative plausibility structures. Indeed, in the remainder of this chapter, I am somewhat sloppy and view ^poss, ^rank, ^pref, and ^tot as being contained in ^qual. It follows immediately from Theorem 8.4.10 that P is sound in ^poss, ^rank, ^pref, and ^tot, since these can all be viewed as subclasses of ^qual. Properties that are valid in ^qual are bound to be valid in all of its subclasses. It is because possibility measures, ranking functions, and partial preorders can all be viewed as plausibility measures that satisfy Pl4 and Pl5 that, when used to give semantics to defaults, they satisfy all the properties in P.By way of contrast, probability measures do not satisfy Pl4, and hence the obvious way of using them to give semantics to defaults does not satisfy all the properties of P.

The alert reader may sense a problem here. Conditional probability measures do not satisfy Pl4 any more than unconditional probability measures. Yet conditional probability measures were used successfully to give semantics to defaults. What is going on here? There is no contradiction, of course. In fact, there is a way to view a conditional probability measure as a plausibility measure that satisfies Pl4, at least as far as the semantics of defaults is concerned. Given a simple measurable conditional probability structure M = (W, μ, π), define a simple plausibility structure M_μ = (W, Pl, π), where

Intuitively, Pl(U) ≤ Pl(V) if V is "almost all" of U ∪ V. It is not hard to show that there is a plausibility measure with this property (Exercise 8.31); that is, there is a set D of plausibility values and a mapping Pl : 2^W → D satisfying Pl3 and (8.1). Moreover, M_μ is qualitative and satisfies the same defaults as M.

Theorem 8.4.11

Suppose that M ∈ ^cps. Then M_μ_{p s} ∈ ^qual and M ⊨ φ → ψ iff M_μ ⊨ φ → ψ.

Proof See Exercise 8.31.

What about probability sequences? A simple PS structure can also be viewed as a plausibility structure, using much the same construction as used in the case of a conditional probability measure. Given a simple PS structure M = (W, (μ₁, μ₂, …), π), define a simple plausibility structure M_PS = (W, Pl, π) such that

Again, it is not hard to show that there is a plausibility measure with this property (Exercise 8.32) and that M_PS is qualitative and satisfies the same defaults as M.

Theorem 8.4.12

Suppose that ^ps. Then _{p s} ∈ ^qual and M ⊨ φ → ψ iff M_PS ⊨ φ → ψ.

Proof See Exercise 8.32.

Thus, Theorem 8.4.10 also explains why structures in ^ps are characterized by P; it is because they too satisfy Pl4 and Pl5. Indeed, there is a sense in which Pl4 and Pl5 completely characterize the plausibility structures that satisfy P. Roughly speaking, if P is sound for a collection of plausibility structures, then all the structures in must be qualitative. (See Exercise 8.33 for details.)

For P to be sound for a class of structures, cannot have "too many" structures—in particular, no structures that are not qualitative. For P to be complete for , it is important that have "enough" structures; if has too few structures, there may be additional properties valid in . In particular, if Σ ⊬_P φ → ψ, there must be a plausibility structure M ∈ such that M ⊨ ∊ and yet M ⊯ φ → ψ. The following weak condition suffices to ensure that has enough structures in this sense:

Definition 8.4.13

A class of simple plausibility structures is rich if, for every collection φ₁, …, φ_k, k > 1, of pairwise mutually exclusive and satisfiable propositional formulas, there is a plausibility structure M = (W, PI, π) ∈ such that

The richness requirement is quite mild. It says that does not place a priori constraints on the relative plausibilities of a collection of disjoint sets. In the case of probability, it just says that given any collection of disjoint sets A₁, …, A_k, there is a probability measure μ such that μ(A₁)> … > μ(A_k) = 0. Every representation method considered thus far (viewed as a collection of plausibility structures) can easily be shown to satisfy this richness condition.

Theorem 8.4.14

Each of ^ps, ^poss, ^rank, ^pref, ^tot, and ^qual is rich.

Proof This is almost immediate from the definitions; the details are left to Exercise 8.34. Note that I am viewing ^ps, ^poss, ^rank, ^pref, and ^tot as subsets of ^qual here, so that the richness condition as stated applies to them.

Richness is a necessary and sufficient condition to ensure that the axiom system P is complete.

Theorem 8.4.15

A set of qualitative plausibility structures is rich if and only if Σ ⊩ φ → ψ implies Σ⊢_P φ → ψ for all finite sets Σ of formulas in ^def and defaults φ → ψ.

Proof The proof that richness is necessary for completeness is not hard; see Exercise 8.35. The proof that richness is sufficient for completeness is sketched (with numerous hints) in Exercise 8.36.

To summarize, the results of this section say that for representations of uncertainty that can be associated with a subclass of plausibility structures, P is sound as long as the representation satisfies Pl4 and Pl5. Moreover, P is complete if the associated class of plausibility structures is rich, a rather mild restriction.