Interfaces

The core collection interfaces are used to manipulate collections and to pass them from one method to another. The basic purpose of these interfaces is to allow collections to be manipulated independently of the details of their representation. The core collection interfaces are the heart and soul of the Collections Framework. When you understand how to use these interfaces, you know most of what there is to know about the framework. The core collection interfaces are shown in the following figure.

Figure 123. The core collection interfaces.

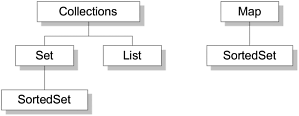
The core collection interfaces form a hierarchy: A Set is a special kind of Collection, a SortedSet is a special kind of Set, and so forth. Note also that the hierarchy consists of two distinct trees: A Map is not a true Collection.

To keep the number of core collection interfaces manageable, the Java 2 SDK doesn't provide separate interfaces for each variant of each collection type. (Immutable, fixed-size, and append-only variants are possible.) Instead, the modification operations in each interface are designated optional: A given implementation may not support some of these operations. If an unsupported operation is invoked, a collection throws an UnsupportedOperationException. Implementations are responsible for documenting which of the optional operations they support. All the Java 2 Platform's general-purpose implementations support all the optional operations.

The four basic core collection interfaces are as follows.

• The Collection interface, the root of the collection hierarchy, represents a group of objects, known as its elements. Some Collection implementations allow duplicate elements, and others do not. Some are ordered and others unordered. The Java 2 SDK doesn't provide any direct implementations of this interface but does provide implementations of more specific subinterfaces, such as Set and List. This interface is the least common denominator that all collections implement and is used to pass collections around and to manipulate them when maximum generality is desired. See the section Collection Interface (page 472).
• A Set is a collection that cannot contain duplicate elements. As you might expect, this interface models the mathematical set abstraction and is used to represent sets, such as the cards comprising a poker hand, the courses making up a student's schedule, or the processes running on a machine. See the section Set Interface (page 475).
• A List is an ordered collection (sometimes called a sequence). Lists can contain duplicate elements. The user of a List generally has precise control over where in the List each element is inserted. The user can access elements by their integer index (position). If you've used Vector, you're familiar with the general flavor of List. See the section List Interface (page 479).
• A Map is an object that maps keys to values. Maps cannot contain duplicate keys: Each key can map to at most one value. If you've used Hashtable, you're already familiar with the general flavor of Map. See the section Map Interface (page 487).

The last two core collection interfaces (SortedSet and SortedMap) are merely sorted versions of Set and Map. To understand these interfaces, you have to know how order is maintained among objects.

There are two ways to order objects: The Comparable interface provides automatic natural order on classes that implement it; the Comparator interface gives the programmer complete control over object ordering. Note that these are not core collection interfaces but rather underlying infrastructure. See the section Object Ordering (page 496).

The last two core collection interfaces are as follows.

• A SortedSet is a Set that maintains its elements in ascending order. Several additional operations are provided to take advantage of the ordering. Sorted sets are used for naturally ordered sets, such as word lists and membership rolls. See the section SortedSet Interface (page 503).
• A SortedMap, a Map that maintains its mappings in ascending key order, is the Map analog of SortedSet. Sorted maps are used for naturally ordered collections of key/value pairs, such as dictionaries and telephone directories. See the section SortedMap Interface (page 506).

Collection Interface

A Collection represents a group of objects, known as its elements. The primary use of the Collection interface is to pass around collections of objects where maximum generality is desired. For example, by convention all general-purpose collection implementations, which typically implement a subinterface of Collection, such as Set or List, have a constructor that takes a Collection argument. This constructor initializes the new Collection to contain all the elements in the specified Collection. This constructor allows the caller to create a Collection of a desired implementation type, initially containing all the elements in any given Collection, whatever its subinterface or implementation type. Suppose, for example, that you have a Collection, c, which may be a List, a Set, or another kind of Collection. The following idiom creates a new ArrayList (an implementation of the List interface), initially containing all the elements in c:

List l = new ArrayList(c); 

The Collection interface follows:

public interface Collection { 
 // Basic Operations 
 int size(); 
 boolean isEmpty(); 
 boolean contains(Object element); 
 boolean add(Object element); // Optional 
 boolean remove(Object element); // Optional 
 Iterator iterator(); 

 // Bulk Operations 
 boolean containsAll(Collection c); 
 boolean addAll(Collection c); // Optional 
 boolean removeAll(Collection c); // Optional 
 boolean retainAll(Collection c); // Optional 
 void clear(); // Optional 

 // Array Operations 
 Object[] toArray(); 
 Object[] toArray(Object a[]); 
} 

The interface does about what you'd expect, given that a Collection represents a group of objects. The interface has methods to tell you how many elements are in the collection (size, isEmpty), to check whether a given object is in the collection (contains), to add and to remove an element from the collection (add, remove), and to provide an iterator over the collection (iterator).

The add method is defined generally enough so that it makes sense for both collections that allow duplicates and those that don't. It guarantees that the Collection will contain the specified element after the call completes and returns true if the Collection changes as a result of the call. Similarly, the remove method is defined to remove a single instance of the specified element from the Collection, assuming that it contains the element, and to return true if the Collection was modified as a result.

Iterators

The object returned by the iterator method deserves special mention. It is an Iterator, which is very similar to an Enumeration, but differs in two respects.

• Iterator allows the caller to remove elements from the underlying collection during the iteration with well-defined semantics.
• Method names have been improved.

The first point is important: There was no safe way to remove elements from a collection while traversing it with an Enumeration. The semantics of this operation were ill-defined and differed from implementation to implementation.

The Iterator interface follows:

public interface Iterator { 
 boolean hasNext(); 
 Object next(); 
 void remove(); // Optional 
} 

The hasNext method is identical in function to Enumeration.hasMoreElements, and the next method is identical in function to Enumeration.nextElement. The remove method removes from the underlying Collection the last element that was returned by next. The remove method may be called only once per call to next and throws an exception if this rule is violated. Note that Iterator.remove is the only safe way to modify a collection during iteration; the behavior is unspecified if the underlying collection is modified in any other way while the iteration is in progress.

The following snippet shows you how to use an Iterator to filter a Collection, that is, to traverse the collection, removing every element that does not satisfy a condition:

static void filter(Collection c) { 
 for (Iterator i = c.iterator(); i.hasNext(); ) 
 if (!cond(i.next())) 
 i.remove(); 
} 

You should keep two things in mind when looking at this simple piece of code.

• The code is polymorphic: It works for any Collection that supports element removal, regardless of implementation. That's how easy it is to write a polymorphic algorithm under the Collections Framework!
• It would have been impossible to write this using Enumeration instead of Iterator, because there's no safe way to remove an element from a collection while traversing it with an Enumeration.

Bulk Operations

The bulk operations perform an operation on an entire Collection in a single shot. These shorthand operations can be simulated, perhaps less efficiently, by using the basic operations described previously. The bulk operations follow.

• containsAll: Returns true if the target Collection contains all the elements in the specified Collection (c).
• addAll: Adds all the elements in the specified Collection to the target Collection.
• removeAll: Removes from the target Collection all its elements that are also contained in the specified Collection.
• retainAll: Removes from the target Collection all its elements that are not also contained in the specified Collection. That is, it retains in the target Collection only those elements that are also contained in the specified Collection.
• clear: Removes all elements from the Collection.

The addAll, removeAll, and retainAll methods all return true if the target Collection was modified in the process of executing the operation.

As a simple example of the power of the bulk operations, consider the following idiom to remove all instances of a specified element, e, from a Collection, c:

c.removeAll(Collections.singleton(e)); 

More specifically, suppose that you want to remove all the null elements from a Collection:

c.removeAll(Collections.singleton(null)); 

This idiom uses Collections.singleton, which is a static factory method that returns an immutable Set containing only the specified element.

Array Operations

The toArray methods are provided as a bridge between collections and older APIs that expect arrays on input. The array operations allow the contents of a Collection to be translated into an array. The simple form with no arguments creates a new array of Object. The more complex form allows the caller to provide an array or to choose the runtime type of the output array.

For example, suppose that c is a Collection. The following snippet dumps the contents of c into a newly allocated array of Object whose length is identical to the number of elements in c:

Object[] a = c.toArray(); 

Suppose that c is known to contain only strings. The following snippet dumps the contents of c into a newly allocated array of String whose length is identical to the number of elements in c:

String[] a = (String[]) c.toArray(new String[0]); 

Set Interface

A Set is a Collection that cannot contain duplicate elements. Set models the mathematical set abstraction. The Set interface contains no methods other than those inherited from Collection. Set adds the restriction that duplicate elements are prohibited. Set also adds a stronger contract on the behavior of the equals and hashCode operations, allowing Set objects to be compared meaningfully, even if their implementation types differ. Two Set objects are equal if they contain the same elements.

The Set interface follows:

public interface Set { 
 // Basic Operations 
 int size(); 
 boolean isEmpty(); 
 boolean contains(Object element); 
 boolean add(Object element); // Optional 
 boolean remove(Object element); // Optional 
 Iterator iterator(); 

 // Bulk Operations 
 boolean containsAll(Collection c); 
 boolean addAll(Collection c); // Optional 
 boolean removeAll(Collection c); // Optional 
 boolean retainAll(Collection c); // Optional 
 void clear(); // Optional 
 // Array Operations 
 Object[] toArray(); 
 Object[] toArray(Object a[]); 
} 

The SDK contains two general-purpose Set implementations. HashSet, which stores its elements in a hash table, is the better-performing implementation. TreeSet, which stores its elements in a red-black tree, [1] guarantees the order of iteration.

[1] A red-black tree is a data structure, a kind of balanced binary tree generally regarded to be among the best. The red-black tree offers guaranteed log(n) performance for all basic operations (lookup, insert, delete) and empirically speaking, is just plain fast.

Here's a simple but useful Set idiom. Suppose that you have a Collection, c, and that you want to create another Collection containing the same elements but with all duplicates eliminated. The following one-liner does the trick:

Collection noDups = new HashSet(c); 

It works by creating a Set, which by definition cannot contain duplicates, initially containing all the elements in c. It uses the standard Collection constructor described in the section Collection Interface (page 472).

Basic Operations

The size operation returns the number of elements in the Set (its cardinality). The isEmpty method does exactly what you think it does. The add method adds the specified element to the Set if it's not already present and returns a Boolean indicating whether the element was added. Similarly, the remove method removes from the Set the specified element if it's present and returns a Boolean indicating whether the element was present. The iterator method returns an Iterator over the Set.

Here's a little program that takes the words in its argument list and prints out any duplicate words, the number of distinct words, and a list of the words with duplicates eliminated:

import java.util.*; public class FindDups { public static void main(String args[]) { Set s = new HashSet(); for (int i=0; i

Now let's run the program:

java FindDups i came i saw i left 

The following output is produced:

Duplicate: i 
Duplicate: i 
4 distinct words: [came, left, saw, i] 

Note that the code always refers to the collection by its interface type (Set) rather than by its implementation type (HashSet). This is a strongly recommended programming practice, as it gives you the flexibility to change implementations merely by changing the constructor. If either the variables used to store a collection or the parameters used to pass it around are declared to be of the collection's implementation type rather than of its interface type, all such variables and parameters must be changed to change the collection's implementation type. Furthermore, there's no guarantee that the resulting program will work; if the program uses any nonstandard operations that are present in the original implementation type but not in the new one, the program will fail. Referring to collections only by their interface keeps you honest, preventing you from using any nonstandard operations.

The implementation type of the Set in the preceding example is HashSet, which makes no guarantees as to the order of the elements in the Set. If you want the program to print the word list in alphabetical order, merely change the set's implementation type from HashSet to TreeSet. Making this trivial one-line change causes the command line in the previous example to generate the following output:

java FindDups i came i saw i left 
Duplicate word: i 
Duplicate word: i 
4 distinct words: [came, i, left, saw] 

Bulk Operations

The bulk operations are particularly well suited to Sets; when applied to sets, they perform standard set-algebraic operations. Suppose that s1 and s2 are Sets. Here's what the bulk operations do:

• s1.containsAll(s2): Returns true if s2 is a subset of s1. (Set s2 is a subset of set s1 if set s1 contains all the elements in s2.)
• s1.addAll(s2): Transforms s1 into the union of s1 and s2. (The union of two sets is the set containing all the elements contained in either set.)
• s1.retainAll(s2): Transforms s1 into the intersection of s1 and s2. (The intersection of two sets is the set containing only the elements that are common to both sets.)
• s1.removeAll(s2): Transforms s1 into the (asymmetric) set difference of s1 and s2. (For example, the set difference of s1 - s2 is the set containing all the elements found in s1 but not in s2.)

To calculate the union, intersection, or set difference of two sets nondestructively (without modifying either set), the caller must copy one set before calling the appropriate bulk operation. The resulting idioms follow:

Set union = new HashSet(s1); 
union.addAll(s2); 

Set intersection = new HashSet(s1); 
intersection.retainAll(s2); 

Set difference = new HashSet(s1); 
difference.removeAll(s2); 

The implementation type of the result Set in the preceding idioms is HashSet, which is, as already mentioned, the best all-around Set implementation in the SDK. However, any general-purpose Set implementation could be substituted.

Let's revisit the FindDups program. Suppose that you want to know which words in the argument list occur only once and which occur more than once but that you do not want any duplicates printed out repeatedly. This effect can be achieved by generating two sets, one containing every word in the argument list and the other containing only the duplicates. The words that occur only once are the set difference of these two sets, which we know how to compute. Here's how the resulting program looks:

import java.util.*; 

public class FindDups2 { 
 public static void main(String args[]) { 
 Set uniques = new HashSet(); 
 Set dups = new HashSet(); 

 for (int i = 0; i < args.length; i++) 
 if (!uniques.add(args[i])) 
 dups.add(args[i]); 

 uniques.removeAll(dups); // Destructive set-difference 

 System.out.println("Unique words: " + uniques); 
 System.out.println("Duplicate words: " + dups); 
 } 
} 

When run with the same argument list used earlier (i came i saw i left), this program yields the output:

Unique words: [came, left, saw] 
Duplicate words: [i] 

A less common set-algebraic operation is the symmetric set difference: the set of elements contained in either of two specified sets but not in both. The following code calculates the symmetric set difference of two sets nondestructively:

Set symmetricDiff = new HashSet(s1); 
symmetricDiff.addAll(s2); 
Set tmp = new HashSet(s1); 
tmp.retainAll(s2)); 
symmetricDiff.removeAll(tmp); 

Array Operations

The array operations don't do anything special for Sets beyond what they do for any other Collection. These operations are described in the section Collection Interface (page 472).

List Interface

A List is an ordered Collection, sometimes called a sequence. Lists may contain duplicate elements. In addition to the operations inherited from Collection, the List interface includes operations for the following:

• Positional access: Manipulate elements based on their numerical position in the list.
• Search: Search for a specified object in the list and return its numerical position.
• List iteration: Extend Iterator semantics to take advantage of the list's sequential nature.
• Range view: Perform arbitrary range operations on the list.

The List interface follows:

public interface List extends Collection { 
 // Positional Access 
 Object get(int index); 
 Object set(int index, Object element); // Optional 
 void add(int index, Object element); // Optional 
 Object remove(int index); // Optional 
 abstract boolean addAll(int index, Collection c);//Optional 
 // Search 
 int indexOf(Object o); 
 int lastIndexOf(Object o); 
 // Iteration 
 ListIterator listIterator(); 
 ListIterator listIterator(int index); 

 // Range-view 
 List subList(int from, int to); 
} 

The Java 2 SDK contains two general-purpose List implementations: ArrayList, which is generally the better-performing implementation, and LinkedList, which offers better performance under certain circumstances. Also, Vector has been retrofitted to implement List.

Comparison to Vector

If you've used Vector, you're already familiar with the general flavor of List. (Of course, List is an interface and Vector is a concrete implementation.) List fixes several minor API deficiencies in Vector. Commonly used Vector operations, such as elementAt and setElementAt, have been given much shorter names. When you consider that these two operations are the List analog of brackets for arrays, it becomes apparent that shorter names are highly desirable. Consider the following assignment statement:

a[i] = a[j].Times(a[k]); 

The Vector equivalent is:

v.setElementAt(v.elementAt(j).Times(v.elementAt(k)), i); 

The List equivalent is:

v.set(i, v.get(j).Times(v.get(k))); 

You may already have noticed that the set method, which replaces the Vector method setElementAt, reverses the order of the arguments so that they match the corresponding array operation. Consider this assignment statement:

beatle[5] = "Billy Preston"; 

The Vector equivalent is:

beatle.setElementAt("Billy Preston", 5); 

The List equivalent is:

beatle.set(5, "Billy Preston"); 

For consistency's sake, the add(int, Object) method, which replaces the method insertElementAt(Object, int), also reverses the order of the arguments.

The various range operations in Vector (indexOf, lastIndexOf(setSize) have been replaced by a single range-view operation (subList), which is far more powerful and consistent.

Collection Operations

The operations inherited from Collection all do about what you'd expect them to do, assuming that you're already familiar with them from Collection. If you're not familiar with them, now would be a good time to read the section Interfaces (page 470). The remove operation always removes the first occurrence of the specified element from the list. The add and addAll operations always append the new element(s) to the end of the list. Thus, the following idiom concatenates one list to another:

list1.addAll(list2); 

Here's a nondestructive form of this idiom, which produces a third List consisting of the second list appended to the first:

List list3 = new ArrayList(list1); 
list3.addAll(list2); 

Note that the idiom, in its nondestructive form, takes advantage of ArrayList's standard Collection constructor.

Like the Set interface, List strengthens the requirements on the equals and hashCode methods so that two List objects can be compared for logical equality without regard to their implementation classes. Two List objects are equal if they contain the same elements in the same order.

Positional Access and Search Operations

The basic positional access operations (get, set, add, and remove) behave just like their longer-named counterparts in Vector (elementAt, setElementAt, insertElementAt, and removeElementAt), with one noteworthy exception. The set and the remove operations return the old value that is being overwritten or removed; the counterparts in Vector (setElementAt and removeElementAt) return nothing (void). The search operations indexOf and lastIndexOf behave exactly like the identically named operations in Vector.

The addAll(int, Collection) operation inserts all the elements of the specified Collection, starting at the specified position. The elements are inserted in the order they are returned by the specified Collection's iterator. This call is the positional access analog of Collection's addAll operation.

Here's a little function to swap two indexed values in a List. It should look familiar from Programming 101 (assuming you stayed awake):

private static void swap(List a, int i, int j) { 
 Object tmp = a.get(i); 
 a.set(i, a.get(j)); 
 a.set(j, tmp); 
} 

Of course, there's one big difference. This is a polymorphic algorithm: It swaps two elements in any List, regardless of its implementation type. "Big deal," you say, "what's it good for?" Funny you should ask. Take a look at this:

public static void shuffle(List list, Random rnd) { 
 for (int i=list.size(); i>1; i--) 
 swap(list, i-1, rnd.nextInt(i)); 
} 

This algorithm, which is included in the Java 2 SDK's Collections class, randomly permutes the specified List, using the specified source of randomness. It's a bit subtle: It runs up the list from the bottom, repeatedly swapping a randomly selected element into the current position. Unlike most naive attempts at shuffling, it's fair (all permutations occur with equal likelihood, assuming an unbiased source of randomness) and fast (requiring exactly list.size()-1 iterations). The following short program uses this algorithm to print the words in its argument list in random order:

import java.util.*; public class Shuffle { public static void main(String args[]) { List l = new ArrayList(); for (int i=0; i

In fact, we can make this program even shorter and faster. The Arrays class has a static factory method, asList, that allows an array to be viewed as a List. This method does not copy the array; changes in the List write through to the array, and vice versa. The resulting List is not a general-purpose List implementation in that it doesn't implement the (optional) add and remove operations: Arrays are not resizable. Taking advantage of Arrays.asList and calling an alternative form of shuffle that uses a default source of randomness, you get the following tiny program, whose behavior is identical to that of the previous program:

import java.util.*; 

public class Shuffle { 
 public static void main(String args[]) { 
 List l = Arrays.asList(args); 
 Collections.shuffle(l); 
 System.out.println(l); 
 } 
} 

Iterators

As you'd expect, the Iterator returned by List's iterator operation returns the elements of the list in proper sequence. List also provides a richer iterator, called a ListIterator, that allows you to traverse the list in either direction, to modify the list during iteration, and to obtain the current position of the iterator. The ListIterator interface follows, including the three methods it inherits from Iterator:

public interface ListIterator extends Iterator { 
 boolean hasNext(); 
 Object next(); 

 boolean hasPrevious(); 
 Object previous(); 

 int nextIndex(); 
 int previousIndex(); 

 void remove(); // Optional 
 void set(Object o); // Optional 
 void add(Object o); // Optional 
} 

The three methods that ListIterator inherits from Iterator (hasNext, next, and remove) are intended to do exactly the same thing in both interfaces. The hasPrevious and the previous operations are exact analogs of hasNext and next. The former operations refer to the element before the (implicit) cursor, whereas the latter refer to the element after the cursor. The previous operation moves the cursor backward, whereas next moves it forward.

Here's the standard idiom for iterating backward through a list:

for (ListIterator i = l.listIterator(l.size()); 
 l.hasPrevious(); ) { 
 Foo f = (Foo) l.previous(); 
 ... 
} 

Note the argument to listIterator in the preceding idiom. The List interface has two forms of the listIterator method. The form with no arguments returns a ListIterator positioned at the beginning of the list; the form with an int argument returns a ListIterator positioned at the specified index. The index refers to the element that would be returned by an initial call to next. An initial call to previous would return the element whose index was index-1. In a list of length n, there are n+1 valid values for index, from 0 to n, inclusive.

Intuitively speaking, the cursor is always between two elements: the one that would be returned by a call to previous and the one that would be returned by a call to next. The n+1 valid index values correspond to the n+1 gaps between elements, from the gap before the first element to the gap after the last one. The following diagram shows the five possible cursor positions in a list containing four elements.

Figure 124. Five possible cursor positions in a list with four elements.

Calls to next and previous can be intermixed, but you have to be a bit careful. After a sequence of calls to next, the first call to previous returns the same element as the last call to next. Similarly, the first call to next after a sequence of calls to previous returns the same element as the last call to previous.

It should come as no surprise that the nextIndex method returns the index of the element that would be returned by a subsequent call to next and that previousIndex returns the index of the element that would be returned by a subsequent call to previous. These calls are typically used either to report the position where something was found or to record the position of the ListIterator so that another ListIterator with identical position can be created.

It should also come as no surprise that the number returned by nextIndex is always one greater than the number returned by previousIndex. This implies the behavior of the two boundary cases: A call to previousIndex when the cursor is before the initial element returns -1, and a call to nextIndex when the cursor is after the final element returns list.size(). To make all this concrete, here's a possible implementation of List.indexOf:

public int indexOf(Object o) { 
 for (ListIterator i = listIterator(); i.hasNext(); ) { 
 if (o==null ? i.next()==null : o.equals(i.next())) { 
 return i.previousIndex(); 

 return -1; // Object not found **this line is online!** 
} 

Note that the indexOf method returns i.previousIndex(), although it is traversing the list in the forward direction. The reason is that i.nextIndex() would return the index of the element that we are about to examine, and we want to return the index of the element we just examined.

The Iterator interface provides the remove operation to remove from the Collection the last element returned by next. For ListIterator, this operation removes the last element returned by next or previous. The ListIterator interface provides two additional operations to modify the list: set and add. The set method overwrites the last element returned by next or previous with the specified element. The following polymorphic algorithm uses set to replace all occurrences of one specified value with another.

public void replace(List l, Object val, Object newVal) { 
 for (ListIterator i = l.listIterator(); i.hasNext(); ) 
 if (val==null ? i.next()==null : val.equals(i.next())) 
 i.set(newVal); 
} 

The only bit of trickiness in this example is the equality test between val and i.next. We have to special-case an old value of null in order to prevent a NullPointerException.

The add method inserts a new element into the list, immediately before the current cursor position. This method is illustrated in the following polymorphic algorithm to replace all occurrences of a specified value with the sequence of values contained in the specified list:

public static void replace(List l, Object val, List newVals) { 
 for (ListIterator i = l.listIterator(); i.hasNext(); ) { 
 if (val==null ? i.next()==null : val.equals(i.next())) { 
 i.remove(); 
 for (Iterator j= newVals.iterator(); j.hasNext(); ) 
 i.add(j.next()); 
 } 
 } 
} 

Range-View Operation

The range-view operation, subList(int fromIndex, int toIndex), returns a List view of the portion of this list whose indices range from fromIndex, inclusive, to toIndex, exclusive. This half-open range mirrors the typical for loop:

for (int i=fromIndex; i

As the term view implies, the returned List is backed by the List on which subList was called, so changes in the former List are reflected in the latter.

This method eliminates the need for explicit range operations (of the sort that commonly exist for arrays). Any operation that expects a List can be used as a range operation by passing a subList view instead of a whole List. For example, the following idiom removes a range of elements from a list:

list.subList(fromIndex, toIndex).clear(); 

Similar idioms may be constructed to search for an element in a range:

int i = list.subList(fromIndex, toIndex).indexOf(o); 
int j = list.subList(fromIndex, toIndex).lastIndexOf(o); 

Note that the preceding idioms return the index of the found element in the subList, not the index in the backing List.

Any polymorphic algorithm that operates on a List, such as the replace and shuffle examples, works with the List returned by subList.

Here's a polymorphic algorithm whose implementation uses subList to deal a hand from a deck. That is to say, it returns a new List (the "hand") containing the specified number of elements taken from the end of the specified List (the "deck"). The elements returned in the hand are removed from the deck:

public static List dealHand(List deck, int n) { 
 int deckSize = deck.size(); 
 List handView = deck.subList(deckSize-n, deckSize); 
 List hand = new ArrayList(handView); 
 handView.clear(); 
 return hand; 
} 

Note that this algorithm removes the hand from the end of the deck. For many common List implementations, such as ArrayList, the performance of removing elements from the end of the list is substantially better than that of removing elements from the beginning. [1]

[1] The literal-minded might say that this program deals from the bottom of the deck, but we prefer to think that the computer is holding the deck upside down.

Although the subList operation is extremely powerful, some care must be exercised when using it. The semantics of the List returned by subList become undefined if elements are added to or removed from the backing List in any way other than via the returned List. Thus, it's highly recommended that you use the List returned by subList only as a transient object: to perform one or a sequence of range operations on the backing List. The longer you use the subList object, the greater the probability that you'll compromise it by modifying the backing List directly or through another subList object. Note that it is legal to modify a sublist of a sublist and to continue using the original sublist.

Algorithms

Most of the polymorphic algorithms in the Collections class apply specifically to List. Having all these algorithms at your disposal makes it very easy to manipulate lists. Here's a summary of these algorithms, which are described in more detail in the section Algorithms (page 515):

• sort(List): Sorts a List, using a merge sort algorithm, which provides a fast, stable sort. (A stable sort is one that does not reorder equal elements.)
• shuffle(List): Randomly permutes the elements in a List.
• reverse(List): Reverses the order of the elements in a List.
• fill(List, Object): Overwrites every element in a List with the specified value.
• copy(List dest, List src): Copies the source List into the destination List.
• binarySearch(List, Object): Searches for an element in an ordered List, using the binary search algorithm.

Map Interface

A Map is an object that maps keys to values. A map cannot contain duplicate keys: Each key can map to at most one value. The Map interface follows:

public interface Map { 
 // Basic Operations 
 Object put(Object key, Object value); 
 Object get(Object key); 
 Object remove(Object key); 
 boolean containsKey(Object key); 
 boolean containsValue(Object value); 
 int size(); 
 boolean isEmpty(); 

 // Bulk Operations 
 void putAll(Map t); 
 void clear(); 

 // Collection Views 
 public Set keySet(); 
 public Collection values(); 
 public Set entrySet(); 

 // Interface for entrySet elements 
 public interface Entry { 
 Object getKey(); 
 Object getValue(); 
 Object setValue(Object value); 
 } 
} 

The Java 2 SDK contains two new general-purpose Map implementations. HashMap, which stores its entries in a hash table, is the better-performing implementation. TreeMap, which stores its entries in a red-black tree, guarantees the order of iteration. Also, Hashtable has been retrofitted to implement Map.

Comparison to Hashtable

If you've used Hashtable, you're already familiar with the general flavor of Map. (Of course, Map is an interface, whereas Hashtable is a concrete implementation.) Here are the major differences.

• Map provides Collection views instead of direct support for iteration via Enumeration objects. Collection views greatly enhance the expressiveness of the interface, as discussed later in this section.
• Map allows you to iterate over keys, values, or key-value pairs; Hashtable does not provide the third option.
• Map provides a safe way to remove entries in the midst of iteration; Hashtable does not.

Further, Map fixes a minor deficiency in the Hashtable interface. Hashtable has a method called contains, which returns true if the Hashtable contains a given value. Given its name, you'd expect this method to return true if the Hashtable contained a given key, as the key is the primary access mechanism for a Hashtable. The Map interface eliminates this source of confusion by renaming the method containsValue. Also, this improves the consistency of the interface: containsValue parallels containsKey nicely.

Basic Operations

The basic operations (put, get, remove, containsKey, containsValue, size, and isEmpty) behave exactly like their counterparts in Hashtable. Here's a simple program to generate a frequency table of the words found in its argument list. The frequency table maps each word to the number of times it occurs in the argument list:

import java.util.*; public class Freq { private static final Integer ONE = new Integer(1); public static void main(String args[]) { Map m = new HashMap(); // Initialize frequency table from command line for (int i=0; i

The only thing even slightly tricky about this program is the second argument of the put statement. That argument is a conditional expression that has the effect of setting the frequency to one if the word has never been seen before or one more than its current value if the word has already been seen. Try running this program with the command

java Freq if it is to be it is up to me to delegate 

The program yields the following output:

8 distinct words: 
{to=3, me=1, delegate=1, it=2, is=2, if=1, be=1, up=1} 

Suppose that you'd prefer to see the frequency table in alphabetical order. All you have to do is change the implementation type of the Map from HashMap to TreeMap. Making this four-character change causes the program to generate the following output from the same command line:

8 distinct words: 
{be=1, delegate=1, if=1, is=2, it=2, me=1, to=3, up=1} 

Are interfaces cool, or what?

Like the Set and the List interfaces, Map strengthens the requirements on the equals and hashCode methods so that two Map objects can be compared for logical equality without regard to their implementation types. Two Map objects are equal if they represent the same key-value mappings.

By convention, all Map implementations provide constructors that take a Map object and initialize the new Map to contain all the key-value mappings in the specified Map. This standard Map constructor is entirely analogous to the standard collection constructor for Collection implementations. The caller can create a Map of a desired implementation type that initially contains all the mappings in another Map, regardless of the other Map's implementation type. For example, suppose that you have a Map named m. The following one-liner creates a new HashMap initially containing all the same key-value mappings as m:

Map copy = new HashMap(m); 

Bulk Operations

The clear operation does exactly what you think it does: It removes all the mappings from the Map. The putAll operation is the Map analog of the Collection interface's addAll operation. In addition to its obvious use of dumping one Map into another, it has a second, more subtle use. Suppose that a Map is used to represent a collection of attribute-value pairs; the putAll operation, in combination with the standard Map constructor, provides a neat way to implement attribute map creation with default values. Here's a static factory method demonstrating this technique:

Map newAttributeMap(Map defaults, Map overrides) { 
 Map result = new HashMap(defaults); 
 result.putAll(overrides); 
 return result; 
} 

Collection Views

The Collection view methods allow a Map to be viewed as a Collection in three ways:

• keySet: The Set of keys contained in the Map.
• values: The Collection of values contained in the Map. This Collection is not a Set, as multiple keys can map to the same value.
• entrySet: The Set of key-value pairs contained in the Map. The Map interface provides a small nested interface called Map.Entry, the type of the elements in this Set.

The Collection views provide the only means to iterate over a Map. Here's an example illustrating the standard idiom for iterating over the keys in a Map:

for (Iterator i=m.keySet().iterator(); i.hasNext(); ) { 
 System.out.println(i.next()); 
} 

The idiom for iterating over values is analogous. Here's the idiom for iterating over key-value pairs:

for (Iterator i=m.entrySet().iterator(); i.hasNext(); ) { 
 Map.Entry e = (Map.Entry) i.next(); 
 System.out.println(e.getKey() + ": " + e.getValue()); 
} 

At first, many people worry that these idioms might be slow because the Map has to create a new Collection object each time a Collection view operation is called. Rest easy: There's no reason that a Map can't always return the same object each time it is asked for a given Collection view. This is precisely what all the Java 2 SDK's Map implementations do.

With all three Collection views, calling an Iterator's remove operation removes the associated entry from the backing Map, assuming that the backing map supports element removal to begin with. With the entrySet view, it is also possible to change the value associated with a key, by calling a Map.Entry's setValue method during iteration, again assuming that the Map supports value modification to begin with. Note that these are the only safe ways to modify a Map during iteration; the behavior is unspecified if the underlying Map is modified in any other way while the iteration is in progress.

The Collection views support element removal in all its many forms: the remove, removeAll, retainAll, and clear operations, as well as the Iterator.remove operation. (Yet again, this assumes that the backing Map supports element removal.)

The Collection views do not support element addition under any circumstances. It would make no sense for the keySet and the values views, and it's unnecessary for the entrySet view, as the backing Map's put and putAll provide the same functionality.

Fancy Uses of Collection Views: Map Algebra

When applied to the Collection views, the bulk operations (containsAll, removeAll, and retainAll) are a surprisingly potent tool. Suppose that you want to know whether one Map is a submap of another, that is, whether the first Map contains all the key-value mappings in the second. The following idiom does the trick:

if (m1.entrySet().containsAll(m2.entrySet())) { 
 ... 
} 

Along similar lines, suppose that you want to know whether two Map objects contain mappings for all the same keys:

if (m1.keySet().equals(m2.keySet())) { 
 ... 
} 

Suppose that you have a map representing a collection of attribute-value pairs and two sets representing required attributes and permissible attributes. (The permissible attributes include the required attributes.) The following snippet determines whether the attribute map conforms to these constraints and prints a detailed error message if it doesn't:

boolean valid = true; 
Set attributes = attributeMap.keySet(); 
if(!attributes.containsAll(requiredAttributes)) { 
 Set missing = new HashSet(requiredAttributes); 
 missing.removeAll(attributes); 
 System.out.println("Missing attributes: " + missing); 
 valid = false; 
} 

if (!permissibleAttributes.containsAll(attributes)) { 
 illegal = new HashSet(attributes); 
 illegal.removeAll(permissibleAttributes)); 
 System.out.println(Illegal attributes: " + illegal); 
 valid = false; 
} 

if (valid) { 
 System.out.println("OK"); 
} 

Suppose that you want to know all the keys common to two Map objects:

Set commonKeys = new HashSet(a.keySet()); 
commonKeys.retainAll(b.keySet); 

A similar idiom gets you the common values and the common key-value pairs. Extra care is needed if you get the common key-value pairs, as the elements of the resulting Set, which are Map.Entry objects, may become invalid if the Map is modified.

All the idioms presented thus far have been nondestructive; that is, they don't modify the backing Map. Here are a few that do. Suppose that you want to remove all the key-value pairs that one Map has in common with another:

m1.entrySet().removeAll(m2.entrySet()); 

Suppose that you want to remove from one Map all the keys that have mappings in another:

m1.keySet().removeAll(m2.keySet()); 

What happens when you start mixing keys and values in the same bulk operation? Suppose that you have a Map, managers, that maps each employee in a company to the employee's manager. We'll be deliberately vague about the types of the key and the value objects. It doesn't matter, so long as they're the same. Now suppose that you want to know who all the individual contributors, or nonmanagers, are. The following one-liner tells you exactly what you want to know:

Set individualContributors = new HashSet(managers.keySet()); 
individualContributors.removeAll(managers.values()); 

Suppose that you want to fire all the employees who report directly to a particular manager, Herbert:

Employee herbert = ... ; 
managers.values().removeAll(Collections.singleton(herbert)); 

Note that this idiom makes use of Collections.singleton, a static factory method that returns an immutable Set with the single, specified element.

Once you've done this, you may have a bunch of employees whose managers no longer work for the company (if any of Herbert's direct reports were themselves managers). The following code tells you all the employees whose manager no longer works for the company:

Map m = new HashMap(managers); 
m.values().removeAll(managers.keySet()); 
Set slackers = m.keySet(); 

This example is a bit tricky. First, it makes a temporary copy of the Map, and it removes from the temporary copy all entries whose (manager) value is a key in the original Map. Remember that the original Map has an entry for each employee. Thus, the remaining entries in the temporary Map comprise all the entries from the original Map whose (manager) values are no longer employees. The keys in the temporary copy, then, represent precisely the employees we're looking for.

There are many, many more idioms like the ones contained in this section, but it would be impractical and tedious to list them all. Once you get the hang of it, it's not that difficult to come up with the right one when you need it.

Multimaps

A multimap is like a map but can map each key to multiple values. The Collections Framework doesn't include an interface for multimaps, because they aren't used all that commonly. It's a fairly simple matter to use a Map whose values are List objects as a multimap. This technique is demonstrated in the next code example, which reads a dictionary containing one word (all lowercase) per line and prints out all the permutation groups that meet a size criterion. A permutation group is a bunch of words, all of which contain exactly the same letters but in a different order. The program takes two arguments on the command line: the name of the dictionary file and the minimum size of permutation group to print out. Permutation groups containing fewer words than the specified minimum are not printed.

There is a standard trick for finding permutation groups: For each word in the dictionary, alphabetize the letters in the word (that is, reorder the word's letters into alphabetical order) and put an entry into a multimap, mapping the alphabetized word to the original word. For example, the word "bad" causes an entry mapping "abd" into "bad" to be put into the multimap. A moment's reflection will show that all the words to which any given key maps form a permutation group. It's a simple matter to iterate over the keys in the multimap, printing out each permutation group that meets the size constraint.

The following program is a straightforward implementation of this technique. The only tricky part is the alphabetize method, which returns a string containing the same characters as its argument, in alphabetical order. This routine (which has nothing to do with the Collections Framework) implements a slick bucket sort. It assumes that the word being alphabetized consists entirely of lowercase alphabetic characters:

import java.util.*; import java.io.*; public class Perm { public static void main(String[] args) { int minGroupSize = Integer.parseInt(args[1]); // Read words from file and put into simulated multimap Map m = new HashMap(); try { BufferedReader in = new BufferedReader(new FileReader(args[0])); String word; while((word = in.readLine()) != null) { String alpha = alphabetize(word); List l = (List) m.get(alpha); if (l==null) m.put(alpha, l=new ArrayList()); l.add(word); } } catch(IOException e) { System.err.println(e); System.exit(1); } // Print all permutation groups above size threshold for (Iterator i = m.values().iterator(); i.hasNext(); ) { List l = (List) i.next(); if (l.size() >= minGroupSize) System.out.println(l.size() + ": " + l); } } private static String alphabetize(String s) { int count[] = new int[256]; int len = s.length(); StringBuffer result = new StringBuffer(len); for (int i=0; i

Running the program on an 80,000-word dictionary takes about 16 seconds on an aging UltraSparc 1. With a minimum permutation group size of eight, it produces the following output:

 9: [estrin, inerts, insert, inters, niters, nitres, sinter, 
 triens, trines] 

 8: [carets, cartes, caster, caters, crates, reacts, recast, 
 traces] 

 9: [capers, crapes, escarp, pacers, parsec, recaps, scrape, 
 secpar, spacer] 

 8: [ates, east, eats, etas, sate, seat, seta, teas] 
12: [apers, apres, asper, pares, parse, pears, prase, presa, 
 rapes, reaps, spare, spear] 

 9: [anestri, antsier, nastier, ratines, retains, retinas, 
 retsina, stainer, stearin] 

10: [least, setal, slate, stale, steal, stela, taels, tales, 
 teals, tesla] 

 8: [arles, earls, lares, laser, lears, rales, reals, seral] 

 8: [lapse, leaps, pales, peals, pleas, salep, sepal, spale] 

 8: [aspers, parses, passer, prases, repass, spares, sparse, 
 spears] 

 8: [earings, erasing, gainers, reagins, regains, reginas, 
 searing, seringa] 

11: [alerts, alters, artels, estral, laster, ratels, salter, 
 slater, staler, stelar, talers] 

 9: [palest, palets, pastel, petals, plates, pleats, septal, 
 staple, tepals] 

 8: [enters, nester, renest, rentes, resent, tenser, ternes, 
 treens] 

 8: [peris, piers, pries, prise, ripes, speir, spier, spire] 

Many of these words seem a bit bogus, but that's not the program's fault; they're in the dictionary file.

Object Ordering

A List l may be sorted as follows:

Collections.sort(l); 

If the list consists of String elements, it will be sorted into alphabetical order. If it consists of Date elements, it will be sorted into chronological order. How does the Java programming language know how to do this? It's magic. Well, no. String and Date both implement the Comparable interface, which provides a natural ordering for a class, allowing objects of that class to be sorted automatically. The following table summarizes the Java 2 SDK classes that implement Comparable.

Table 62. Java 2 SDK Implementing Comparable

Class	Natural Ordering
Byte	Signed numerical
Character	Unsigned numerical
Long	Signed numerical
Integer	Signed numerical
Short	Signed numerical
Double	Signed numerical
Float	Signed numerical
BigInteger	Signed numerical
BigDecimal	Signed numerical
File	System-dependent lexicographic on path name
String	Lexicographic
Date	Chronological
CollationKey	Locale-specific lexicographic

If you try to sort a list whose elements do not implement Comparable, Collections.sort(list) will throw a ClassCastException. Similarly, if you try to sort a list whose elements cannot be compared to one another, Collections.sort will throw a ClassCastException. Elements that can be compared to one another are called mutually comparable. Although elements of different types can be mutually comparable, none of the SDK types listed here permit interclass comparison.

This is all you need to know about the Comparable interface if you just want to sort lists of comparable elements or to create sorted collections of them. The next section will be of interest to you if you want to implement your own Comparable type.

Writing Your Own Comparable Types

The Comparable interface consists of a single method:

public interface Comparable { 
 public int compareTo(Object o); 
} 

The compareTo method compares the receiving object with the specified object and returns a negative integer, zero, or a positive integer as the receiving object is less than, equal to, or greater than the specified object. If the specified object cannot be compared to the receiving object, the method throws a ClassCastException.

The following class representing a person's name implements Comparable:

import java.util.*; 

public class Name implements Comparable { 
 private String firstName, lastName; 

 public Name(String firstName, String lastName) { 
 if (firstName==null || lastName==null) { 
 throw new NullPointerException(); 
 } 
 this.firstName = firstName; 
 this.lastName = lastName; 
 } 

 public String firstName() {return firstName;} 

 public String lastName() {return lastName;} 

 public boolean equals(Object o) { 
 if (!(o instanceof Name)) 
 return false; 
 Name n = (Name)o; 
 return n.firstName.equals(firstName) && 
 n.lastName.equals(lastName); 
 } 

 public int hashCode() { 
 return 31*firstName.hashCode() + lastName.hashCode(); 
 } 

 public String toString() { 
 return firstName + " " + lastName; 
 } 

 public int compareTo(Object o) { 
 Name n = (Name)o; 
 int lastCmp = lastName.compareTo(n.lastName); 
 return (lastCmp!=0 ? lastCmp : 
 firstName.compareTo(n.firstName)); 
 } 
} 

To keep the example short, the class is somewhat limited: It doesn't support middle names, it demands both a first and a last name, and it is not internationalized in any way. Nonetheless, it illustrates several important points.

• Name objects are immutable. All other things being equal, immutable types are the way to go, especially for objects that will be used as elements in Sets or as keys in Maps. These collections will break if you modify their elements or keys while they're in the collection.
• The constructor checks its arguments for null. This ensures that all Name objects are well formed, so that none of the other methods will ever throw a NullPointerException.
• The hashCode method is redefined. This is essential for any class that redefines the equals method. (Equal objects must have equal hash codes.)
• The equals method returns false if the specified object is null or of an inappropriate type. The compareTo method throws a runtime exception under these circumstances. Both of these behaviors are required by the general contracts of the respective methods.
• The toString method has been redefined to print the name in human-readable form. This is always a good idea, especially for objects that will be put into collections. The various collection types' toString methods depend on the toString methods of their elements, keys, and values.

Since this section is about element ordering, let's talk more about Name's compareTo method. It implements the standard name-ordering algorithm, where last names take precedence over first names. This is exactly what you want in a natural ordering. It would be confusing if the natural ordering were unnatural!

Take a look at how compareTo is implemented, because it's quite typical. First, you cast the Object argument to the appropriate type. This throws the appropriate exception (ClassCastException) if the argument's type is inappropriate. Then you compare the most significant part of the object (in this case, the last name). Often, you can just use the natural ordering of the part's type. In this case, the part is a String, and the natural (lexicographic) ordering is exactly what's called for. If the comparison results in anything other than zero, which represents equality, you're done: You just return the result. If the most significant parts are equal, you go on to compare the next-most-significant parts. In this case, there are only two parts: first name and last name. If there were more parts, you'd proceed in the obvious fashion, comparing parts until you found two that weren't equal or you were comparing the least-significant parts, at which point you'd return the result of the comparison.

Just to show that it all works, here's a little program that builds a list of names and sorts them:

import java.util.*; 

class NameSort { 
 public static void main(String args[]) { 
 Name n[] = { 
 new Name("John", "Lennon"), 
 new Name("Karl", "Marx"), 
 new Name("Groucho", "Marx"), 
 new Name("Oscar", "Grouch") 
 }; 
 List l = Arrays.asList(n); 
 Collections.sort(l); 
 System.out.println(l); 
 } 
} 

If you run this program, here's what it prints:

[Oscar Grouch, John Lennon, Groucho Marx, Karl Marx] 

There are four restrictions on the behavior of the compareTo method, which we won't go over now because they're fairly technical and boring and are better left in the API documentation. It's really important that all classes that implement Comparable obey these restrictions, so read the documentation for Comparable if you're writing a class that implements it. Attempting to sort a list of objects that violate these restrictions has undefined behavior. Technically speaking, these restrictions ensure that the natural ordering is a total order on the objects of a class that implements it; this is necessary to ensure that sorting is well defined.

Comparators

What if you want to sort some objects in an order other than their natural order? Or what if you want to sort some objects that don't implement Comparable? To do either of these things, you'll need to provide a Comparator, an object that encapsulates an ordering. Like the Comparable interface, the Comparator interface consists of a single method:

public interface Comparator { 
 int compare(Object o1, Object o2); 
} 

The compare method compares its two arguments and returns a negative integer, zero, or a positive integer according to whether the first argument is less than, equal to, or greater than the second. If either of the arguments has an inappropriate type for the Comparator, the compare method throws a ClassCastException.

Much of what was said about Comparable applies to Comparator as well. Writing a compare method is nearly identical to writing a compareTo method, except that the former gets both objects passed in as arguments. The compare method has to obey the same four technical restrictions as Comparable's compareTo method, for the same reason: A Comparator must induce a total order on the objects it compares.

Suppose that you have a class called EmployeeRecord:

public class EmployeeRecord implements Comparable { 
 public Name name(); 
 public int empNumber(); 
 public Date hireDate(); 
 ... 
} 

Let's assume that the natural ordering of EmployeeRecord objects is Name ordering (as defined in the previous example) on employee name. Unfortunately, the boss has asked us for a list of employees in order of seniority. This means that we have to do some work but not much. Here's a program that will produce the required list:

import java.util.*; 

class EmpSort { 
 static final Comparator SENIORITY_ORDER = new Comparator() { 
 public int compare(Object o1, Object o2) { 
 EmployeeRecord r1 = (EmployeeRecord) o1; 
 EmployeeRecord r2 = (EmployeeRecord) o2; 
 return r2.hireDate().compareTo(r1.hireDate()); 
 } 
 }; 

 // Employee Database 
 static final Collection employees = ... ; 

 public static void main(String args[]) { 
 List emp = new ArrayList(employees); 
 Collections.sort(emp, SENIORITY_ORDER); 
 System.out.println(emp); 
 } 
} 

The Comparator in the program is reasonably straightforward. It casts its arguments to EmployeeRecord and relies on the natural ordering of Date applied to the hireDate accessor method. Note that the Comparator passes the hire date of its second argument to its first, rather than vice versa. The reason is that the employee who was hired most recently is least senior: Sorting in order of hire date would put the list in reverse seniority order. Another way to achieve the same effect would be to maintain the argument order but to negate the result of the comparison:

return -r1.hireDate().compareTo(r2.hireDate()); 

The two techniques are equally preferable. Use whichever looks better to you.

The Comparator in the preceding program works fine for sorting a List, but it does have one deficiency: It cannot be used to order a sorted collection, such as TreeSet, because it generates an ordering that is not compatible with equals. This means that this comparator equates objects that the equals method does not. In particular, any two employees who were hired on the same date will compare as equal. When you're sorting a List, this doesn't matter, but when you're using the Comparator to order a sorted collection, it's fatal. If you use this Comparator to insert multiple employees hired on the same date into a TreeSet, only the first one will be added to the set. The second will be seen as a duplicate element and will be ignored.

To fix this problem, simply tweak the Comparator so that it produces an ordering that is compatible with equals. In other words, tweak it so that the only elements that are seen as equal when using compare are those that are also seen as equal when compared using equals. The way to do this is to do a two-part comparison (as we did for Name), where the first part is the one that we're interested in (in this case, the hire date), and the second part is an attribute that uniquely identifies the object. In this case, the employee number is the obvious attribute. Here's the Comparator that results:

static final Comparator SENIORITY_ORDER = new Comparator() { 
 public int compare(Object o1, Object o2) { 
 EmployeeRecord r1 = (EmployeeRecord) o1; 
 EmployeeRecord r2 = (EmployeeRecord) o2; 
 int dateCmp = r2.hireDate().compareTo(r1.hireDate()); 
 if (dateCmp != 0) { 
 return dateCmp; 
 } 

 return (r1.empNumber() < r2.empNumber() ? -1 : 
 (r1.empNumber() == r2.empNumber() ? 0 : 1)); 
 } 
}; 

One last note: You might be tempted to replace the final return statement in the Comparator with the simpler

return r1.empNumber() - r2.empNumber(); 

Don't do it unless you're absolutely sure that no one will ever have a negative employee number! This trick does not work in general, as the signed integer type is not big enough to represent the difference of two arbitrary signed integers. If i is a large positive integer and j is a large negative integer, i - j will overflow and will return a negative integer. The resulting Comparator violates one of the four technical restrictions that we keep talking about (transitivity) and produces horrible, subtle bugs. This is not a purely theoretical concern; people get burned by it.

SortedSet Interface

A SortedSet is a Set that maintains its elements in ascending order, sorted according to the elements' natural order or according to a Comparator provided at SortedSet creation time. [1] In addition to the normal Set operations, the Set interface provides operations for

[1] Natural order and comparators are discussed in a previous section, Object Ordering (page 496).

• Range view: Performs arbitrary range operations on the sorted set.
• Endpoints: Returns the first or the last element in the sorted set.
• Comparator access: Returns the Comparator, if any, used to sort the set.

The SortedSet interface follows:

public interface SortedSet extends Set { 
 // Range-view 
 SortedSet subSet(Object fromElement, Object toElement); 
 SortedSet headSet(Object toElement); 
 SortedSet tailSet(Object fromElement); 

 // Endpoints 
 Object first(); 
 Object last(); 

 // Comparator access 
 Comparator comparator(); 
} 

Set Operations

The operations that SortedSet inherits from Set behave identically on sorted sets and normal sets, with two exceptions.

• The Iterator returned by the iterator operation traverses the sorted set in order.
• The array returned by toArray contains the sorted set's elements in order.

Although the interface doesn't guarantee it, the toString method of the Java 2 SDK's SortedSet implementations returns a string containing all the elements of the sorted set, in order.

Standard Constructors

By convention, all Collection implementations provide a standard constructor that takes a Collection, and SortedSet implementations are no exception. This constructor creates a SortedSet object that orders its elements according to their natural order. In addition, SortedSet implementations provide, by convention, two other standard constructors.

• One takes a Comparator and returns a new (empty) SortedSet sorted according to the specified Comparator.
• One takes a SortedSet and returns a new SortedSet containing the same elements as the given SortedSet, sorted according to the same Comparator or using the elements' natural ordering, if the specified SortedSet did too. Note that the compile-time type of the argument determines whether this constructor is invoked in preference to the ordinary Set constructor and not the runtime type!

The first of these standard constructors is the normal way to create an empty SortedSet with an explicit Comparator. The second is similar in spirit to the standard Collection constructor: It creates a copy of a SortedSet with the same ordering but with a programmer-specified implementation type.

Range-View Operations

The range-view operations are somewhat analogous to those provided by the List interface, but there is one big difference. Range views of a sorted set remain valid even if the backing sorted set is modified directly. This is feasible because the endpoints of a range view of a sorted set are absolute points in the element space rather than specific elements in the backing collection, as is the case for lists. A range view of a sorted set is really just a window onto whatever portion of the set lies in the designated part of the element space. Changes to the range view write back to the backing sorted set, and vice versa. Thus, it's okay to use range views on sorted sets for long periods of time, unlike range views on lists.

Sorted sets provide three range-view operations. The first, subSet, takes two endpoints, like subList. Rather than indices, the endpoints are objects and must be comparable to the elements in the sorted set, using the set's Comparator or the natural ordering of its elements, whichever the set uses to order itself. Like subList, the range is half open, including its low endpoint but excluding the high one.

Thus, the following one line of code tells you how many words between "doorbell" and "pickle," including "doorbell" but excluding "pickle," are contained in a SortedSet of strings called dictionary:

int count = ss.subSet("doorbell", "pickle").size(); 

Similarly, the following one-liner removes all the elements beginning with the letter "f":

dictionary.subSet("f", "g").clear(); 

A similar trick can be used to print a table telling you how many words begin with each letter:

for (char ch='a'; ch<='z'; ch++) { 
 String from = new String(new char[] {ch}); 
 String to = new String(new char[] {(char)(ch+1)}); 
 System.out.println(from + ": " + 
 dictionary.subSet(from, to).size()); 
} 

Suppose that you want to view a closed interval, which contains both its endpoints instead of an open interval. If the element type allows for the calculation of the successor of a given value in the element space, merely request the subSet from lowEndpoint to successor(highEndpoint). Although it isn't entirely obvious, the successor of a string s in String's natural ordering is s+"" (that is, s with a null character appended).

Thus, the following one-liner tells you how many words between "doorbell" and "pickle," including "doorbell" and "pickle," are contained in the dictionary:

int count = ss.subSet("doorbell", "pickle").size(); 

A similar technique can be used to view an open interval, which contains neither endpoint. The open-interval view from lowEndpoint to highEndpoint is the half-open interval from successor(lowEndpoint) to highEndpoint. To calculate the number of words between "doorbell" and "pickle," excluding both:

int count = ss.subSet("doorbell", "pickle").size(); 

The SortedSet interface contains two more range-view operations, headSet and tailSet, both of which take a single Object argument. The former returns a view of the initial portion of the backing SortedSet, up to but not including the specified object. The latter returns a view of the final portion of the backing SortedSet, beginning with the specified object and continuing to the end of the backing SortedSet. Thus, the following code allows you to view the dictionary as two disjoint "volumes" (am and nz):

SortedSet volume1 = dictionary.headSet("n"); 
SortedSet volume2 = dictionary.tailSet("n"); 

Endpoint Operations

The SortedSet interface contains operations to return the first and the last elements in the sorted set, called (not surprisingly) first and last. In addition to their obvious uses, last allows a workaround for a deficiency in the SortedSet interface. One thing you'd like to do with a SortedSet is to go into the interior of the set and to iterate forward or backward. It's easy enough to go forward from the interior: Just get a tailSet and iterate over it. Unfortunately, there's no easy way to go backward.

The following idiom obtains in a sorted set the first element that is less than a specified object o in the element space:

Object predecessor = ss.headSet(o).last(); 

This is a fine way to go one element backward from a point in the interior of a sorted set. It could be applied repeatedly to iterate backward, but this is very inefficient, requiring a lookup for each element returned.

Comparator Accessor

The SortedSet interface contains an accessor method, called comparator, that returns the Comparator used to sort the set or null if the set is sorted according to the natural order of its elements. This method is provided so that sorted sets can be copied into new sorted sets with the same ordering. This method is used by the standard SortedSet constructor, described previously.

SortedMap Interface

A SortedMap is a Map that maintains its entries in ascending order, sorted according to the keys' natural order, or according to a Comparator provided at SortedMap creation time. Natural order and Comparators are discussed in the section Object Ordering (page 496). The Map interface provides operations for the normal Map operations and for

• Range view: Performs arbitrary range operations on the sorted map
• Endpoints: Returns the first or the last key in the sorted map
• Comparator access: Returns the Comparator, if any, used to sort the map

public interface SortedMap extends Map { 
 Comparator comparator(); 
 SortedMap subMap(Object fromKey, Object toKey); 
 SortedMap headMap(Object toKey); 
 SortedMap tailMap(Object fromKey); 
 Object first(); 
 Object last(); 
} 

This interface is the Map analog of SortedSet.

Map Operations

The operations that SortedMap inherits from Map behave identically on sorted maps and normal maps, with two exceptions.

• The Iterator returned by the iterator operation on any of the sorted map's Collection views traverse the collections in order.
• The arrays returned by the Collection views' toArray operations contain the keys, values, or entries in order.

Although it isn't guaranteed by the interface, the toString method of the Collection views in all the Java 2 Platform's SortedMap implementations returns a string containing all the elements of the view, in order.

Standard Constructors

By convention, all Map implementations provide a standard constructor that takes a Map, and SortedMap implementations are no exception. This constructor creates a SortedMap object that orders its entries according to their keys' natural order. Additionally, SortedMap implementations, by convention, provide two other standard constructors.

• One takes a Comparator and returns a new (empty) SortedMap sorted according to the specified Comparator.
• One takes a SortedMap and returns a new SortedMap containing the same mappings as the given SortedMap, sorted according to the same Comparator or using the elements' natural ordering, if the specified SortedMap did too. Note that it is the compile-time type of the argument, not its runtime type, that determines whether this constructor is invoked in preference to the ordinary Map constructor!

The first of these standard constructors is the normal way to create an empty SortedMap with an explicit Comparator. The second is similar in spirit to the standard Map constructor, creating a copy of a SortedMap with the same ordering but with a programmer-specified implementation type.

Comparison to SortedSet

Because this interface is a precise Map analog of SortedSet, all the idioms and code examples in the section Object Ordering (page 496) apply to SortedSet, with only trivial modifications.