5.4 Decision Theory

The aim of decision theory is to help agents make rational decisions. Consider an agent that has to choose between a number of acts, such as whether to bet on a horse race and, if so, which horse to bet on. Are there reasonable rules to help the agent decide how to make this choice?

5.4.1 The Basic Framework

There are a number of equivalent ways of formalizing the decision process. Intuitively, a decision situation describes the objective part of the circumstance that an agent faces (i.e., the part that is independent of the tastes and beliefs of the agent). Formally, a decision situation is a tuple DS = (A, W, C), where

W is the set of possible worlds (or states of the world),
C is the set of consequences, and
A is the set of acts (i.e., functions from W to C).

An act a is simple if its range is finite. That is, a is simple if it has only finitely many possible consequences. For simplicity, I assume here that all acts are simple. (Note that this is necessarily the case if either W or C is finite, although I do not require this.) The advantage of using simple acts is that the expected utility of an act can be defined using (plausibilistic) expectation.

A decision problem is essentially a decision situation together with information about the preferences and beliefs of the agent. These tastes and beliefs are represented using a utility function and a plausibility measure, respectively. A utility function maps consequences to utilities. Intuitively, if u is the agent's utility function and c is a consequence, then u(c) measures how happy the agent would be if c occurred. That is, the utility function quantifies the preferences of the agent. Consequence c is at least as good as consequence c′ iff u(c) ≥ u(c′). In the literature, the utility function is typically assumed to be real-valued and the plausibility measure is typically taken to be a probability measure. However, assuming that the utility function is real-valued amounts to assuming (among other things) that the agent can totally order all consequences. Moreover, there is the temptation to view a consequence with utility 6 as being "twice as good" as a consequence with utility 3. This may or may not be reasonable. In many cases, agents are uncomfortable about assigning real numbers with such a meaning to utilities. Even if an agent is willing to compare all consequences, she may be willing to use only labels such as "good," "bad," or "outstanding."

Nevertheless, in many simple settings, assuming that people have real-valued utility function and a probability measure does not seem so unreasonable. In the horse race example, the worlds could represent the order in which the horses finished the race. The plausibility measure thus represents the agent's subjective estimate of the likelihood of various orders of finish. The acts correspond to possible bets (perhaps including the act of not betting at all). The consequence of a bet of $10 on Northern Dancer depends on how Northern Dancer finishes in the world. The consequence could be purely monetary (the agent wins $50 in the worlds where Northern Dancer wins the race) but could also include feelings (the agent is dejected if Northern Dancer finishes last, and he also loses $10). Of course, if the consequence includes feelings such as dejection, then it may be more difficult to assign it a numeric utility.

Formally, a (plausibilistic) decision problem is a tuple DP = (DS, ED, Pl, u), where DS = (A, W, C) is a decision situation, ED = (D₁, D₂, D₃, ⊕, ⊗) is an expectation domain, Pl : 2^W → D₁ is a plausibility measure, and u : C → D₂ is a utility function. It is occasionally useful to consider nonplausibilistic decision problems, where there is no plausibility measure. A nonplausibilistic decision problem is a tuple DP = (DS, D, u) where DS = (A, W, C) is a decision situation and u : C → D is a utility function.

5.4.2 Decision Rules

I have taken utility and probability as primitives in representing a decision problem. But decision theorists are often reluctant to take utility and probability as primitives. Rather, they take as primitive a preference order on acts, since preferences on acts are observable (by observing agents actions), while utilities and probabilities are not. However, when writing software agents that make decisions on behalf of people, it does not seem so unreasonable to somehow endow the software agent with a representation of the tastes of the human for which it is supposed to be acting. Using utilities is one way of doing this. The agent's beliefs can be represented by a probability measure (or perhaps by some other representation of uncertainty). Alternatively, the software agent can then try to learn something about the world by gathering statistics. In any case, the agent then needs a decision rule for using the utility and plausibility to choose among acts. Formally, a (nonplausibilistic) decision rule 퓓 is a function mapping (nonplausibilistic) decision problems DP to preference orders on the acts of DP. Many decision rules have been studied in the literature.

Perhaps the best-known decision rule is expected utility maximization. To explain it, note that corresponding to each act a there is a random variable u_a on worlds, where u_a(w) = u(a(w)). If u is real-valued and the agent's uncertainty is characterized by the probability measure μ, then E_μ(u_a) is the expected utility of performing act a. The rule of expected utility maximization orders acts according to their expected utility: a is considered at least as good as a′ if the expected utility of a is greater than or equal to that of a′.

There have been arguments made that a "rational" agent must be an expected utility maximizer. Perhaps the best-known argument is due to Savage. Savage assumed that an agent starts with a preference order ≼_A on a rather rich set A of acts: all the simple acts mapping some space W to a set C of consequences. He did not assume that the agents have either a probability on W or a utility function associating with each consequence in C its utility. Nevertheless, he showed that if ≼_A satisfies certain postulates, then the agent is acting as if she has a probability measure μ on W and a real-valued utility function u on C, and is maximizing expected utility; that is, a ≼_A a′ iff E_μ(u_a) ≤ E_μ(u_a′). Moreover, μ is uniquely determined by ≼_A and u is determined up to positive affine transformations. That is, if the same result holds with u replaced by u′, then there exist real values a > 0 and b such that u(c) = au′(c) + b for all consequences c. (This is because E_μ(aX + b) = aE_μ(x) + b and x ≤ y iff ax + b ≤ ay + b.)

Of course, the real question is whether the postulates that Savage assumes for ≼_A are really ones that the preferences of all rational agents should obey. Not surprisingly, this issue has generated a lot of discussion. (See the notes for references.) Two of the postulates are analogues of RAT2 and RAT3 from Section 2.2.1: ≼ is transitive and is total. While it seems reasonable to require that an agent's preferences on acts be transitive, in practice transitivity does not always hold (as was already observed in Section 2.2.1). And it is far from clear that it is "irrational" for an agent not to have a total order on the set of all simple acts. Suppose that W ={w₁, w₂, w₃}, and consider the following two acts, a₁ and a₂:

In w₁, a₁ has the consequence "live in a little pain for three years"; in w₂, a₁ results in "live for four years in moderate pain"; and in w₃, a₁ results in "live for two years with moderate pain."
In w₁, a₂ has the consequence "undergo a painful medical operation and live for only one day"; in w₂, a₂ results in "undergo a painful operation and live a pain-free life for one year"; and in w₃, a₂ results in "undergo a painful operation and live a pain-free life for five years."

These acts seem hard enough to compare. Now consider what happens if the set of worlds is extended slightly, to allow for acts that involve buying stocks. Then the worlds would also include information about whether the stock price goes up or down, and an act that results in gaining $10,000 in one world and losing $25,000 in another would have to be compared to acts involving consequences of operations. These examples all involve a relatively small set of worlds. Imagine how much harder it is to order acts when the set of possible worlds is much larger.

There are techniques for trying to elicit preferences from an agent. Such techniques are quite important in helping people decide whether or not to undergo a risky medical procedure, for example. However, the process of elicitation may itself affect the preferences. In any case, assuming that preferences can be elicited from an agent is not the same as assuming that the agent "has" preferences.

Many experiments in the psychology literature show that people systematically violate Savage's postulates. While this could be simply viewed as showing that people are irrational, other interpretations are certainly possible. A number of decision rules have been proposed as alternatives to expected utility maximization. Some of them try to model more accurately what people do; others are viewed as more normative. Just to give a flavor of the issues involved, I start by considering two well-known decision rules: maximin and minimax regret.

Maximin orders acts by their worst-case outcomes. Let worst_u(a) = min{u_a(w) : w ∈ W}; worst_u(a) is the utility of the worst-case consequence if a is chosen. Maximin prefers a to a′ if worst_u(a) ≥ worst_u(a′). Maximin is a "conservative" rule; the "best" act according to maximin is the one with the best worst-case outcome. The disadvantage of maximin is that it prefers an act that is guaranteed to produce a mediocre outcome to one that is virtually certain to produce an excellent outcome but has a very small chance of producing a bad outcome. Of course, "virtually certain" and "very small chance" do not make sense unless there is some way of comparing the likelihood of two sets. Maximin is a nonplausibilistic decision rule; it does not take uncertainty into account at all.

Minimax regret is based on a different philosophy. It tries to hedge an agent's bets, by doing reasonably well no matter what the actual world is. It is also a nonplausibilistic rule. As a first step to defining it, for each world w, let u*(w) be the sup of the outcomes in world w; that is, u*(w) = sup_a∈A u_a(w). The regret of a in world w, denoted regret_u(a, w), is u*(w) − u_a(w); that is, the regret of a in w is essentially the difference between the utility of the best possible outcome in w and the utility of performing a in w. Let regret_u(a) = sup_w∈W regret_u(a, w) (where regret_u(a) is taken to be ∞ if there is no bound on {regret_u(a, w) : w ∈ W}). For example, if regret_u(a) = 2, then in each world w, the utility of performing a in w is guaranteed to be within 2 of the utility of any act the agent could choose, even if she knew that the actual world was w. The decision rule of minimax regret orders acts by their regret and thus takes the "best" act to be the one that minimizes the maximum regret. Intuitively, this rule is trying to minimize the regret that an agent would feel if she discovered what the situation actually was: the "I wish I had done a′ instead of a" feeling.

As the following example shows, maximin, minimax regret, and expected utility maximization give very different recommendations in general:

Example 5.4.1

Suppose that W ={w₁, w₂}, = {a₁, a₂, a₃}, and μ is a probability measure on W such that μ(w₁) = 1/5 and μ(w₂) = 4/5. Let the utility function be described by the following table:

	w₁	w₂
a₁	3	3
a₂	−1	5
a₃	2	4

Thus, for example, u(a₃(w₂)) = 4. It is easy to check that E_μ(u_a₁) = 3, E_μ(u_a₂) = 3.8, and E_μ(u_a₃) = 3.6, so the expected utility maximization rule recommends a₂. On the other hand, worst_u(a₁) = 3, worst_u(a₂) =−1, and worst_u(a₃) = 2, so the maximin rule recommends a₁. Finally, regret_u(a₁) = 2, regret_u(a₂) = 4, and regret_u(a₃) = 1, so the regret minimization rule recommends a₃.

Intuitively, maximin "worries" about the possibility that the true world may be

w₁, even if it is not all that likely relative to w₂, and tries to protect against the eventuality of w₁ occurring. Although, a utility of −1 may not be so bad, if all these number are multiplied by 1,000,000—which does not affect the recommendations at all (Exercise 5.35)—it is easy to imagine an executive feeling quite uncomfortable about a loss of $1,000,000, even if such a loss is relatively unlikely and the gain in w₂ is $5,000,000. (Recall that essentially the same point came up in the discussion of RAT4 in Section 2.2.1.) On the other hand, if −1is replaced by 1.99 in the original table (which can easily be seen not to affect the recommendations), expected utility maximization starts to seem more reasonable.

Even more decision rules can be generated by using representations of uncertainty other than probability. For example, consider a set probability measures. Define so that aa′ iff E (u_a) ≥ E(u_a′). This can be seen to some extent as a maximin rule; the best act(s) according to are those whose worst-case expectation (according to the probability measures in ) are best. Indeed, if _W consists of all probability measures on W, then it is easy to show that E_W = Worst_u(a); it thus follows that defines the same order on acts as maximin (Exercise 5.36). Thus, can be viewed as a generalization of maximin. If there is no information at all about the probability measure, then the two orders agree. However, can take advantage of partial information about the probability measure. Of course, if there is complete information about the probability measure (i.e., is a singleton), then just reduces to the ordering provided by maximizing expected utility. It is also worth recalling that, as observed in Section 5.3, the ordering on acts induced by E_Bel for a belief function Bel is the same as that given by

Other orders using can be defined in a similar way:

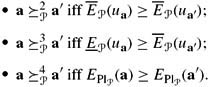
The order on acts induced by is very conservative; aa′ iff the best expected outcome according to a is no better than the worst expected outcome according to a′. The order induced by is more refined. Clearly E_Pl (u_a) ≥ E_Pl (u_a′) iff E_μ(u_a) ≥ E_μ(u_a′) for all μ ∊ . It easily follows that if aa′, then a (Exercise 5.37). The converse may not hold. For example, suppose that = {μ, μ′}, and acts a and a′ are such that E_μ(u_a) = 2, E_μ′(u_a) = 4, E_μ(u_a′) = 1, and E_μ′(u_a′) = 3. Then E(u_a) = 2, E(u_a) = 4, E(u_a′) = 1, and E(u_a′) = 3, so a and a′ are incomparable according to , yet a.

Given this plethora of decision rules, it would be useful to have one common framework in which to make sense of them all. The machinery of expectation domains developed in the previous section helps.

5.4.3 Generalized Expected Utility

There is a sense in which all of the decision rules mentioned in Section 5.4.2 can be viewed as instances of generalized expected utility maximization, that is, utility maximization with respect to plausibilistic expectation, defined using (5.14) for some appropriate choice of expectation domain. The goal of this section is to investigate this claim in more depth.

Let GEU (generalized expected utility) be the decision rule that uses (5.14). That is, if DP = (DS, ED, Pl, u), then GEU(DP) is the preference order ≼ such that a ≼ a′ iff E_{Pl, ED}(u_a) ≤ E_{Pl, ED}(u_a′). The following result shows that GEU can represent any preference order on acts:

Theorem 5.4.2

Given a decision situation DS = (A, W, C) and a partial preorder ≼_A on A, there exists an expectation domain ED = (D₁, D₂, D₃, ⊕, ⊗), a plausibility measure Pl : W → D₁, and a utility function u : C → D₂ such that GEU(DP) =≼_A, where DP = (DS, ED, Pl, u) (i.e., E_{Pl, ED}(u_a) ≤ E_{Pl, ED}(u_a′) iff a ≼_A a′).

Proof See Exercise 5.38.

Theorem 5.4.2 can be viewed as a generalization of Savage's result. It says that, whatever the agent's preference order on acts, the agent can be viewed as maximizing expected plausibilistic utility with respect to some plausibility measure and utility function. Unlike Savage's result, the plausibility measure and utility function are not unique in any sense.

The key idea in the proof of Theorem 5.4.2 is to construct D₃ so that its elements are expected utility expressions. The order ≤₃ on D₃ then mirrors the preference order ≼_A on A. This flexibility in defining the order somewhat undercuts the interest in Theorem 5.4.2. However, just as in the case of plausibility measures, this flexibility has some advantages. In particular, it makes it possible to understand exactly which properties of the plausibility measure and the expectation domain (in particular, ⊕ and ⊗) are needed to capture various properties of preferences, such as those characterized by Savage's postulates. Doing this is beyond the scope of the book (but see the notes for references). Instead, I now show that GEU is actually a stronger representation tool than this theorem indicates. It turns out that GEU can represent not just orders on actions, but the decision process itself.

Theorem 5.4.2 shows that for any preference order ≼_A on the acts of A, there is a decision problem DP whose set of acts is A such that GEU(DP) =≼_A. What I want to show is that, given a decision rule 퓓, GEU can represent 퓓 in the sense that there exists an expectation domain (in particular, a choice of ⊕ and ⊗) such that GEU (DP) = 퓓(DP) for all decision problems DP. Thus, the preference order on acts given by 퓓 is the same as that derived from GEU.

The actual definition of representation is a little more refined, since I want to be able to talk about a plausibilistic decision rule (like maximizing expected utility) representing a nonplausibilistic decision rule (like maximin). To make this precise, a few definitions are needed.

Two decision problems are congruent if they agree on the tastes and (if they are both plausibilistic decision problems) the beliefs of the agent. Formally, DP₁ and DP₂ are congruent if they involve the same decision situation, the same utility function, and (where applicable) the same plausibility measure. Note, in particular, that if DP₁ and DP₂ are both nonplausibilistic decision problems, then they are congruent iff they are identical. However, if they are both plausibilistic, it is possible that they use different notions of ⊕ and ⊗ in their expectation domains.

A decision-problem transformation τ maps decision problems to decision problems. Given two decision rules 퓓₁ and 퓓₂, 퓓₁ represents 퓓₂ iff there exists a decision-problem transformation τ such that, for all decision problems DP in the domain of 퓓₂, the decision problem τ(DP) is in the domain of 퓓₁, τ(DP) is congruent to DP, and DR₁(τ(DP)) = DR₂(DP). Intuitively, this says that 퓓₁ and 퓓₂ order acts the same way on corresponding decision problems.

I now show that GEU can represent a number of decision rules. Consider maximin with real-valued utilities (i.e., where the domain of maximin consists of all decision problems where the utility is real-valued). Let ED_max = (ℝ, {0,1}, ℝ, min, ), and let Pl_max be the plausibility measure such that Pl_max(U) is 0 if X = ∅ and 1 otherwise. For the decision problem described in Example 5.4.1,

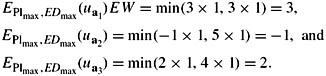
Note that E_{Pl_max}, ED_max(u_a) = worst_u(a_i), for i = 1, 2, 3. Of course, this is not a fluke. If DP = (DS, ℝ, u), where DS = (A, W, C), then it is easy to check that E_{Pl_max, ED_max}(u_a) = worst_u(a) for all actions a ∈ A (Exercise 5.39).

Take τ(DP) = (DS, ED_max, Pl_max, u). Clearly DP and τ(DP) are congruent; the agent's tastes have not changed. Moreover, it is immediate that GEU(τ(DP)) = maximin(DP). Thus, GEU represents maximin. (Although maximin is typically considered only for real-valued utility functions, it actually makes perfect sense as long as utilities are totally ordered. GEU also represents this "generalized" maximin, using essentially the same transformation τ ; see Exercise 5.40.)

Next, I show that GEU can represent minimax regret. For ease of exposition, I consider only decision problems DP = ((A, W, C), ℝ, u) with real-valued utilities such that M_DP = sup{u*(w) : w ∈ W} < ∞. (If M_DP =∞, given the restriction to simple acts, then it is not hard to show that every act has infinite regret; see Exercise 5.41.) Let ED_reg = ([0, 1], ℝ, ℝ, min, ⊗), where x ⊗ y = y − log(x) if x > 0, and x ⊗ y = 0 if x = 0. Note that ⊥= 0 and ⊤ = 1. Clearly, min is associative and commutative, and ⊤ ⊗ r = r − log(1) = r for all r ∊ ℝ. Thus, ED_reg is an expectation domain.

For ∅ ≠ U ⊆ W, define M_U = sup{u*(w) : w ∈ U}. Note that M_DP = M_W. Since, by assumption, M_DP < ∞, it follows that M_U < ∞ for all U ⊆ W. Let Pl_DP be the plausibility measure such that Pl_DP(∅) = 0 and Pl_M(U) = e^M_U−M_DP for U ≠ ∅.

For the decision problem described in Example 5.4.1, M_DP = 5. An easy computation shows that, for example,

Similar computations show that E_{Pl_DP, ED_reg}(u_{a_i}) = 5 − regret_u(a_i) for i = 1, 2, 3. More generally, it is easy to show that

for all acts a ∈ A (Exercise 5.42). Let τ be the decision-problem transformation such that τ(DP) = (DS, ED_reg, Pl_DP, u). Clearly, higher expected utility corresponds to lower regret, so GEU(τ(DP)) = regret(DP).

Note that, unlike maximin, the plausibility measure in the transformation from DP to τ(DP) for minimax regret depends on DP (more precisely, it depends on M_DP). This is unavoidable; see the notes for some discussion.

Finally, given a set of probability measures, consider the decision rules induced by and , (Formally, these rules take as inputs plausibilistic decision problems where the plausibility measure is Pl.) Proposition 5.4.3 shows that all these rules can be represented by GEU.

The following proposition summarizes the situation:

Proposition 5.4.3

GEU represents maximin, minimax regret, and the decision rules induced by and .

Conspicuously absent from the list in Proposition 5.4.3 is the decision rule determined by expected belief (i.e., a₁ ≽ a₂ iff E_Bel(u_a₁) ≥ E_Bel(u_a₂). In fact, this rule cannot be represented by GEU. To understand why, I give a complete characterization of the rules that can be represented.

There is a trivial condition that a decision rule must satisfy in order to be represented by GEU. Say that a decision rule 퓓 respects utility if the preference order on acts induced by 퓓 agrees with the utility ordering. More precisely, 퓓 respects utility if, given as input a decision problem DP with utility function u, if two acts a₁ and a₂ in DP induce constant utilities d₁ and d₂ (i.e., if u_{a_i} (w) = d_i for all w ∈ W, for i = 1, 2), then d₁ ≤ d₂ iff a₁ ≤_퓓(DP). It is easy to see that all the decision rules I have considered respect utility. In particular, it is easy to see that GEU respects utility, since the expected utility of the constant act with utility d is just d. (This depends on the assumption that ⊤ ⊗ d = d.) Thus, GEU cannot possibly represent a decision rule that does not respect utility. (Note that there is no requirement of respecting utility in Theorem 5.4.2, nor does there have to be. Theorem 5.4.2 starts with a preference order, so there is no utility function in the picture. Here, I am starting with a decision rule, so it makes sense to require that it respect utility.)

While respecting utility is a necessary condition for a decision rule to be representable by GEU, it is not sufficient. It is also necessary for the decision rule to treat acts that behave in similar ways similarly. Given a decision problem DP, two acts a₁, a₂ in DP are indistinguishable, denoted a₁ ~_DP a₂ iff either

DP is nonplausibilistic and u_a₁ = u_a₂, or
DP is plausibilistic, 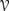(u_a₁) = 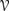(u_a₂), and Pl(u⁻¹ _a₁ (d)) = Pl(u⁻¹_a₂ (d)) for all utilities d in the common range of u_a₁ and u_a₂, where Pl is the plausibility measure in DP.

In the nonplausibilistic case, two acts are indistinguishable if they induce the same utility random variable; in the nonplausibilistic case, they are indistinguishable if they induce the same plausibilistic "utility lottery."

A decision rule is uniform if it respects indistinguishability. More formally, a decision rule 퓓 is uniform iff, for all DP in the domain of 퓓 and all a₁, a₂, a₃ in DP, if a₁ ~_DP a₂ then

Clearly GEU is uniform, so a decision rule that is not uniform cannot be represented by GEU. However, as the following result shows, this is the only condition other than respecting utility that a decision rule must satisfy in order to be represented by GEU:

Theorem 5.4.4

If 퓓 is a decision rule that respects utility, then 퓓 is uniform iff 퓓 can be represented by GEU.

Proof See Exercise 5.43.

Most of the decision rules I have discussed are uniform. However, the decision rule induced by expected belief is not, as the following example shows:

Example 5.4.5

Consider the decision problem where

A = {a₁, a₂};
W = {w₁, w₂, w₃};
C = {1, 2, 3};
u(j) = j, for j = 1, 2, 3;
a₁(w_j) = j and a₂(w_j) = 3 − j, for j = 1, 2, 3; and
Bel is the belief function such that Bel({w₁, w₂}) = Bel(W) = 1, and Bel(U) = 0 if U is not a superset of {w₁, w₂}.

Clearly a₁ ~_DP a₂, since u⁻¹_{a_i} (j) is a singleton, so Bel(u⁻¹_{a_i} (j)) = 0 for i = 1, 2 and j = 1, 2, 3. On the other hand, by definition,

while

It follows that the decision rule that orders acts based on their expected belief is not uniform, and so cannot be represented by GEU.

The alert reader may have noticed an incongruity here. By Theorem 2.4.1, Bel = (_Bel)_* and, by definition, E_Bel = E_{_Bel}. Moreover, the preference order induced by E_{_Bel} can be represented by GEU. There is no contradiction to Theorem 5.4.4 here. If 퓓_BEL is the decision rule induced by expected belief and DP is the decision problem in Example 5.4.5, then there is no decision problem τ(DP) = (DS, ED′, Bel, u) such that GEU (τ(DP)) = 퓓_BEL(DP). Nevertheless, GEU ((A, W, C), ED_D, Pl_{_Bel}, u) = 퓓_BEL(DP). (Recall that ED_D is defined at the end of Section 5.4.2.) (A, W, C), ED_D, Pl_{_Bel}, u) and DP are not congruent; Pl_{_Bel} and Bel are not identical representations of the agent's beliefs. They are related, of course. It is not hard to show that if Pl_{_Bel} (U) ≤ Pl_{_Bel} (V, then Bel(U) ≤ Bel(V), although the converse does not hold in general (Exercise 5.44).

For a decision rule 퓓₁ to represent a decision rule 퓓₂, there must be a decision-problem transformation τ such that τ(DP) and DP are congruent and 퓓₂(τ(DP)) = 퓓₂(DP) for every decision problem DP in the domain of 퓓₂. Since τ(DP) and DP are congruent, they agree on the tastes and (if they are both plausibilistic) the beliefs of the agent. I now want to weaken this requirement somewhat, and consider transformations that preserve an important aspect of an agent's tastes and beliefs, while not requiring them to stay the same.

There is a long-standing debate in the decision-theory literature as to whether preferences should be taken to be ordinal or cardinal. If they are ordinal, then all that matters is their order. If they are cardinal, then it should be meaningful to talk about the differences between preferences, that is, how much more an agent prefers one outcome to another. Similarly, if expressions of likelihood are taken to be ordinal, then all that matters is whether one event is more likely than another.

Two utility functions u₁ and u₂ represent the same ordinal tastes if they are defined on the same set C of consequences and for all c₁, c₂ ∈ C, u₁(c₁) ≤ u₁(c₂) iff u₂(c₁) ≤ u₂(c₂). Similarly, two plausibility measures Pl₁ and Pl₂ represent the same ordinal beliefs if Pl₁ and Pl₂ are defined on the same domain W and Pl₁(U) ≤ Pl₁(V) iff Pl₂(U) ≤ Pl₂(V) for all U, V ⊆ W. Finally, two decision problems DP₁ and DP₂ are similar iff they involve the same decision situations, their utility functions represent the same ordinal tastes, and their plausibility measures represent the same ordinal beliefs. Note that two congruent decision problems are similar, but the converse may not be true.

Decision rule 퓓₁ ordinally represents decision rule 퓓₂ iff there exists a decision-problem transformation τ such that, for all decision problems DP in the domain of 퓓₂, the decision problem τ(DP) is in the domain of 퓓₁, DP is similar to τ(DP), and 퓓₁(τ(DP)) = 퓓₂(DP). Thus, the definition of emulation is just like that of representation, except that τ(DP) is now required only to be similar to DP, not congruent.

I now want to show that GEU can ordinally represent essentially all decision rules. Doing so involves one more subtlety. Up to now, I have assumed that the range of a plausibility measure is partially ordered. To get the result, I need to allow it to be partially preordered. That allows two sets that have equivalent plausibility to act differently when combined using ⊕ and ⊗ in the computation of expected utility. So, for this result, I assume that the relation ≤ on the range of a plausibility measure is reflexive and transitive, but not necessarily antisymmetric. With this assumption, GEU ordinally represents 퓓_BEL (Exericse 5.45). In fact, an even more general result holds.

Theorem 5.4.6

If 퓓 is a decision rule that respects utility, then GEU ordinally represents 퓓.

Proof See Exercise 5.46.

Theorem 5.4.6 shows that GEU ordinally represents essentially all decision rules. Thus, there is a sense in which GEU can be viewed as a universal decision rule.

Thinking of decision rules as instances of expected utility maximization gives a new perspective on them. The relationship between various properties of an expectation domain and properties of decision rules can then be studied. To date, there has been no work on this topic, but it seems like a promising line of inquiry.