5.3 Plausibilistic Expectation

My goal in this section is to define a general notion of expectation for plausibility measures that generalizes the notions that have been considered for other representations of uncertainty. Since expectation is defined in terms of operations such as + and , expecstation for plausibility is more interesting if there are analogues to + and , much as in the case of algebraic conditional plausibility spaces. In general, the analogues of + and used for expectation may be different from that used for plausibility; nevertheless, I still denote them using ⊕ and ⊗.

How can expectation for a random variable X on W be defined? To start with, a plausibility measure on W is needed. Suppose that the range of the plausibility measure is D₁ and the range of the random variable X is D₂.(D₂ may not be the reals, so X is not necessarily a gamble.) To define an analogue of (5.2), what is needed is an operation ⊗ that maps D₁ D₂ to some valuation domain D₃, where D₃ extends D₂, and an operation ⊕ that maps D₃ D₃ to D₃. If d₂ is a prize, as in the example at the beginning of the chapter, then d₁ ⊗ d₂ can be viewed as the "value" of getting d₂ with likelihood d₁. Similarly, d₃ ⊕ d₄ can be viewed as the value of getting both d₃ and d₄. It is often the case that D₂ = D₃, but it is occasionally convenient to distinguish between them.

Definition 5.3.1

An expectation domain is a tuple ED = (D₁, D₂, D₃, ⊕, ⊗), where

D₁ is a set partially ordered by ≤₁;
D₂ and D₃ are sets partially preordered by ≤₂ and ≤₃, respectively;
there exist elements ⊥ and ⊤ in D₁ such that ⊥≤₁ d ≤₁ ⊤ for all d ∈ D₁;
D₂ ⊆ D₃ and ≤₂ is the restriction of ≤₃ to D₂;
⊕ : D₃ D₃ → D₃;
⊗ : D₁ D₂ → D₃;
⊕ is commutative and associative;
⊤⊗ d₂ = d₂.

The standard expectation domain is ([0, 1] ℝ, ℝ, +, ), where ≤₁, ≤₂, and ≤₃ are all the standard order on the reals. The standard expectation domain is denoted ℝ.

Given an expectation domain ED = (D₁, D₂, D₃, ⊕, ⊗), a plausibility measure Pl with range D₁, and a random variable X with range D₂, one notion of expected value of X with respect to Pl and ED, denoted E_{Pl, ED}(X), can be defined by obvious analogy to (5.2):

(I include ED in the subscript because the definition depends on ⊕ and ⊗; I omit ED if ⊗ and ⊕ are clear from context.)

It is also possible to define an analogue of (5.3) if D₂ is linearly ordered and a notion of subtraction can be defined in ED; I don't pursue this further here and focus on (5.14) instead.

It is almost immediate from their definitions that E_μ, E_κ, E′_Poss (as defined in Exercise 5.30), and E″_Poss (as defined in Exercise 5.31) can be viewed as instances of E_{Pl, ED}, for the appropriate choice of ED. It is not hard to see that E_Pl is also an instance of E_Pl,SD. Since the construction will be useful in other contexts, I go through the steps here. Suppose that the probability measures in are indexed by I. Let ED_D, where

D₁ = D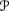, the functions from to [0, 1] with the pointwise ordering (recall that this is just the range of Pl);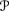
D₂ consists of the constant functions from 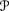to ℝ;
D₃ consists of all functions from 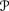to ℝ, again with the pointwise ordering;
⊕ is pointwise addition;
and ⊗ is pointwise multiplication.

Since the constant function can be identified with the real number b, it follows that D₂ can be identified with ℝ. It is easy to see that E_{Pl,ED_D} (Exercise 5.33).

Although E and E cannot be directly expressed using E_{Pl, ED}, the order they induce on random variables can be represented. Consider E. Let ED′_D be identical to ED_D except that the order on D₃ is modified so that, instead of using the pointwise ordering, f ≤ g iff inf_μ∊ f(μ) ≤ inf_μ∊ g(μ). (Note that this is actually a preorder.) It is almost immediate from the definitions that E_{Pl,ED′_D} (X) ≤ E_Pl,ED′ (Y) iff E(x) ≤ E(Y). Similarly, the order induced by can be represented by simply changing the order on D₃ so that it uses sup rather than inf. Since E_Bel = E_{_Bel}, it follows that the order on random variables induced by E_Bel can also be represented. As discussed in the next section, what often matters in decision making is the order that expectation induces on random variables so, in a sense, this is good enough.

Note that E_Pl() = b. Properties like subadditivity, superadditivity, monotonicity, or positive affine homogeneity make sense for E_Pl. Whether they hold depends in part on the properties of ⊕, ⊗, and Pl; I do not pursue this here (but see Exercise 5.34). Rather, I consider one of the most important applications of expectation, decision making, and see to what extent plausibilistic expectation can help in understanding various approaches to making decisions.