3.10 Jeffrey s Rule
|
3.10 Jeffrey's Rule
Up to now, I have assumed that the information received is of the form "the actual world is in U." But information does not always come in such nice packages.
Example 3.10.1
Suppose that an object is either red, blue, green, or yellow. An agent initially ascribes probability 1/5 to each of red, blue, and green, and probability 2/5 to yellow. Then the agent gets a quick glimpse of the object in a dimly lit room. As a result of this glimpse, he believes that the object is probably a darker color, although he is not sure. He thus ascribes probability .7 to it being green or blue and probability .3 to it being red or yellow. How should he update his initial probability measure based on this observation?
Note that if the agent had definitely observed that the object was either blue or green, he would update his belief by conditioning on {blue, green}. If the agent had definitely observed that the object was either red or yellow, he would condition on {red, yellow}. However, the agent's observation was not good enough to confirm that the object was definitely blue or green, nor that it was red or yellow. Rather, it can be represented as .7{blue, green};.3{red, yellow}. This suggests that an appropriate way of updating the agent's initial probability measure μ is to consider the linear combination μ′ = .7μ|{blue, green}+ .3μ|{red, yellow}. As expected, μ′({blue, green}) = .7 and μ′({red, yellow}) = .3. Moreover, μ′(red) = .1, μ′(yellow) = .2, and μ′(blue) = μ′(green) = .35. Thus, μ′ gives the two sets about which the agent has information— {blue, green} and {red, yellow}—the expected probabilities. Within each of these sets, the relative probability of the outcomes remains the same as before conditioning.
More generally, suppose that U1, …, Un is a partition of W (i.e., ∪i=1nUi = W and Ui ∩ Uj = ∅ for i ≠ j) and the agent observes α1U1;…; αnUn, where α1 + … + αn = 1. This is to be interpreted as an observation that leads the agent to believe Uj with probability αj, for j = 1, …, n. In Example 3.10.1, the partition consists of two sets U1 = {blue, green} and U2 = {red, yellow}, with α1 = .7 and α2 = .3. How should the agent update his beliefs, given this observation? It certainly seems reasonable that after making this observation, Uj should get probability αj, j = 1, …, n. Moreover, since the observation does not give any extra information regarding subsets of Uj, the relative likelihood of worlds in Uj should remain unchanged. This suggests that μ | (α1U1;…; αnUn), the probability measure resulting from the update, should have the following property for j = 1, …, n :
![]()
Taking V = Uj in J, it follows that
![]()
Moreover, if αj > 0, the following analogue of (3.2) is a consequence of J (and J1):
![]()
(Exercise 3.39).
Property J uniquely determines what is known as Jeffrey's Rule of conditioning (since it was defined by Richard Jeffrey). Define
![]()
(I take αj μ(V | Uj) to be 0 here if αj = 0, even if μ(Uj) = 0.) Jeffrey's Rule is defined as long as the observation is consistent with the initial probability (Exercise 3.40); formally this means that if αj > 0 then μ(Uj) > 0. Intuitively, an observation is consistent if it does not give positive probability to a set that was initially thought to have probability 0. Moreover, if the observation is consistent, then Jeffrey's Rule gives the unique probability measure satisfying property J (Exercise 3.40).
Note that μ|U = μ|(1U;0U), so the usual notion of probabilistic conditioning is just a special case of Jeffrey's Rule. However, probabilistic conditioning has one attractive feature that is not maintained in the more general setting of Jeffrey's Rule. Suppose that the agent makes two observations, U1 and U2. It is easy to see that if μ(U1 ∩ U2) ≠ 0, then
![]()
(Exercise 3.41). That is, the following three procedures give the same result: (a) condition on U1 and then U2, (b) condition on U2 and then U1, and (c) condition on U1 ∩ U2 (which can be viewed as conditioning simultaneously on U1 and U2). The analogous result does not hold for Jeffrey's Rule. For example, suppose that the agent in Example 3.10.1 starts with some measure μ, observes O1 = .7{blue, green}; .3{red, yellow}, and then observes O2 = .3{blue, green}; .7{red, yellow}. Clearly, (μ|O1)|O2 ≠ (μ|O2)|O1. For example, (μ|O1)|O2 ({blue, green}) = .3, while (μ | O2)|O1({blue, green}) = .7. The definition of Jeffrey's Rule guarantees that the last observation determines the probability of {blue, green}, so the order of observation matters. This is quite different from Dempster's Rule, which is commutative. The importance of commutativity, of course, depends on the application.
There are straightforward analogues of Jeffrey's Rule for sets of probabilities, belief functions, possibility measures, and ranking functions.
-
For sets of probabilities, Jeffrey's Rule can just be applied to each element of the set (throwing out those elements to which it cannot be applied). It is then possible to take upper and lower probabilities of the resulting set. Alternatively, an analogue to the construction of Pl
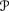 can be applied.
can be applied. -
For belief functions, there is an obvious analogue of Jeffrey's Rule such that
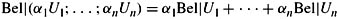
(and similarly with | replaced by ||). It is easy to check that this in fact is a belief function (provided that Plaus(Uj) > 0 if αj > 0, and αj Bel|Uj is taken to be 0 if αj = 0, just as in the case of probabilities). It is also possible to apply Dempster's Rule in this context, but this would in general give a different answer (Exercise 3.42).
-
For possibility measures, the analogue is based on the observation that + and for probability becomes max and min for possibility. Thus, for an observation of the form α1U1;…; αnUn, where αi ∈ [0, 1] for i = 1, …, n and max(α1, …, αn) = 1,
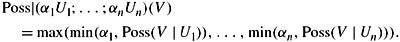
-
For ranking functions, + becomes min and the role of 1 is played by 0. Thus, for an observation of the form α1U1;…; αnUn, where αi ∊ ℕ*, i = 1,…,n and min(α1, …, αn) = 0,
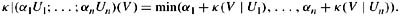
|
EAN: 2147483647
Pages: 140
- Chapter III Two Models of Online Patronage: Why Do Consumers Shop on the Internet?
- Chapter IV How Consumers Think About Interactive Aspects of Web Advertising
- Chapter V Consumer Complaint Behavior in the Online Environment
- Chapter X Converting Browsers to Buyers: Key Considerations in Designing Business-to-Consumer Web Sites
- Chapter XVI Turning Web Surfers into Loyal Customers: Cognitive Lock-In Through Interface Design and Web Site Usability