3.9 Conditioning Plausibility Measures

How should conditioning be defined in the case of plausibility measures? Proceeding in a manner similar in spirit to that for probability, define a conditional plausibility space (cps) to be a tuple (W, , ′, Pl), where ′ is a Popper algebra over W, Pl: ′ → D, D is a partially ordered set of plausibility values, and Pl is a conditional plausibility measure (cpm) that satisfies the following conditions:

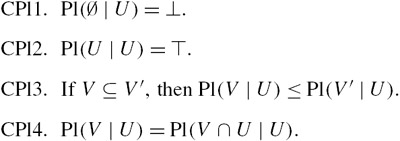
CPl1–3 just say that Pl1–3 hold for Pl( | U), so that Pl( | U) is a plausibility measure for each fixed U ∊ ′. CPl4 is the obvious analogue of CP4 . Since there is no notion of multiplication (yet!) for plausibility measures, it is not possible to give an analogue of CP3 for conditional plausibility.

(W, , ′, Pl) is acceptable if U ∊ ′ and Pl(V | U) ≠⊥ implies that V ∩ U ∊ ′. Acceptability is a generalization of the observation that if μ(V) ≠ 0, then conditioning on V should be defined. It says that if Pl(V | U) ≠⊥, then conditioning on V ∩ U should be defined. All the constructions that were used for defining conditional likelihood measures result in acceptable cps's. On the other hand, acceptability is not required in the definition of conditional probability space (Definition 3.2.3).

CPl1–4 are rather minimal requirements. Should there be others? The following coherence condition, which relates conditioning on two different sets, seems quite natural:

It can be shown that CPl5 implies CPl4 if ′ has the property that characterizes acceptable cps's—that is, if U ∊ ′ and Pl(V | U) > ⊥, then V ∩ U ∊ ′ (Exercise 3.26). While CPl5 seems quite natural, and it holds for all conditional probability measures, conditional possibility measures constructed as in Section 3.7 from unconditional possibility measures (both Poss( | U) and Poss( || U)), and conditional ranking functions as constructed in Section 3.8 from unconditional ranking functions, it does not hold in general for _*(.|U), Bel(.|U), or Bel( || U) (Exercise 3.27). For example, in the case of _*, the problem is that just because μ ∊ gives the minimum value for μ(U ∩ V) does not mean it also gives the minimum value for μ(V | U). The minimization operation does not "commute" with conditioning. Without this commutativity, the "natural" coherence condition CPl5 no longer holds.

3.9.1 Constructing Conditional Plausibility Measures

Given an unconditional plausibility measure Pl, is it possible to construct a conditional plausibility measure extending Pl? It turns out that there is. Perhaps the easiest way of understanding it is to consider first the problem of getting a conditional plausibility measure extending the representation Pl of a set of probability measures.

Assume that all the probability measures in are defined on some algebra over W. Recall that in the unconditional case, the domain of Pl is also and its range is D, the set of functions from to [0, 1]. In particular, Pl(U)(μ) = μ(U), for U ∊ . The plan now is to define Pl(V|U) to be that function f_V|U from to values in [0, 1] such that Pl (V | U)(μ) = μ = μ(V | U). The only question is what the domain of Pl ought to be; that is, on what Popper algebra ′ should Pl be defined? This issue also arose in the context of defining _*(V | U). One approach would be to take ′ to consist of all U ∊ such that μ(U) > 0 for all μ ∊ . This would result in a cps that, in general, is not acceptable (Exercise 3.28). As in the case of _*, conditioning would not be defined for many cases of interest. Instead (again, just as in the case of _*), I take ′ to consist of all V such that μ(V) > 0 for some μ ∊ . But then what should f_V|U (μ) be if μ(U) = 0? To deal with this, I add a value "undefined," denoted ⋆, to the domain.

Formally, extend D by allowing functions that have value ⋆. More precisely, let D′ consist of all functions f from to [0, 1] ∪ {⋆} such that f (μ) ≠⋆ for at least one μ ∊ . The idea is to define Pl(V | U) = f_V|U, where f_V|U (μ) = μ(V | U) if μ(U) > 0 and ⋆ otherwise. (Note that this agrees with the previous definition, which applies only to the case where μ(U) > 0 for all μ ∊ .) There is a problem though. CPl1 says that f_∅|U must be ⊥ for all U. Thus, it must be the case that f_∅|U₁ = f_∅|U₂ for all U₁, U₂ ⊆ W. But if μ∊ and U₁, U₂ ⊆ W are such that μ(U₁)> 0 and μ(U₂) = 0, then f_∅|U₁(μ) = 0 and f_∅|U₂(μ) =⋆, so f_∅|U₁ ≠ f_∅|U₂. A similar problem arises with CPl2.

To deal with this problem, D′ must be slightly modified. Say that F ∊ D′ is equivalent to ⊥_D* if f (μ) is either 0 or * for all μ ∊ ; similarly, f is equivalent to ⊺_D* if f(μ) is either 1 or * for all μ ∊ . (Since, by definition of D′, f(μ) ≠ * for at least one μ ∊ , an element in D′ cannot be equivalent to both ⊺_D* and ⊥_D*.) Let D*. be the same as D′ except that all elements equivalent to ⊥_D* are identified (and viewed as one element) and all elements equivalent to ⊺_D* are identified. More precisely, let D* = {⊥_D*, ⊺_D*} ∩ {f ∊ D′: f is not equivalent to ⊺_D* or ⊥_D*}. Define the order ≤_D* on D* by taking f ≤_D* if one of the following three conditions holds:

f = ⊥_D*
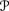
g = ⊥_D*
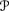
neither f nor g is ⊥_D* 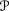or ⊥_D* 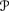and, for all μ ∊ 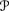, either f (μ) = g(μ) = ⋆ or f (μ) ≠⋆, g(μ) ≠⋆, and f (μ) ≤ g(μ).

Now define

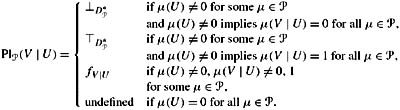
It is easy to check that this construction results in an acceptable cps that satisfies CPl5 and is an extension of Pl (Exercise 3.29).

This construction can be used, with essentially no change, if is a set of arbitrary plausibility measures; in that case, it gives a single cpm that represents . More interestingly, a similar construction can be used to construct a conditional plausibility measure from an arbitrary unconditional plausibility measure Pl defined on an algebra . The idea is quite straightforward. Given an unconditional plausibility measure Pl with range D, for each set U ∊ , start by defining a new plausibility measure Pl_U with range D_U = {d ∈ D : d ≤ Pl(U)} by taking Pl_U(V) = Pl(V ∩ U). Note that ⊤_{D_U} = Pl(U). Thus, defining Pl(V | U) as Pl_U(V) will not quite work, because then CPl2 is not satisfied; in general, Pl_U (W) ≠ Pl_V (W).

To get a cps, let D′ = {(d, V) : V ⊆ W, d ≤ Pl(V), Pl(V) > ⊥_D}. Say that (d, V) is equivalent to ⊥_D* if d = ⊥_D; say that (d, V) is equivalent to ⊤_D* if d = Pl(V). Now let D* = {⊥_D*, ⊤_D*}∪{(d, V) ∈ D′ : (d, V) is not equivalent to ⊤_D* or ⊥_D*}. Then define d ≤_D* d′ for d, d′ ∈ D* iff d = ⊥_D*, d′ = ⊤_D*, or there is some V ⊆ W such that d = (d₁, V), d′ = (d₂, V), and d₁ ≤_D d₂. Finally, for U, V ∊ , define

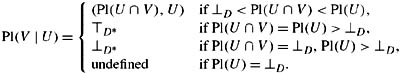
I leave it to the reader to check that this gives an acceptable cps that satisfies CPl5 and is an extension of Pl, if d ∈ D is identified with (d, W) ∈ D* (Exercise 3.30). It is important that Pl(V | U) is undefined if Pl(U) = ⊥_D; if Pl(V | U) were instead defined as ⊥_D*, then ⊤_D* would be equal to ⊥_D*, and the whole construction would trivialize. In particular, the resulting cpm would not extend Pl.

3.9.2 Algebraic Conditional Plausibility Spaces

The definitions of conditional possibility and conditional ranking were motivated in part by considering analogues for possibility and ranking of addition and multiplication in probability. We saw in Section 2.8 that an analogue ⊕ of addition could be added to plausibility. Yet more structure emerges if, in addition, there is an analogue to multiplication.

Definition 3.9.1

A cps (W, , ′, Pl) where Pl has range D is algebraic if it is acceptable and there are functions ⊕ and ⊗ mapping D D to D such that the following conditions hold:

Alg1. Pl is additive with respect to ⊕; that is, Pl(V ∪ V′ | U) = Pl(V | U) ⊕ Pl(V′ | U) if V, V′ ∊ 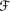are disjoint and U ∊ ′.
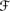Alg2. PI(U₁ ∩ U₂ | U₃) = PI(U₁ | U₂ ∩U₃) ⊗ PI(U₂ | U₃) if U₂ ∩ U₃ ∊ 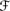′, U₁, U₂, U₃ ∊ .
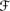Alg3. ⊗ distributes over ⊕; more precisely, a ⊗ (b₁ ⊕ … ⊕ b_n) = (a ⊗ b₁) ⊕ … ⊕ (a ⊗ b_n) if (a, b₁), …, (a, b_n), (a, b₁ ⊕ … ⊕ b_n) ∈ Dom(⊗) and (b₁, …, b_n), (a ⊗ b₁, …, a ⊗ b_n) ∈ Dom(⊕), where Dom ⊕ = {(Pl(V₁ | U),…, Pl(V>_n|U)) : V₁,…, V_n ∊ 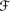} are pairwise disjoint and U ∊ 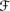′ and Dom ⊗ = {(Pl(U₁|U₂ ∩ U₃), Pl(U₂|U₃)) : U₂ ∩ U₃ ∊ F′, U₁, U₂, U₃ ∊ 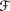}. (The reason that this property is required only for tuples in Dom(⊕) and Dom(⊗) is discussed shortly. Note that parentheses are not required in the expression b₁ ⊕ … ⊕ b_n although, in general, ⊕ need not be associative. This is because it follows immediately from Alg1 that ⊕ is associative and commutative on tuples in Dom(⊕).)

Alg4. If (a, c), (b, c) ∈ Dom(⊗), a ⊗ c ≤ b ⊗ c, and c ≠ ⊥, then a ≤ b.

If (W, , ′ Pl) is an algebraic cps, then Pl is called an algebraic cpm.

Alg1 and Alg2 are clearly analogues of CP2 and CP3. The restrictions in Alg3 and Alg4 to tuples in Dom(⊕) and Dom(⊗) make these conditions a little more awkward to state. It may seem more natural to consider a stronger version of, say, Alg4 that applies to all pairs in D D, such as

Alg4′. if a ⊗ c = b ⊗ c and ≠ ⊥, then a = b.

However, as Proposition 3.9.2 shows, by requiring that Alg3 and Alg4 hold only for tuples in Dom(⊕) and Dom(⊗) rather than on all tuples in D D, some cps's of interest become algebraic that would otherwise not be. Since ⊕ and ⊗ are significant mainly to the extent that Alg1 and Alg2 hold, and Alg1 and Alg2 apply to tuples in Dom(⊕) and Dom(⊗), respectively, it does not seem unreasonable that properties like Alg3 and Alg4 be required to hold only for these tuples.

Proposition 3.9.2

The constructions for extending an unconditional probability measure, ranking function, possibility measure (using either Poss( |U) or Poss( ||U)), and the plausibility measure Pl defined by a set of probability measures to a cps result in algebraic cps's.

Proof It is easy to see that in each case the cps is acceptable. It is also easy to find appropriate notions of ⊗ and ⊕ in the case of probability measures, ranking functions, and possibility measures using Poss(V | U). For probability, clearly ⊕ and ⊗ are essentially + and ; however, since the range of probability is [0, 1], a ⊕ b must be defined as max(1, a + b), and Alg3 holds only for Dom(⊕) = {(a₁, …, a_k) : a₁ + … + a_k ≤ 1}. For ranking, ⊕ and ⊗ are min and +; there are no constraints on Dom(⊕) and Dom(⊗). For Poss(V ||U), ⊕ is max and ⊗ is ; again, there are no constraints on Dom(max) and Dom( ). I leave it to the reader to check that Alg1–4 hold in all these cases (Exercise 3.31).

For Poss(V | U), ⊕ is again max and ⊗ is min. There are no constraints on Dom(max); however, note that (a, b) ∈ Dom(min) iff either a < b or a = 1. For suppose that (a, b) = (Pl(U₁|U₂ ∩ U₃), Pl(U₂|U₃)), where U₂ ∩ U₃ ∊ ′, U₁, U₂, U₃ ∊ . If Poss(U₁ ∩ U₂ ∩ U₃) = Poss(U₂ ∩ U₃) then a = Poss(U₁ ∩ U₂|U₃) = 1; otherwise, Poss(U₁ ∩ U₂ ∩ U₃) < Poss(U₂ ∩ U₃), in which case a = Poss(U₁ ∩ U₂ ∩ U₃) < Poss(U₂ ∩ U₃) ≤ Poss(U₂|U₃) = b. It is easy to check that Alg1–3 hold (Exercise 3.32). While min does not satisfy Alg4′—certainly min(a, c) = min(b, c) does not in general imply that a = b—Alg4 does hold. For if min(a, c) = min(b, c) and a = 1, then clearly b = 1. On the other hand, if a < c, then min(a, c) = a and the only way that a = min(b, c), given that b < c or b = 1, is if a = b.

Finally, for Pl and ⊗ are essentially pointwise addition and multiplication. But there are a few subtleties. As in the case of probability, Dom(⊕) essentially consists of sequences that sum to at most 1 for each index i. However, care must be taken in dealing with ⊥_D* and ⊺_D*. To be precise, Dom(⊕) consists of all tuples (f₁, …, f_n) such that either

For all j, k ∈{1, …, n} and μ ∊
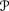
1. f_j ≠ ⊺_D*;
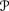2. if f_j, f_k ≠ ⊥_D*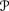, then f_j(μ) = ⋆ iff f_k(μ) = ⋆; and
3. ∑_{{h:f_h ≠ ⊥_D*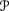, f_h(μ)≠*}} f_h(μ) ≤ 1;
or
there exists j such that f_j = ⊺_D* 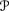and f_k = ⊥_D* for all k ≠ j.

Dom(⊗) consists of pairs (f, g) such that either (a) one of f or g is in {⊥_D*, ⊥_D*} or (b) neither f nor g is in {⊥_D*, ⊥_D*} and g(μ) ∈{0, ⋆} iff f (μ) = ⋆.

The definition of ⊕ is relatively straightforward. Define f ⊕ ⊺_D* = ⊺_D* ⊕ f = ⊺_D* and f ⊕ ⊥_D* = ⊥_D* ⊕ f = f. If {f, g} ∩ {⊥_D*, ⊺_D*} = , then f ⊕ g = h, where h(μ) = min(1, f (μ) + g(μ)) (taking a +⋆= ⋆+ a = ⋆ and min(1, ⋆) = ⋆). In a similar spirit, define f ⊗ ⊺_D* = ⊺_D* ⊗ f = f and f ⊗ ⊥_D* = ⊥_D* ⊗ f = ⊥_D*; if {f, g} ∩ {⊥_D*, ⊺_D*} = , then f ⊗ g = h, where h(μ) = f (μ) g(μ) (taking ⋆ a = a ⋆ = ⋆ if a ≠ 0 and ⋆ 0 = 0 ⋆ = 0). It is important that ⋆ 0 = 0 and ⋆ ⋆ = ⋆, since otherwise Alg3 may not hold. For example, suppose = {μ₁, μ₂, μ₃} and a function f ∊ D′ is identified with the tuple (f (μ₁, f(μ₂), f(μ₃)). Then, according to Alg3, ((1/2, ⋆, 1/2) ⊗ (a, 0, b)) ⊕ ((1/2, ⋆, 1/2)) ⊗ (a, 0, b)) = ((1/2, ⋆, 1/2) ⊕ (1/2, ⋆, 1/2)) ⊗ (a, 0, b) = (a, 0, b) (since (1/2, * 1/2) ⊕ (1/2, *, 1/2) = ⊺_D*) and, similarly, ((1/2, ⋆, 1/2) ⊗ (a, ⋆, b)) ⊕ ((1/2, ⋆, 1/2)) ⊗ (a, ⋆, b)) = (a, ⋆, b). Since ⋆ 0 = 0 and ⋆ ⋆ = ⋆, these equalities hold. I leave it to the reader to check that, with these definitions, Alg1–4 hold (Exercise 3.33).

As observed in Section 2.8, there is no analogue to ⊕ for belief functions and lower probabilities. Thus, these representations of uncertainty are not algebraic.

Many of the properties that are associated with (conditional) probability hold more generally for algebraic cps's. I consider three of them here that will prove useful in Section 4.5. The first two say that ⊥ and ⊤ act like 0 and 1 with respect to addition and multiplication. Let Range(Pl) = {d :Pl(V | U) = d for some (V, U) ∊ ′.

Lemma 3.9.3

If (W, , ′, P1) is an algebraic cps, then d ⊕⊥ = ⊥⊕ d = d for all d ∈ Range(Pl).

Proof See Exercise 3.34.

Lemma 3.9.4

If (W, , ′, Pl) is an algebraic cps then, for all d ∈ Range(Pl),

d ⊗⊤ = d;
if d ≠ ⊥, then ⊤⊗ d = d;
if d ≠ ⊥, then ⊥⊗ d = ⊥;
if (d, ⊥) ∈ Dom(⊗), then ⊤⊗⊥ = d ⊗⊥ = ⊥⊗⊥ = ⊥.

Proof See Exercise 3.35.

The third property is an analogue of a standard property for probability that shows how Pl(V | U) can be computed by partitioning it into subsets.

Lemma 3.9.5

Suppose that (W, , ′, Pl) is an algebraic cps, A₁, …, A_n is a partition of W, A₁,…, A_n ∊ , and U ∊ ′. Then

Proof See Exercise 3.36.

Notice that if A_i ∩ U ∊ ′, then Pl(V |A_i ∩ U) ⊗ Pl(A_i|U) = Pl(V ∩ A_i|U) by Alg2. Thus, the terms arising on the right-hand side of the equation in Lemma 3.9.5 are in Dom(⊕). As I observed earlier, this means that there is no need to put in parentheses; ⊕ is associative on terms in Dom(⊕).

I conclude this section by abstracting a property that holds for all the constructions of cps's from unconditional plausibility measures (i.e., the constructions given in the case of Poss, ranking functions, probability, Pl, and plausibility). A cps (W, , ′, Pl) is standard if ′ = {U: Pl(U) ≠ ⊺}. Note that all the constructions of cps's from unconditional plausibility measures that have been considered result in standard cps's. This follows from a more general observation. (W, , ′, Pl) is determined by unconditional plausibility if there is a function g such that Pl(V | U) = g(Pl(V ∩ U|W), Pl(U|W)) for all (V, U) ∊ ′. It is almost immediate from the definitions that all the constructions of cps's constructed from unconditional plausibilities result in cps's that are determined by unconditional plausibility. If an acceptable cps is determined by unconditional plausibility, then it must be standard.

Lemma 3.9.6

If (W, , ′, Pl) is an acceptable cps determined by unconditional plausibility such that Pl(W) ≠ Pl(∅), then (W, , ′, Pl) is a standard cps.

Proof See Exercise 3.38.