The Legend of the Maze of the Minotaur

About 4,000 years ago, the wealthy seafaring Minoans built many wonderful structures on the island of Crete. These structures included lovely stone-walled palaces, probably the first stone paved road in the world, and, reputedly, a huge stone labyrinth on a seaside cliff called The Maze of the Minotaur.

The Minotaur of Greek mythology was a monster with the head of a bull and the body of a man, borne by Pasiphaë, Queen of Crete, and sired by a snow-white bull. According to legend, the god Poseidon who sent the white bull to Minos, King of Crete, was so angered by Minos' refusal to sacrifice the bull that Poseidon forced the union of Queen Pasiphaë and the beast. Thus the monster Minotaur was born. King Minos ordered construction of the great labyrinth as the Minotaur's prison. The beast was confined in the maze and fed human sacrifices, usually young Greeks, in annual rituals at which young men and women performed gymnastics on the horns of bulls and some unfortunate persons were dropped through a hole into the labyrinth's tunnels. The sacrifices continued until a Greek Hero named Theseus killed the Minotaur.

The Minoans did give their sacrifices a sporting chance. Reportedly, there was another exit besides the hole that the sacrifices were dropped through to enter the maze. If the sacrificial person was able to find the exit before the Minotaur found them, then they were free.

It was rumored that a bright physician from Egypt traversed the maze and escaped. The Egyptian succeeded by placing one hand on the wall and keeping it there until he came upon an exit. This technique kept him from becoming lost and wandering in circles.

The Egyptian's technique-always branching the same direction-is called an algorithm. An algorithm is any special method of solving a certain kind of problem. This algorithm does not guarantee that the path followed will be the shortest path between the entrance and exit. The length of the path traversed could be quite long, depending on where the exit is relative to the entrance. Note in Figure 11.1, which shows a maze with an exit, that the right-hand path, marked by the dotted line, is significantly shorter than the left-hand path, marked with the dashed line.

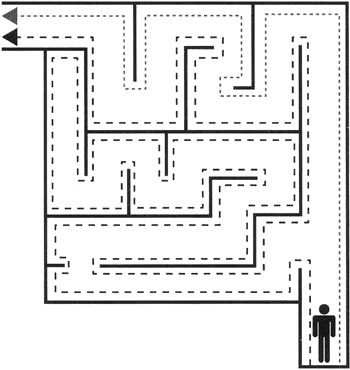
Figure 11.1: Maze with an exit.

The technique used by the fabled Egyptian will only work if the maze structure has certain characteristics, namely:

• There cannot be any pits or traps to fall into along the way. (No Minotaur can block the way.)

• The exit must be along a wall where it can be detected in the dark by a hand.

• The hole in the roof will not be found unless some landmark is erected on the spot.

• The exit must be along a wall that is connected to other maze walls, meaning that it is not on an island, as shown in Figure 11.2.

  
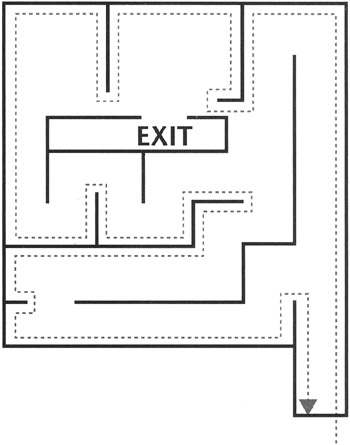
  Figure 11.2: Maze with island exit. The entrance to this maze cannot be used as an exit.

If the maze conforms to these rules and if one sure path is all that's required, then the Egyptian's algorithm will always work. This technique is systematic and reproducible. It does not matter which hand you use as long as you do not change hands after you start. This is the simplest maze problem and possibly the most fundamental general technique for finding a solution.

If the maze has no exit, the Egyptian's algorithm would eventually lead him back to the entrance. In a no-exit maze, the left-hand and right-hand paths are the same length; one is simply the reverse of the other.

Undoubtedly, there are nitpickers in the readership saying, "Ahh, but the entrance is also an exit." Under some circumstances, the entrance could be a viable exit, given the proper tools. Say, for instance, the person inside the maze had an accomplice on the outside who was willing to provide him with a rope or a ladder, as Theseus did (more on him in a minute). It is worth mentioning the case where a person is dropped into an enormous maze and the first wall that comes to hand is part of an island with no exit on it. If this person uses only the one-hand-on-the-wall method, she will probably never find an exit. If this person marked her starting point, she would eventually determine that there was no available exit and would probably try a different method, such as wandering away from the island.

Trying to find a path to the exit by wandering through the maze does have a chance of success. In fact, wandering the maze actually has a better chance of finding an island exit than the one-hand-on-the-wall method.

Trying to find a path through a maze by wandering through it, without a method, is often called ad hoc testing. The term ad hoc is often used interchangeably with random in software testing, but the two terms are not the same. Ad hoc testing may or may not be random, and it may or may not be systematic. Ad hoc means for a specific case only. An ad hoc test is a one-time-only test. The maze-traversing efforts of the Egyptian and Theseus were ad hoc, because neither one of them ever returned to do it again. In testing practice, the one-time-only criteria is too often used to justify not keeping any records and possibly not using any algorithms. After all, why invest in records or methods when the test will never be repeated? Because of this rationale, most ad hoc testing that is done is not reproducible.

The one-hand-on-the-wall method is systematic and reproducible. If the maze has not changed, the one-hand-on-the-wall method will always follow the same path. The tester can always turn around, put the other hand on the wall, and retrace steps to the entrance. This method is only ad hoc if the sacrificial person never has to go back into the maze again once he has found a way out. Unlike the Egyptian, software testers are dropped back into the maze regularly-every time there is new code.

Thus, the one-hand-on-the-wall method is not random; it is systematic, because each branch taken is based on static criteria-that is, always branch right or always branch left. Random simply means without specific order. Random tests can be reproducible. Tests that are generated at random can be documented or mapped and later reproduced. This brings us to the maze-traversing method used by Theseus, the Greek who slew the Minotaur.

Theseus was determined to stop the sacrifices to the Minotaur, and for that reason, he volunteered to enter the maze. Minos' daughter Ariadne had fallen in love with Theseus. She gave him a ball of thread, which he tied to the entrance of the maze and unwound as he wandered through the maze. Theseus found and killed the Minotaur, rounded up the sacrificial men and women, and followed the thread back to the entrance, where Ariadne lowered a rope for Theseus and the sacrifices to climb to freedom.

The technique that Theseus used to find the Minotaur was random, because he did not use a systematic method, such as putting one hand on the wall to determine his course. He simply followed his instincts till he found the Minotaur. Theseus' technique was ad hoc, because Theseus traced the path to the Minotaur only one time. The technique used by Theseus will work for any path in any maze with virtually any structure. If the string is not disturbed, the path can also be retraced at a later time, making it a reproducible random path.

Theseus succeeded and escaped the Minotaur's maze because he used the thread as a documentation tool that automatically kept track of the turns he made, allowing him to retrace his path back to the entrance. Clever testers typically use a key trap tool as their "ball of string." Testers may hope that they will never have to replay the test captured as they went; but if something breaks, they can at least try to reproduce the test.

An undocumented ad hoc test may be adequate if the test never needs to be repeated, but it falls short when the test finds a bug (which is, according to many experts, the whole reason for testing). To diagnose the bug, someone will have to reproduce it. If there is no repeatable method or string trail, then reproducing the problem can be virtually impossible. Even when such bugs do get fixed by development, when the fixes are delivered to test, the testers are not in a position to verify them because there is no way to retrace the path.

This is the core of what is wrong with ad hoc test efforts. The sacrificial testers are trying to get through the maze by running through it as fast as they can go-random and ad hoc-rather than using a systematic approach and marking their trail. If a tester is lucky enough to find the exit and if the director asks, "What did you test?" the answer is just about guaranteed to be, "I tested it."

By contrast, in the testing conducted in the prop-up-the-product-with-support scenario, discussed in Chapter 3, the support person gets to play the part of the hero Theseus and rescue the poor sacrificial customers from the monster bug in the maze. The support person's mission is clear: a bug exists and must be removed. Support does not need to know anything else about the maze. The most important distinctions between test and support personnel are that:

• The folks in the test group must go looking for bugs, while the users bring bugs to the folks in support.

• The folks in support are often empowered to fix the bugs they find, while the folks in the test group are not.

Note 

In software testing, we need to be able to identify and count the paths through the maze.

We use algorithms to identify and map paths, but we also need to be able to calculate the number of paths that exist in a given maze based on the properties of the maze. As the maze grows larger and the number of branching corridors increases, the potential for multiple paths to the exit also grows. If the maze does not conform to some rules, like the ones necessary for the Egyptian's method, then the number of paths through a maze can be virtually infinite, impossible to trace or map algorithmically and impossible to determine by calculation.

Webster's New World Dictionary defines a system as a set or arrangement of things related or connected so as to form a unity or organic whole. A structured system is a system or subsystem that has only one entry point and one exit point. The concept of structured programming was introduced many years ago to help limit the number of paths through a system and thereby control the complexity of the system. Essentially, structured programming gives the sacrificial testers a sporting chance, by guaranteeing that there will be only one way in and one way out of the maze, and no trapdoors or pits.

The fundamental path question for software testers is this: "How many paths are there through this system?" This number is, effectively, one of the two primary measures of "How big it is." If we can't establish this parameter, we have no benchmark to measure against. We have no way to quantify how big the project is, and we cannot measure what portion of the total we have accomplished. We will not be able to give a better answer than "I tested it."

The one-hand-on-the-wall approach alone does not answer the question, "How many paths are there?" The selection criteria are limited to all branches in a single direction. Random testing does not answer this question either. When paths are selected at random, there is no guarantee that all possible paths will be selected. Some paths will probably be selected more than once, while others won't be selected at all. To map all the paths through a system, the tester will need to follow a systematic set of algorithms.

Determining the number of paths through a maze empirically, by trial and error, can be very unreliable. Algorithms can be combined in order to trace all paths, one at a time, but this is time-consuming and virtually impossible to carry out in a large real-time system. In complex systems, a tester using these methods may never be able to prove that all possible combinations of paths have been traced. For the purpose of identifying paths, we introduce the concept of linear independence.

Linear Independence

Consider a line that is independent of other lines. For paths, this means only one trace or traversal for each path is counted. In a structured system with one entrance and one exit, where the object is to proceed from the entrance to the exit, this is the same as saying the following:

For any structured system, draw each path from the entrance of the system to the exit. Only count the path the first time you walk on it. In the process of traversing all the paths from the entrance to the exit, it may be necessary to retrace some path segments in order to reach a path segment that has never been traversed before, or to reach the exit. But a path through the system is linearly independent from other paths only if it includes some path segment that has not been covered before.

When a person becomes lost in the maze, he or she can potentially wander through the maze retracing steps until he or she dies. The paths followed by the wanderer are not linearly independent. A programming example of paths that are not linearly independent is a program that loops back to retrace the same path through the system, repeatedly. In that example, the total number of possible paths is potentially infinite. The program can get stuck in a loop until someone kills it. Another example is a logon screen with no functional cancel button, meaning the user cannot leave the logon screen until a correct and valid password and user ID have been entered. This will cause an infinite loop for any user who does not have a valid password and ID.

The path traces caused by looping, feedback, and recursion are only counted once as linearly independent paths, even though they may be retraced over and over again as different paths are traced through the system. In a program, how many times a loop is traced, along with how many times a recursive call is made, is controlled by data. When we build our test cases, we will add data sets to our linearly independent paths in order to exercise the data boundary conditions and the logic paths accessed by them. Some paths will be traversed many times because of the data that will be tested. The purpose of this exercise is to calculate the number of paths necessary to cover the entire system.

Let's take a look at two structures that are common in programming and some methods for counting the paths through them: the case statement and a series of required decisions.

The Case Statement

The case statement is particularly important for software application testers because it is the structure used in menus. Figure 11.3 shows a typical case statement structure. The maze analogy is a single room with several doorways in which every doorway leads eventually to the exit. The user has as many choices as there are doors. Where the program goes next is determined by the user's selection. The user makes one choice at a time and can always come back to the menu and make a different choice.

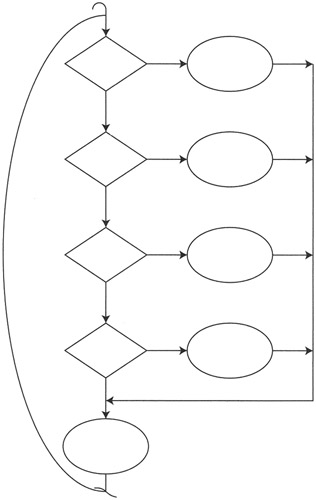
Figure 11.3: Case statement structure.

Linear Independence

As shown in Figure 11.4, there are five linearly independent paths through this example. We can identify them by inspection, tracing them visually one at a time. The first two paths, Paths 1 and 2, could be found using the left- and right-hand-on-the-wall method. Paths 3, 4, and 5 are the other linearly independent paths through this maze. Note: Traditionally, the exit arrow pointing down is the true condition.

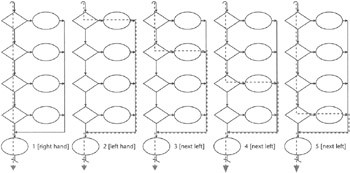
Figure 11.4: Five linearly independent paths.

We can also find the five paths by using the following algorithms.

ALGORITHM 1, PATH 1

1. Enter the system.

2. At every branch, select the true condition for each decision (right-hand) path until the exit is encountered.

ALGORITHM 2, PATHS 2, 3, 4, 5, AND 1

1. Enter the system.

2. Select the true (right-hand) path until the first branch where the false (left-hand) path has not yet been selected.

3. Take the false (left-hand) branch.

4. Thereafter, always select the true (right-hand) path until the exit is encountered.

Anyone who has studied data structures will recognize this method of traversing a tree structure. It is systematic and reproducible. Using this algorithm, the tester can reliably identify every path through this system. Other algorithms can be used to solve this problem. By using the systematic approach, we are sure of what we have done when we finish, and we can count the number of paths that go end-to-end through the system.

Algorithm 2 will find all five paths. Path 1, the all true (all right-hand) path will be found last, after all the false (left-hand) branches have been exercised. The reason it is presented with the shortest path as the first path identified is because this shortest path should be the most important path in this system from a tester's perspective. It is the quickest way out of the maze. If, for example, this same logic flow was behind the logon component of a vast and wonderful network, the most important path to both user and tester is the correct logon scenario. If this simplest and most direct true path does not work, what good is any other path?

In software, other criteria are used to define paths besides linear independence. Statement coverage and branch coverage are two examples and are described in the following paragraphs.

Statement Coverage

Statement coverage is a method of path counting that counts the minimum number of paths required to walk through each statement, or node, in the system. This number may or may not be the same as the linearly independent paths. In this example, the case statement, only paths 2, 3, 4, and 5 are required to satisfy 100 percent statement coverage. Note that a tester who only uses statement coverage as a basis has no requirement to exercise path 1, which is possibly the most important path.

Branch Coverage

Branch coverage is a method of counting paths that counts the minimum number of paths required to exercise both branches of each decision node in a system. In the case statement example, all five linearly independent paths are required to satisfy 100 percent branch coverage.

The case statement is a straightforward example. Now we will look at an example that is more complex.

In the case statement, the number of paths required for 100 percent coverage:

• Statement coverage = 4

• Branch coverage = 5

• Linearly independent path coverage = 5

• Total paths = 5

A Series of Required Decisions

This construct is important because it is common and it serves to illustrate how quickly the number of paths can become uncertain and confused. Figure 11.5 is a visual representation of such a construct. In this type of maze, each branching path leads back to the main path. There is only one branch that leads to the exit. The number of possible combinations of path segments that one could combine before reaching the exit becomes large very quickly. This is the type of processing that goes on behind some data entry screens. For example:

Are the contents of the first field valid? If they are, check the second field. If not, branch to the exception and then check the second field. Are the contents of the second field valid? If they are, check the third field. If not, branch to the second field's exception and then check the third field, and so on.

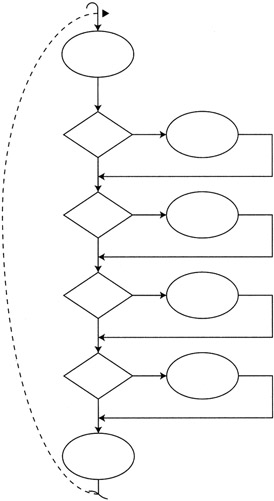
Figure 11.5: A series of required decisions.

When we use the left-hand method in Figure 11.6, we discover that we have already walked through each statement or node of the system in only one path traversal. Thus, 100 percent statement coverage can be accomplished in a single path. Branch coverage can be accomplished in two paths by exercising Path 1, the right- hand or all-true path, and Path 2, the left-hand or all-false path.

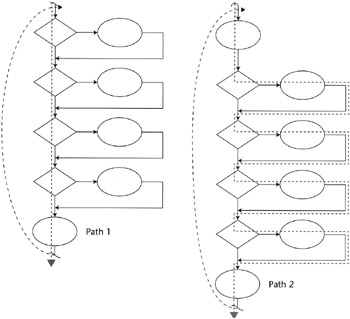
Figure 11.6: Paths 1 and 2.

This means that the tester who performs only 100 percent statement test coverage is missing 50 percent of the branch conditions. The tester performing only 100 percent branch test coverage is missing all the paths where true and false data conditions are mixed. Example: We have already discussed two paths through this maze; how many paths are there in total?

If-then-else-structure paths for 100 percent coverage:

• Statement coverage =1

• Branch coverage = 2

• Linearly independent path coverage = 5

• Total path coverage = 16

If we select only one branch at a time, we will find four linearly independent paths. Notice that Paths 1, 3, 4, 5, and 6 all traverse some path segments that have been traversed by the others, but each includes some path segment that is unique to that particular path. All of the right-hand or true paths are exercised across these four paths. Each left-hand or false path segment is covered one time. Paths 1, 3, 4, 5, and 6 are linearly independent from each other. Each contains path segments that are not covered by any of the others. Path 2 is not linearly independent from Paths 3, 4, 5, and 6 (see Figure 11.7).

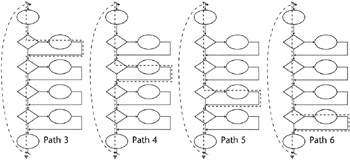
Figure 11.7: Paths 3 through 6.

If we select two branches at a time, we will find six more paths (see Figure 11.8).

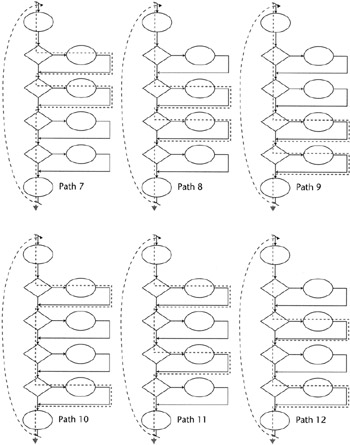
Figure 11.8: Paths 7 through 12.

If we select three left branches at a time, we will find the last four paths (see Figure 11.9).

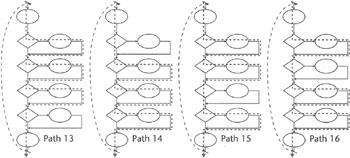
Figure 11.9: Paths 13 through 16.

This series of decisions, with four decision or branching nodes, has 16 paths through it. These paths represent all the combinations of branches that could be taken through this maze. If all of these 16 paths are exercised, several of the path segments will be retraced many times. A typical program contains hundreds of branching nodes.

We have been discussing program logic at the code level. We could just as easily be discussing the logical interaction between many programs in a software system. Both of the preceding examples were structured systems.

Note 

100 percent path coverage is beyond the resources of ordinary test efforts for all but the smallest software systems.

Given that a software system contains hundreds of logic branches, the number of paths in even a small software system is huge. Two things should be clear from this example. First, when we map every possible path, it becomes clear that while many paths segments are covered repeatedly, others may only be touched once. We won't have time to test them all. Second, even if we have time to test them all once, we won't have time to retest them all every time new code is turned over. We need to use rational criteria in order to pick our test sets.

Note 

It is not feasible to count the paths through such a system empirically or by inspection. What is really needed is a way to calculate the number of paths that exist in the system.