Trigonometry Functions

I l @ ve RuBoard

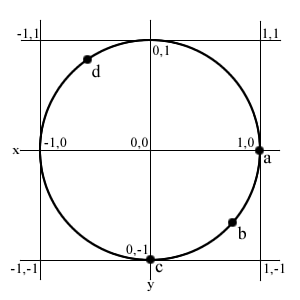
Most of the previous Math functions are easy to understand and use. However, you may not remember how to use the trigonometry functions such as sine and cosine.

Although it would be easy to just skip these functions, they are incredibly useful for creating animated effects. So I'll try to explain how they work.

The sine and cosine functions, referred to in ActionScript as Math.sin and Math.cos , represent the relationship between a straight line and the curve of a circle's circumference.

Figure 11.1 shows a circle with several points marked with letters . Imagine the center of the circle is at point 0,0. The radius of the circle is 1, so the top point is 0,1, and the rightmost point is 0,1.

Figure 11.1. This diagram shows a circle of radius 1 and several reference points on its circumference.

Imagine the circle as a line. It starts at point 1,0, labeled with an "a" in Figure 11.1. The line curves along to 0,-1, then to -1,0, then to 0,1, and finally back to 1,0. It is a long curved line.

In Flash, and just about any other computer program, we position things according to x and y coordinates. So being able to convert a point on the line of a circle into x and y coordinates can be useful.

This is what sine and cosine do. For instance, if you consider point "a" to be the beginning of the circle's line, you can plug 0 into cosine and sine functions to get the x and y coordinates of point "a." Sure enough, Math.cos(0) returns 1, and Math.sin(0) returns 0. That corresponds to the 1,0 location of point "a."

So where along the circumference of a circle is point "c"? Well, the line around a circle turns out to be 6.28 times its radius. So because its radius is 1, the line should be 6.28. This is where the magic number pi comes from. Pi is 3.14, which is half the distance around a circle.

So if 6.28 is the total distance around the circle, 1.57 should be a quarter of the total distance. That should correspond to point "c," which is a quarter of the way around the circle. Math.cos(1.57) is a very small number, pretty close to 0. Math.sin(1.57) is a number very close to -1. The reason they are very close, but not right on, is because pi is not exactly 3.14 ”it is just a close approximation .

So if point "a" is point 0 along the circle, and point "c" is 1.57 along the circle, then point "b" looks like it is about .785 along the circle, or halfway between points "a" and "c." So where is this in terms of x and y screen coordinates? Just plug.785 into Math.cos and Math.sin to get the answer. The result is .71,-.71, so it is .71 over to the right of center, and .71 down from center.

You can translate any point along the circle into x and y coordinates with this. Point "d" in Figure 11.1 is about 4.2 along the circle. This puts it at -.49 x and -.87 y, which looks about right according to Figure 11.1.

So how is this useful? Well, suppose that you want to make a movie clip fly around the screen in a circle. How would you do that? You could make dozens or hundreds of frames of animation. Or you could use Math.cos and Math.sin functions to calculate the x and y coordinates as the object moves around the circumference of the circle.

In the following script from example movie 11circle.fla, the movie clip moves along a circle of radius 100. The center of the circle is at 150,150.

As "n" increases , the movie clip moves along the circumference of the circle. Math.cos calculates the corresponding x coordinate, and Math.sin calculates the y coordinate. They are each multiplied by radius to make a bigger circle. The variables centerX and centerY are added to the coordinates so that the center of the circle is at 150,50 rather than 0,0.

 onClipEvent(load) {     n = 0;     radius = 100;     centerX = 150;     centerY = 150; } onClipEvent(enterFrame) {     n += .1;     this._x = Math.cos(n) * radius + centerX;     this._y = Math.sin(n) * radius + centerY; } 

Notice that as "n" gets bigger, it passes 6.28, the total length of the line around the circle. This is okay because the Math.cos and Math.sin functions will handle the larger numbers . So 7.28, which is about 1 past the total circumference, will give the same results as 1.

I l @ ve RuBoard