FINDING THE OPTIMAL SET OF MATERIALIZATIONS
|
|
When using materialized views in a MDDB, the most important problem to solve is to find the set of materializations that maximizes the performances of the MDDB in answering a given set of representative queries. The trade-off consists of choosing a set of materializations able to speed up query response time without requiring too much work to keep the materializations current with respect to the modifications on the tables of the MDDB.
Definition 13: Given an MDDB DB, a set of queries Q, and a set of frequency values F of queries in Q and updates on the tables of DB, the MDmat-problem (multidimensional database materialization problem) is represented by Θ(DB, Q, F). A solution to the problem Θ(DB, Q, F) is a set of views of the MD-lattice M (which can contain views that are not associated with queries in Q). A trivial solution, M = Ø, is always possible, which represents the situation where no additional materialization is available and all the queries must be answered directly by the fact table (the root of the hierarchy).
To identify the optimal M, we must define a cost function. The optimal solution is the one characterized by the minimum cost. The cost function is composed of two parts: the query cost and the update cost.
Definition 14: Consider a set of queries Q specified by the user. Let F be a set of frequencies f q i , each associated with a query qi ∊ Q, representing the frequency with which query qi is asked. Let cqi (M) be the cost to compute qi from the set of materializations M (discussed in the second section).
Then, the total query cost CQ(Q, M, F) is given by:
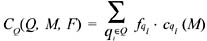
Definition 15: Consider the same set of materialized views M. Let f m i be the frequency with which the materialized view mi ∊ M is modified and cu (mi ) its update cost. Then, the total update cost CM(M, F) is given by:
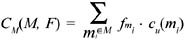
Definition 16: Given an MDmat-problem described by Θ(DB, Q, F), the cost of a solution M is the sum of query and update costs:
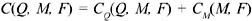
Query Cost
We do not present here a complete cost model. The techniques we describe are applicable to a wide choice of cost models, from simple to complex ones. Very few restrictions have to be imposed on the cost formulas to permit the adoption of our results.
The function c q i(M) returns the cost of computing query qi given a set of materializations M. We make two hypothesis about the query cost function: that each query cost depends on a unique element in M, and that the cost is monotonic with the size of the materialization on which the query depends.
Definition 17: A query cost function cqi (M) is restrictible if it is always equal to the least among the values obtained by considering c q i (mj ), for all the mj ∊ M on which query qi depends.
Every query of the type introduced in the fourth section of this chapter is restrictible (since the fact table is always present in the set of materializations).
Definition 18: Given a query qi , a restrictible query cost function cqi , and a set of materializations M, the materialization mj such that cqi(M)= cqi(mj) is the least expensive materialization (for query qi among the elements of M).
Definition 19: A query cost function cqi (MD-lattice) is monotonic if for all vj , vk ∊ MD-lattice on which qi depends, |vj| < |vk| → cqi(vj) ≦ cqi(vk), where |v| represents the cardinality of v and the arrow denotes logical implication. From the observation on the cardinalities of the views in the lattice, a monotonic function also guarantees that vj≼vk → cqi(vj) ≦ cqi(vk).
The simple cost model introduced in Harinarayan, Rajaraman, & Ullman (1996) is, for example, both restrictible and monotonic: the cost of answering a query q is set equal to the number of tuples read to return the answer. This cost model, although very simple, well characterizes the problem. An extension of this model permits consideration of the availability of indexes to accelerate the execution of queries, as described in Gupta et al. (1997). We do not treat indexes here, but a technique similar to Gupta et al.'s (1997) can be applied in this context as well, as it is also demonstrated in Agrawal, Chaudhuri, & Narasayya (2000).
The extension to an MDDB and join operations may require modification of this simple metric, which is still adequate when it is possible to keep in memory all the dimensions involved in the join. In fact, in this case the join requires reading only once all the tuples, and since the cardinality of the fact table is greater than that of any dimension, often by several orders of magnitude (Kimball, 1996), the cost of performing a join operation between any dimension and the fact table F can be modeled as the cost of reading F. When the join is more complex, a different cost function may be required. Sophisticated cost functions can be designed which adequately model this aspect of the system and still respect the requisites of restrictibility and monotonicity.
The cost of performing a group-by operation can be modeled as the cost of reading the table or materialized view on which the grouping is computed. This hypothesis does not consider the sort order which is used to store each materialization (see Agarwal et al., 1996), which has a relevant impact on the complexity of computing the aggregations; this aspect can also be modeled by a restrictible and monotonic cost function.
Identification of Candidate Views
Compared to the number of nodes that form the MD-lattice, the number of representative queries is extremely small. This considerable sparsity of queries among the views of an MD-lattice suggests that only some of these views are relevant when deciding which views to materialize in order to minimize the total cost. The idea of our reduction technique is to consider only those views of an MD-lattice that, when materialized, can provide some contribution to reduce the total cost. We call them candidate views, and define them as follows.
Definition 20: A view vi belonging to an MD-lattice is a candidate view if one of the following two conditions holds:
View vi is associated with some query qi.
There exist two candidate views vj and vk, such that vi is the least upper bound (l.u.b.) of vj and vk.
Note that, from the previous definition, it follows that non-candidate views do not have an associated query.
Definition 21: Given a non-candidate view vi with at least one candidate view depending on it, we call most directly dependent candidate view the unique candidate view vj such that all the remaining candidate views that depend on vi also depend on vj.
We can determine the most directly dependent candidate view of vj by taking the set V′ of all the candidate views that depend on vj and computing the l.u.b. of all the views in V′. This view is unique (because an l.u.b. is always determined), is a candidate view (because it is an l.u.b. of candidate views), and belongs to V′ (because va ≼ vi ∧ vb ≼ vi → (va ⊕ vb) ≼ vi).
Intuitively, it is not difficult to see that candidate views may provide some benefit if they are chosen to be materialized. If the view is associated with a query, materializing it will decrease the total cost if the increment of the update cost is compensated by the reduction on the query cost. When the view is the l.u.b. of other candidate views vj and vk, which may be associated with queries qj and qk, the total cost will be minor if the cost needed to answer qj and qk using a materialization of vi is compensated by the reduction on the update cost of the materializations of vi and vj. We can analyze more formally these properties.
Let vi be a candidate view of an MD-lattice. Then, choosing vi for materialization may provide some benefit when looking for the solution that reduces the total cost. There are in fact two cases:
-
vi has an associated query qi.
It is trivial to show that the materialization of a view associated with a query can help the computation of the query. Starting from the definition of the cost of a solution, we obtain the following formula, which identifies the query frequency value f q i that makes convenient the materialization of view vi when a set of views M is already materialized:
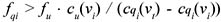
vt ∊ M represents the least expensive materialization that can be used to answer qi.
-
There exist at least two candidate views, vj and vk, such that vi is the l.u.b. of vj and vk.
It is enough to show that there exists at least one case in which materializing vi provides some benefit. Assume that there exist two queries qj and qk associated with views vj and vk, respectively. The contribution of queries qj and qk and views vj and vk to the cost C(Q, M, F), when vj and vk are materialized and vi is not, is:
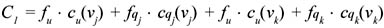
The contribution to the cost C(Q, M, F) if vi is materialized and vj and vk are not, with vi being the least expensive materialization for both qj and qk, is:
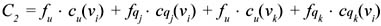
Choosing vi for materialization will decrease the total cost if C1 > C2, i.e., when:
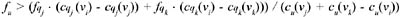
with the hypothesis that cu(vj)+ cu(vk)− cu(vi) > 0. The intuition is that if the cost of updating views vj and vk is greater than the cost of updating vi, for a high enough update frequency fu,, it may be convenient to materialize view vi instead of vj and vk.
Moreover, if we want to ensure that candidate views are the only relevant views for the process of deciding which views to materialize, we must prove also that materializing a non-candidate view may never decrease the total cost. This is done in Theorem 1.
Theorem 1: Let vi be a non-candidate view of an MD-lattice. Then, the choice of vi for materialization is always dominated by the choice of a candidate view.
Proof: We will assume that there exists a non-candidate view vi that belongs to the set of materializations M of the optimal solution, and we will get a contradiction. We distinguish two cases.
-
There is no candidate view depending on vi.
The contribution of view vi to the cost C1 = C(Q, M, F) of the solution M for Θ(DB, Q, F) (vi ∊ M) is represented only by the contribution to the update cost fu · cu(vi), since no query can use vi (otherwise there would be candidate views depending on vi). The cost of the solution M−vi is equal to C2 = C(Q, M−vi , F), where C1 = C2+fu · cu(vi). Since materializing vi must provide some benefit, it must happen that C1 < C2, i.e., fu · cu(vi)< 0. Then, we get a contradiction because both fu and cu(vi) must be positive.
-
There exists at least one candidate view depending on vi.
We first identify view vj, the most directly dependent candidate view of vi. We then consider separately two sub-cases, represented in Figures 4 and 5.
Figure 4: A Configuration of Materializations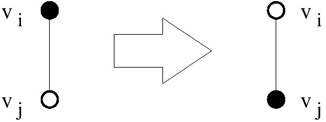
Figure 5: A Configuration of Materializations
Case 1: Both vj and vi are materialized (represented in Figure 4). Let M′ = M −vi −vj. The cost of this solution is:

We observe that view vi is not used by any query qi ∊ Q, because all the queries that depend on vi also depend on vj, and since vi≼ vj, it follows that cqi(vi)> cqi(vj). We can then remove it from the first term of the formula for C3 obtaining:
![]()
The cost of the solution with materialization M′ ∪ vj is:
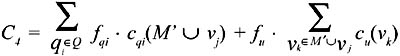
The difference between C3 and C4 is represented by the single term fu · cu(vi). In order for C3 to be the optimum (i.e., C3 < C4), it must happen that fu · cu(vi)< 0. We get a contradiction since both fu and cu(vi) must be positive.
Case 2: vi is materialized and vj is not (represented in Figure 5). Let M′ = M − vi. The cost of this solution is:
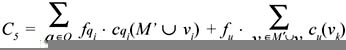
In particular, this solution must be better than the solution where vj is materialized but vi is not, which has the cost C4 defined in the above formula. But each term c q i (M′ ∪ vj ) in C4 must be less than cqi (M′ ∪ vi ) in C5 , because all the queries that depend on vi must also depend on vj ; vj is smaller than vi and the query cost function is monotonic. Term cu (vj ) must also be smaller than cu (vi ), for the monotonicity of update cost with view size. It is then impossible for C5 to be smaller than C4.
Once we have proven that candidate views are the only views that are relevant to the process of deciding which materializations minimize the total cost, we can define the sub-lattice obtained by considering only candidate views.
Definition 22: Given an MD-lattice and a set of queries Q, the set of its candidate views identifies also a lattice where the join and meet operations are identical to the ones defined for the MD-lattice. We call this sub-lattice the MDred-lattice.
Given a set Q of queries and the MDDB attribute hierarchy, we can identify all the elements of the MDred-lattice. This is performed by means of the following algorithm.
Algorithm 3: The MDred-Lattice Construction Algorithm

Algorithm 3 iteratively extends the set L. L is initially equal to the set of views in Q. The l.u.b. of all the pairs of elements in L are added to L, and the process iterates by considering the l.u.b. of all the pairs of views obtained by combining the new elements of L with all the elements of L, until a fixpoint is reached where no new l.u.b. can be added to L.
It is now convenient to describe another technique based on statistical estimates of the size of the materializations. Given its statistical foundation, the next technique is not as exact as the one just presented.
A Heuristic Reduction
When building the MDred-lattice, a simple heuristic technique can be used to further reduce the size of the lattice, removing views which are not expected to contribute to the optimal solution. This heuristics is based on the estimate of the size of the materialization. These estimates can be done following traditional query estimation techniques for aggregates. If the skewness of data is of concern, it is also possible to use the technique, described in Shukla et al. (1996), which obtains an estimate of the number of tuples that is quite precise for a wide range of skewness in the distribution.
According to the estimates on the size of views, it is possible to determine when the level of aggregation used is too detailed and the materialization offers very limited help in answering the query with respect to a materialization of a higher level view.
Example 6: Consider a dimension A with 1,000 tuples. Let a view contain an aggregation for the pair of attributes {A1 , A2}, where each attribute has 100 distinct values. There are 10,000 possible pairs of values of the attributes, but since there are only 1,000 tuples, at most 1,000 tuples can be present in the view. If the data is uniformly distributed, the estimate of the size of the view is quite close to 1,000. Instead of materializing this view, it could be convenient to use the view which has the key of dimension A as aggregating attribute. The great advantage is that it will be easier to reuse this view in the computation of other aggregates and the number of elements of the lattice will be, in general, reduced.
We can easily modify the MDred-lattice construction algorithm to estimate at each step the dimension of a view, and substituting to it a higher level view if the reduction criteria are not met. In the next section we illustrate a few experimental results. We now describe more formally this technique.
Definition 23: A size estimating function size(A)is a function that, applied to a set of attributes A of an MDDB, returns an estimate of the number of tuples of the result of an MDDB query q characterized by A (i.e., having A as grouping attributes).
Definition 24: A size estimating function is correct if for all the functional dependencies fdi ∊ FDDB, size(Ari) ≠ size(Ali).
Intuitively, since there exists a functional dependency Ali → Ari, for each combination of values of Ali, more than one combination of values for the attributes in Ari cannot exist. Thus, a query grouping on Ali cannot have more tuples than a query grouping on Ari.
Algorithm 4: Heuristic Reduction Algorithm

Algorithm 4 considers all the functional dependencies to identify when the attributes in A that appear on the right side (or a subset of them) of a functional dependency produce a size estimate which does not differ more than a ratio ρ from the estimate of the size of the attributes on the left side. When this happens, the attributes on the right side are replaced by the attributes on the left side, effectively moving from a view vi characterized by the set of attributes A to a view vj≼ vi.
The parameter ρ represents the threshold on the amount of reduction in size above which the left side of a dependency should be used in place of the right side. The user should determine this value, depending on a trade-off between accuracy of the solution and reduction in the size of the solution space. Even high levels (e.g., r = 0,95) can be quite effective in simplifying the solution space.
|
|
EAN: 2147483647
Pages: 150