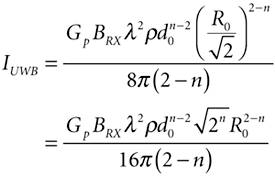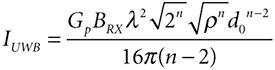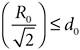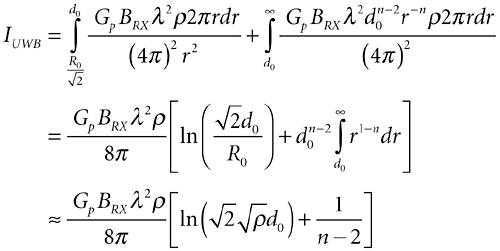Section A.2. GPS Receivers
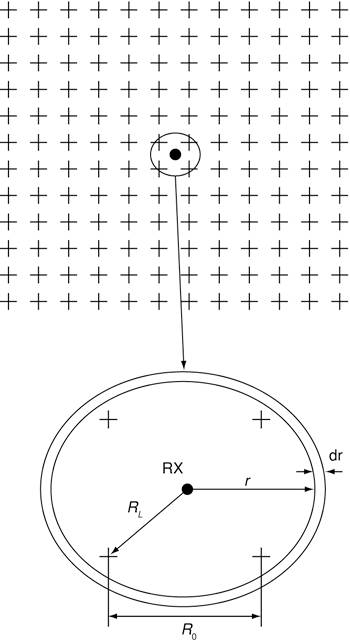
A.2. GPS ReceiversAs in the previous section, we revisit the interference scenario considered in Figure 4-23 (here reproduced as Figure A-2) to describe the parameters used to derive equations for theoretical interference analysis of UWB systems on GPS receivers. Figure A-2. Interference scenario of multiple UWB sources on a GPS receiver
The top half of the diagram in Figure A-2 shows multiple UWB transmitters, denoted by crosses, distributed about a 2D plane, and a cellular receiver at the position marked by a black dot. The bottom diagram is an enlarged version of the center of the top diagram, and it shows some of the dimensions required for the derivation of the interference power from the UWB transmitters to the receiver. The total interference power at the receiver from the UWB transmitters, IUWB, can be calculated by evaluating the following integral: Equation A-9
where Pr is the received power from a UWB transmitter located at a distance r from the receiver. The distance from the receiver to the nearest UWB transmitters is RL, which can be expressed in terms of the average distance between UWB transmitters, R0, by Equation A-10
The received power can be approximated by Equation A-11
where P0 is the power received at a free space reference distance d0 in the far-field region of a UWB transmitting antenna, and n is the path loss coefficient. It is appropriate to assume a d0 of 100 meters for urban macrocells. P0 can be expressed as Equation A-12
Therefore, the total interference power at the receiver can be expressed as Equation A-13
Now provided 2 > n, the interference power is Equation A-14
Given that for 2 > n,
as r Equation A-15
The average distance between UWB transmitters is related to the density of UWB transmitters by Equation A-16
Hence, the interference power, IUWB, can be expressed as a function of the density of UWB transmitters: Equation A-17
For UWB transmitters distributed with density r such that
is less than or equal to d0, then free-space propagation can be assumed from UWB transmitters within a distance of d0 from the cellular receiver. The preceding condition,
can be rewritten as
When this condition is true, Equation A-9 becomes Equation A-18
A general expression for the UWB interference can be formulated by combining Equations A-17 and A-18: Equation A-19
where Gp denotes the ultra-wideband power spectral density, BRX represents the victim receiver's bandwidth, and F(l, r, d0, n)is described by Equation A-20
|
EAN: 2147483647
Pages: 93
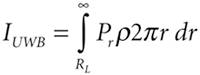
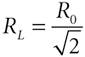
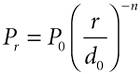
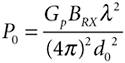
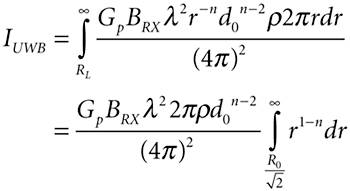

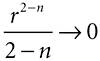

 , then the interference power at the receiver is
, then the interference power at the receiver is