Section 10. Control Charts

10. Control Charts

Overview

Most novice Belts confuse Statistical Process Control (SPC) with Control Charts and vice versa.^[15] SPC is the use of Control Charts to help control a process. Control Charts are used in a number of places in the Lean Sigma roadmap to test whether a process is stable and in control, that is having

^[15] Use of Control Charts for Process Control dates back to the 1920s and Dr. Walter Shewhart of Western Electric.

• Consistent centering (typically the mean)

• Predictable variation

For example, the tool is used

• To test for stability before performing a Capability Study in the Measure Phase

• To test stability before performing a test of means in the Analyze Phase

• In Statistical Process Control in the Control Phase

• To validate stability after project completion

SPC, on the other hand, is solely a Control tool and appears only in the Measure Phase (to check what is currently being controlled) and the Control Phase (to control what should be controlled going forward).

Control Charts^[16] typically take the form shown in Figure 7.10.1. Data is plotted over time across the x-axis, with the height on the y-axis representing the level of the characteristic in question. For example, if the Control Chart were placed on the purity of end product, then the y-axis would be Purity.

^[16] For extensive detail on the structure and theory of Control Charts see Statistics for Management and Economics by Keller and Warrack.

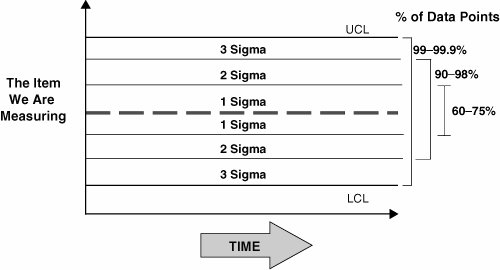
Figure 7.10.1. Structure of a Control Chart.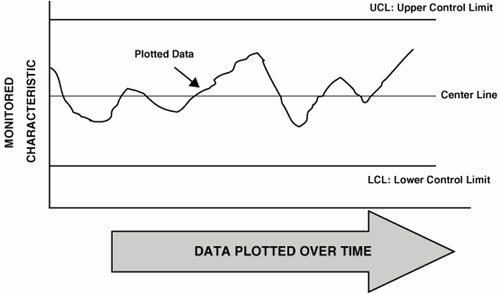

From the data in the chart, Control Limits are calculated and represent the boundaries of likely behavior within the process. A point landing outside of these boundaries is considered out of the ordinary. The Control Limits are calculated from the process data itself and depend on the data type.

For example, if the sample data from the process is Continuous and furthermore is normally distributed, then it is possible to predict where points should lie on the Control Chart applied to the sample as per Figure 7.10.2. The Control Chart used in this case is known as an Individuals Chart. The figure shows that by plotting the data there would be expected numbers of data points within certain bands given by the standard deviations from the center line (mean) as follows:

• From 1 to +1 standard deviations either side of the mean68% of data points (6075% in practice)

• From 2 to +2 standard deviations either side of the mean95% of data points (9098% in practice)

• From 3 to +3 standard deviations either side of the mean99.73% of data points (9999.9% in practice)

The lines at ±3 standard deviations are known as Control Limits, and an expected 99.73% of the process variation is expected to fall between these limits. In other words, the likelihood of seeing a point outside of these limits is 0.27% or about 370:1 against. This is considered an unusual event. Obviously in a process that generates hundreds or even thousands of entities, the occasional point falls outside the lines. Two in a row almost guarantees that something highly unusual has occurred or that the process has changed in some way (the foundation of SPC).

Figure 7.10.2. Distribution of data points with respect to standard deviations in a Normal Distribution.

There are other unusual occurrences that could be detected using the data distribution in Figure 7.10.2 with odds greater than 250:1 against

• Nine points in a row on the same side of the center line

• Six points in a row all increasing or decreasing

• Fourteen points in a row alternating up and down

• Two out of three points more than two standard deviations from the center line on the same side

• Four out of five points more than one standard deviation from the center line on the same side

• Fifteen points in a row within one standard deviation of the center line on either side

• Eight points in a row more than one standard deviation of the center line on either side

There are probably more that could be dreamt up, but these are the ones found in most statistical packages. Fortunately, none of these tests have to be run by hand; the statistical software package does this automatically and highlight any points that break the rules.

Stability is determined by having

• Consistent centering (typically the mean)

• Predictable variation

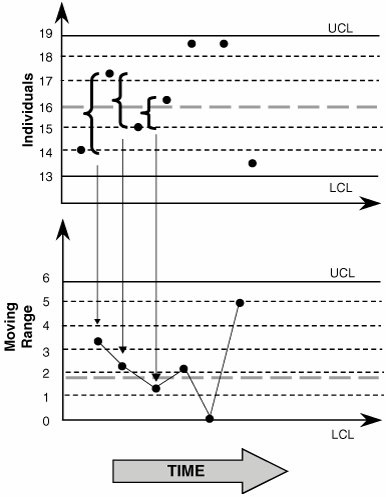
The Individuals Chart primarily tackles the former of these. To cater for the variation element, a Moving Range Chart usually accompanies the Individuals Chart. As shown in Figure 7.10.3, the Moving Range Chart shows the distance between adjacent points from the Individuals Chart. If there is a small change in the Individuals Chart, then the point on the Moving Range Chart is lower; if there is a large change, then the point is proportionately higher. If there is a very large change, then an unusual event has occurred and the point would register out of the Upper Control Limit (UCL). Similar to the list of unusual events for the Individuals Chart, the Moving Range Chart has its equivalent set.

Figure 7.10.3. Relationship between the Individuals Chart and the Moving Range Chart.

Together the Individuals Charts and Moving Range Charts express both characteristics of stability (centering and variation), so they are generally found together as a pairing known as Individuals and Moving Range or I-MR.

The Individuals Chart and Moving Range Chart are only two of many types of Control Charts. The Chart used for a particular application depends on the data type of the sample it represents.

Roadmap

The roadmap to select the appropriate Control Chart is shown in Figure 7.10.4 and is based on the data type of the sample concerned (for more information see "KPOVs and Data" in this chapter):

Figure 7.10.4. Control Chart selection roadmap.

• Continuous. The data is continuous (measured). Data of this type results from the actual measuring of a characteristic, such as diameter of a hose, electrical resistance, weight of a vehicle, and so on. Continuous data has two classifications of its own:

  • Individuals Data points are captured and recorded individually.

  • Groups Data points are captured in groups of, for example, five entities and recorded together. An explanation of why this is useful is given in "Other Options" in this section.

• Attribute. The data is discrete (counted). Data of this type results from using go/no-go gages, or from the inspection of visual defects, visual problems, missing parts, or from pass/fail or yes/no decisions. Attribute data has two classifications of its own:

  • Defect An individual error on an entity (scratch, blemish, a typographical error, and so on).

  • Defective The whole entity is not acceptable to the Customer. One defective entity might have multiple defects.

Interpreting the Output

As mentioned in "Overview" in this section, all Controls Charts take on the same form as shown in Figure 7.10.1. An example Control Chart for calls going to a call center is shown in Figure 7.10.5. The data type in this case is Attribute, defective items are being measured (the whole call), and there is a varying sample size (total number of calls in a period). So from the roadmap in Figure 7.10.4, the Control Chart used is a P-Chart.

Figure 7.10.5. P-Chart of callers needing assistance from a varying Total Number of Calls (output from Minitab v14).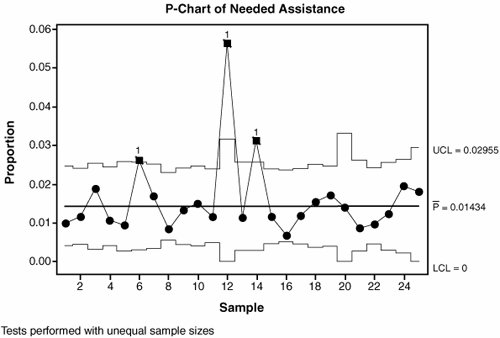

Although the Control Limits are not horizontal straight lines (due to the varying sample size), the way to read the chart is exactly the same as any other. If data points lie outside the Control Limits (points 12 and 14 for example), then something unusual occurred at that point in time (and similarly for any of the other "unusual" conditions listed in "Overview" in this section).

The key to understanding Control Charts is an appreciation of the different types of variation in a process,^[17] specifically:

^[17] A wonderful reference here, written in plain language rather than Statspeak, is Donald Wheeler's book Understanding VariationThe Key to Managing Chaos.

• Common Cause. The inherent variation present in every process, produced by the process itself. This is effectively the background noise in the process and is removed or lessened only by a fundamental change in the process, usually the process physics, chemistry, or technology. A process is Stable, Predictable, and In-Control when only Common Cause variation exists in the process.

• Special Cause. The unpredictable variation in a process caused by a unique disturbance or a series of them. Special Cause variation is typically large in comparison to Common Cause variation, but it is not part of the underlying physics of the process and can be removed or lessened by basic process control and monitoring. A process exhibiting Special Cause variation is said to be Out-of-Control and Unstable.

Thus, Control Charts are used to find the signals (special cause variation attributable to assignable causes) in amongst all of the background noise (common cause variation).

The biggest mistake Belts and Champions make is to confuse Control Limits with Specification Limits. Control Limits are calculated based on data from the process itself, they are not determined by anyone but the process itself. Product Specification Limits are not found on a Control Chart at all. Understanding how the process matches up against Customer requirements is important to know though and this is done with a separate tool called Process Capability.

Other Options

Control Charts are based on an understanding of where data points should lie and thus indicating if, for some reason, points seem to be out of place. This clearly relies on an ability to know where data points should lie. This is typically done from known distributions, such as the Normal Distribution for the Individuals Chart, or a Binomial or Poisson Distribution for Attribute type data. The difficulty arises when the distribution of the data doesn't fit a standard.

To counter this, there is a useful tool in statistics called the Central Limit Theorem,^[18] which relates to taking small groups of data points together rather than examining points individually. These small groups are known as subgroups. The useful property here, which stems from the Central Limit Theorem, is that even if the process itself is creating non-Normal data, the means of subgroups from the data is approximate normal data. This might be strange but it is true and extremely useful across many statistical tests.

^[18] For more information, see Statistics for Management and Economics by Keller and Warrack.

This is useful to the Control Chart because, rather than taking data and dealing with its strange distribution, perhaps having to transform it (to make it Normal) and then plotting a Control Chart from it, it is actually possible to take small subgroups of, for example, five data points and plot the means of the subgroups instead. The means tend to be more Normally distributed and the Control Chart is actually valid. This type of Control Chart is known as an X-bar Chart (the reason being that the symbol for the mean of a sample is an X with a bar over it). In fact another property of the Central Limit Theorem also takes effect here. The Control Limits (±3 standard deviations) are tighter on an X-bar Chart than would be expected for the raw individuals data,^[19] but don't worry about how the Control Limits are calculated, just use the Chart.

^[19] From the Central Limit Theorem, the variation in the means of subgroups is smaller by a factor of (where n is the subgroup size), so for a subgroup size of 5, the variability in the means is of the variability in the individual data points.

As mentioned previously, stability relies on two properties:

• Consistent centering (typically the mean)

• Predictable variation

The X-bar Chart takes care of the first of the two conditions; the second is usually done with a Range Chart. The Range Chart plots the actual range of the data in each subgroup (maximum minus minimum values) instead of a Moving Range as in the IM-R. The two graphs together become the Xbar-R Chart, see Figure 7.10.6.

Figure 7.10.6. An example of an Xbar-R Chart (output from Minitab v14).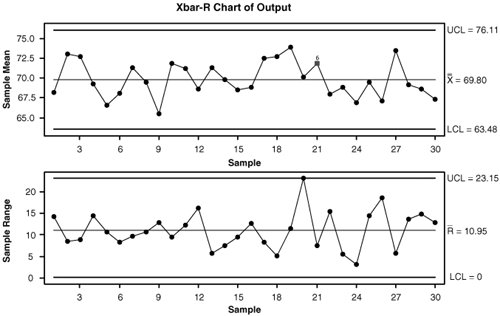

The first point in the top graph (X-bar Chart) is actually the mean of the points 1 to 5; the second point is the mean of the points 610, and so on. The first point in the bottom graph (Range Chart) is the range of the points 15; the second is the range of the point 610, and so on.

It might seem complicated at first, but it is easier to manage in practice for Statistical Process Control than a complex transformation. The Control Chart is interpreted just the same way as any other.