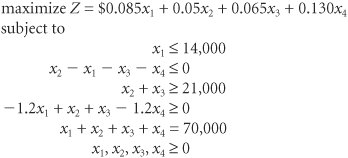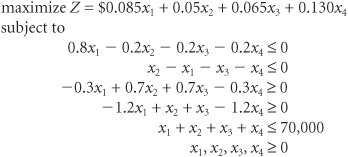An Investment Example | Introduction to Management Science (10th Edition)

[Page 119 ( continued )]

Kathleen Allen, an individual investor, has $70,000 to divide among several investments. The alternative investments are municipal bonds with an 8.5% annual return, certificates of deposit with a 5% return, treasury bills with a 6.5% return, and a growth stock fund with a 13% annual return. The investments are all evaluated after 1 year. However, each investment alternative has a different perceived risk to the investor; thus, it is advisable to diversify. Kathleen wants to know how much to invest in each alternative in order to maximize the return.

The following guidelines have been established for diversifying the investments and lessening the risk perceived by the investor:

No more than 20% of the total investment should be in municipal bonds.
The amount invested in certificates of deposit should not exceed the amount invested in the other three alternatives.
At least 30% of the investment should be in treasury bills and certificates of deposit.
To be safe, more should be invested in CDs and treasury bills than in municipal bonds and the growth stock fund, by a ratio of at least 1.2 to 1.

Kathleen wants to invest the entire $70,000.

Decision Variables

Four decision variables represent the monetary amount invested in each investment alternative:

x ₁ = amount ($) invested in municipal bonds

x ₂ = amount ($) invested in certificates of deposit

x ₃ = amount ($) invested in treasury bills

x ₄ = amount ($) invested in growth stock fund

The Objective Function

The objective of the investor is to maximize the total return from the investment in the four alternatives. The total return is the sum of the individual returns from each alternative. Thus, the objective function is expressed as

[Page 120]

maximize Z = $0.085 x ₁ + 0.05 x ₂ + 0.065 x ₃ + 0.130 x ₄

where

Z	=	total return from all investments
0.085 x ₁	=	return from the investment in municipal bonds
0.05 x ₂	=	return from the investment in certificates of deposit
0.065 x ₃	=	return from the investment in treasury bills
0.130 x ₄	=	return from the investment in growth stock fund

Management Science Application: The Evolution of the Diet Problem

When George Dantzig developed the simplex method for solving linear programming models, he illustrated the new technique by using the "diet problem" developed in 1945 by George Stigler. The problem was to determine a menu of foods that would satisfy nutritional requirements at a minimum cost. The diet problem has evolved over the years and continues to be a popular application of linear programming as institutional feeding programs at hospitals , military installations, nursing homes , schools , prisons, shelters, and restaurants have proliferated. Menu planning represents a formidable problem, with more than 30 nutritional constraints and thousands of variables, as well as consumer food preferences. Recommended daily allowances include minimum levels of 29 nutrients, while various health groups recommend maximum daily levels of fat, cholesterol, and sodium. Today, software packages are available for menu planning, including computer-assisted menu planning (CAMP), part of the IBM contributed programs library.

CAMP has had numerous reported applications around the world, including the development of a 90-day planned menu cycle at a state hospital and planned menus for schools that lower fat content while meeting nutritional requirements at a lower cost. In general, mathematical programmingbased meal planning models have been formed to reduce food costs by approximately 10% while meeting government-established nutritional standards. Other traditional menu planning methods have generally not achieved this level of success.

Source: L. M. Lancaster, "The Evolution of the Diet Model in Managing Food Systems," Interfaces 22, no. 5 (SeptemberOctober 1992): 5968.

Model Constraints

In this problem the constraints are the guidelines established for diversifying the total investment. Each guideline is transformed into a mathematical constraint separately.

The first guideline states that no more than 20% of the total investment should be in municipal bonds. The total investment is $70,000; 20% of $70,000 is $14,000. Thus, this constraint is

x ₁ $14,000

The second guideline indicates that the amount invested in certificates of deposit should not exceed the amount invested in the other three alternatives. Because the investment in certificates of deposit is x ₂ and the amount invested in the other alternatives is x ₁ + x ₃ + x ₄ , the constraint is

[Page 121]

x ₂ x ₁ + x ₃ + x ₄

This constraint is not in what we referred to in Chapter 3 as standard form for a computer solution. In standard form, all the variables would be on the left-hand side of the inequality ( ), and all the numeric values would be on the right side. This type of constraint can be used in Excel just as it is shown here; however, for solution with QM for Windows, all constraints must be in standard form. We will go ahead and convert this constraint and others in this model to standard form, but when we solve this model with Excel, we will explain how the model constraints could be used in their original (nonstandard) form. To convert this constraint to standard form, x ₁ + x ₃ + x ₄ must be subtracted from both sides of the sign to put this constraint in proper form:

x ₂ x ₁ x ₃ x ₄

Standard form requires all variables to be to the left of the inequality and numeric values to the right .

The third guideline specifies that at least 30% of the investment should be in treasury bills and certificates of deposit. Because 30% of $70,000 is $21,000 and the amount invested in certificates of deposit and treasury bills is represented by x ₂ + x ₃ , the constraint is

x ₂ + x ₃ $21,000

The fourth guideline states that the ratio of the amount invested in certificates of deposit and treasury bills to the amount invested in municipal bonds and the growth stock fund should be at least 1.2 to 1:

[( x ₂ + x ₃ )/( x ₁ + x ₄ )] 1.2

This constraint is not in standard linear programming form because of the fractional relationship of the decision variables, ( x ₂ + x ₃ )/( x ₁ + x ₄ ). It is converted as follows :

Standard form requires that fractional relationships between variables be eliminated .

Finally, the investor wants to invest the entire $70,000 in the four alternatives. Thus, the sum of all the investments in the four alternatives must equal $70,000:

x ₁ + x ₂ + x ₃ + x ₄ = $70,000

Model Summary

The complete linear programming model for this problem can be summarized as

Computer Solution with Excel

The Excel spreadsheet solution for the investment example is shown in Exhibit 4.7, and its Solver window is shown in Exhibit 4.8. The spreadsheet is set up very similarly to the spreadsheet for our product mix example in Exhibit 4.1. The decision variables are located in cells B13:B16 . The total return ( Z ) is computed in cell B17, and the formula for Z is shown on the formula bar at the top of the spreadsheet. The constraint formulas for the investment guidelines are embedded in cells H6 through H10. For example, the first guideline formula, in cell H6, is = D6*B13 , and the second guideline formula, in cell H7, is = D7*B13+E7*B14+F7*B15+G7*B16 . (Note that it would probably have been easier just to type the guideline formulas directly into cells H6 through H10 rather than create the array of constraint coefficients in D6:G10 ; however, for demonstration purposes, we wanted to show all the parameter values.)

[Page 122]

Exhibit 4.7.

Exhibit 4.8.

As mentioned earlier, it is not necessary to convert the original model constraints into standard form to solve this model using Excel. For example, the constraint for certificates of deposit, x ₂ x ₁ + x ₃ + x ₄ , could be entered in the spreadsheet in row 7 in Exhibit 4.7 as follows. The value, 1, the coefficient for x ₂ , could be entered in cell E7, = E7*B14 could be entered in cell J7, and the remainder of the constraint to the right side of the inequality could be entered as = B13+B15+B16 in cell H7. In the Solver window this constraint is entered as it originally was, H7 <= J7 . The fourth guideline constraint could be entered in its original form similarly.

[Page 123]

Solution Analysis

The solution is

x ₃ = $38,181.82 invested in treasury bonds

x ₄ = $31,818.18 invested in a growth stock fund

Z = $6,818.18

The sensitivity report for our Excel spreadsheet solution to this problem is shown in Exhibit 4.9.

Exhibit 4.9.

Notice that the dual (shadow price) value for constraint 5 (i.e., the sum of the investments must equal $70,000) is 0.095. This indicates that for each additional $1 Kathleen Allen invests (above $70,000), according to the existing investment guidelines she has established, she could expect a return of 9.5%. The sensitivity ranges show that there is no upper bound on the amount she could invest and still receive this return.

An interesting variation of the problem is to not specify that the entire amount available (in this case, $70,000) must be invested. This changes the constraints for the first and third guidelines and the constraint that requires that the entire $70,000 be invested.

Recall that the first guideline is "no more than 20% of the total investment should be in municipal bonds." The total investment is no longer exactly $70,000, but the sum of all four investments, x ₁ + x ₂ + x ₃ + x ₄ . The constraint showing that the amount invested in municipal bonds, x ₁ , as a percentage (or ratio) of this total cannot exceed 20% is written as

Rewriting this constraint in a form more consistent with a linear programming solution (to eliminate the fractional relationship between variables) results in

x ₁ 0.2( x ₁ + x ₂ + x ₃ + x ₄ )

[Page 124]

and

0.8 x ₁ 0.2 x ₂ 0.2 x ₃ 0.2 x ₄

Management Science Application: A Linear Programming Model for Optimal Portfolio Selection at Prudential Securities, Inc

In the secondary mortgage market, government agencies purchase mortgage loans from the original mortgage lenders and pool them to create mortgage- backed securities (MBSs). These securities are traded in capital markets along with other fixed-income securities, such as treasury and corporate bonds. The total size of this market for MBSs is well over $1 trillion. There are a number of types of MBSs. The market for MBSs is maintained by a network of dealers, including Prudential Securities, Inc. This firm and others like it underwrite and issue new market-based securities. This market is somewhat more complex than standard bond investments, such as treasury or corporate securities, because the principal on mortgages is returned gradually over the life of the security rather than in a lump sum at the end. In addition, cash flows fluctuate because of the homeowner 's right to prepay mortgages. In order to deal with these complexities, Prudential Securities has developed and implemented a number of management science models to reduce investment risk and properly value securities for its investors. One such model employs linear programming to design an optimal securities portfolio to meet various investors' criteria under different interest rate environments. The linear programming model determines the amount to invest in different MBSs to meet a client's objectives for portfolio performance. Constraints might include maximum and minimum percentages (of the total portfolio investment) that could be invested in any one or more securities, the duration of the securities, the amount to be invested, and the amount of the different securities available. This linear programming model and other management science models are used hundreds of times each day at Prudential Securities by traders, salespeople, and clients . The models allow the firm to participate successfully in the mortgage market. Prudential's secondary market trading in MBSs typically exceeds $5 billion per week.

Source: Y. Ben-Dow, L. Hayre, and V. Pica, "Mortgage Valuation Models at Prudential Securities," Interfaces 22, no. 1 (JanuaryFebruary 1992): 5571.

The constraint for the third guideline, which stipulates that at least 30% of the total investment ( x ₁ + x ₂ + x ₃ + x ₄ ) should be in treasury bills and CDs ( x ₂ + x ₃ ), is formulated similarly as

and

-0.3 x ₁ + 0.7 x ₂ + 0.7 x ₃ 0.3 x ₄

Because the entire $70,000 does not have to be invested, the last constraint becomes

x ₁ + x ₂ + x ₃ + x ₄ 70,000

The complete linear programming model is summarized as

[Page 125]

The solution to this altered model is exactly the same as the solution to our original model, wherein the entire $70,000 must be invested. This is logical because only positive returns are achieved from investing, and thus the investor would leave no money not invested. However, if losses could be realized from some investments, then it might be a good idea to construct the model so that the entire amount would not have to be invested.