Section 2.1. Symmetric Cipher Model

[Page 30 (continued)]

2.1. Symmetric Cipher Model

A symmetric encryption scheme has five ingredients (Figure 2.1):

Plaintext: This is the original intelligible message or data that is fed into the algorithm as input.
Encryption algorithm: The encryption algorithm performs various substitutions and transformations on the plaintext.
Secret key: The secret key is also input to the encryption algorithm. The key is a value independent of the plaintext and of the algorithm. The algorithm will produce a different output depending on the specific key being used at the time. The exact substitutions and transformations performed by the algorithm depend on the key.
Ciphertext: This is the scrambled message produced as output. It depends on the plaintext and the secret key. For a given message, two different keys will produce two different ciphertexts. The ciphertext is an apparently random stream of data and, as it stands, is unintelligible.
Decryption algorithm: This is essentially the encryption algorithm run in reverse. It takes the ciphertext and the secret key and produces the original plaintext.

Figure 2.1. Simplified Model of Conventional Encryption

There are two requirements for secure use of conventional encryption:

We need a strong encryption algorithm. At a minimum, we would like the algorithm to be such that an opponent who knows the algorithm and has access to one or more ciphertexts would be unable to decipher the ciphertext or figure out the key. This requirement is usually stated in a stronger form: The opponent should be unable to decrypt ciphertext or discover the key even if he or she is in possession of a number of ciphertexts together with the plaintext that produced each ciphertext.
[Page 31]
Sender and receiver must have obtained copies of the secret key in a secure fashion and must keep the key secure. If someone can discover the key and knows the algorithm, all communication using this key is readable.

We assume that it is impractical to decrypt a message on the basis of the ciphertext plus knowledge of the encryption/decryption algorithm. In other words, we do not need to keep the algorithm secret; we need to keep only the key secret. This feature of symmetric encryption is what makes it feasible for widespread use. The fact that the algorithm need not be kept secret means that manufacturers can and have developed low-cost chip implementations of data encryption algorithms. These chips are widely available and incorporated into a number of products. With the use of symmetric encryption, the principal security problem is maintaining the secrecy of the key.

Let us take a closer look at the essential elements of a symmetric encryption scheme, using Figure 2.2. A source produces a message in plaintext, X = [X₁, X₂, ..., X_M]. The M elements of X are letters in some finite alphabet. Traditionally, the alphabet usually consisted of the 26 capital letters. Nowadays, the binary alphabet {0, 1} is typically used. For encryption, a key of the form K = [K₁, K₂, ..., K_J] is generated. If the key is generated at the message source, then it must also be provided to the destination by means of some secure channel. Alternatively, a third party could generate the key and securely deliver it to both source and destination.

Figure 2.2. Model of Conventional Cryptosystem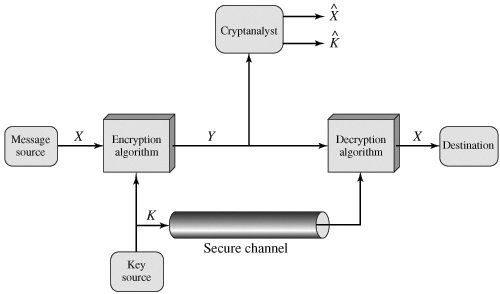

With the message X and the encryption key K as input, the encryption algorithm forms the ciphertext Y = [Y₁, Y₂, ..., Y_N]. We can write this as

Y = E(K, X)

[Page 32]

This notation indicates that Y is produced by using encryption algorithm E as a function of the plaintext X, with the specific function determined by the value of the key K.

The intended receiver, in possession of the key, is able to invert the transformation:

X = D(K, Y)

An opponent, observing Y but not having access to K or X, may attempt to recover X or K or both X and K. It is assumed that the opponent knows the encryption (E) and decryption (D) algorithms. If the opponent is interested in only this particular message, then the focus of the effort is to recover X by generating a plaintext estimate . Often, however, the opponent is interested in being able to read future messages as well, in which case an attempt is made to recover K by generating an estimate .

Cryptography

Cryptographic systems are characterized along three independent dimensions:

The type of operations used for transforming plaintext to ciphertext. All encryption algorithms are based on two general principles: substitution, in which each element in the plaintext (bit, letter, group of bits or letters) is mapped into another element, and transposition, in which elements in the plaintext are rearranged. The fundamental requirement is that no information be lost (that is, that all operations are reversible). Most systems, referred to as product systems, involve multiple stages of substitutions and transpositions.
The number of keys used. If both sender and receiver use the same key, the system is referred to as symmetric, single-key, secret-key, or conventional encryption. If the sender and receiver use different keys, the system is referred to as asymmetric, two-key, or public-key encryption.
The way in which the plaintext is processed. A block cipher processes the input one block of elements at a time, producing an output block for each input block. A stream cipher processes the input elements continuously, producing output one element at a time, as it goes along.

Cryptanalysis

Typically, the objective of attacking an encryption system is to recover the key in use rather then simply to recover the plaintext of a single ciphertext. There are two general approaches to attacking a conventional encryption scheme:

Cryptanalysis: Cryptanalytic attacks rely on the nature of the algorithm plus perhaps some knowledge of the general characteristics of the plaintext or even some sample plaintext-ciphertext pairs. This type of attack exploits the characteristics of the algorithm to attempt to deduce a specific plaintext or to deduce the key being used.

[Page 33]

Brute-force attack: The attacker tries every possible key on a piece of ciphertext until an intelligible translation into plaintext is obtained. On average, half of all possible keys must be tried to achieve success.

If either type of attack succeeds in deducing the key, the effect is catastrophic: All future and past messages encrypted with that key are compromised.

We first consider cryptanalysis and then discuss brute-force attacks.

Table 2.1 summarizes the various types of cryptanalytic attacks, based on the amount of information known to the cryptanalyst. The most difficult problem is presented when all that is available is the ciphertext only. In some cases, not even the encryption algorithm is known, but in general we can assume that the opponent does know the algorithm used for encryption. One possible attack under these circumstances is the brute-force approach of trying all possible keys. If the key space is very large, this becomes impractical. Thus, the opponent must rely on an analysis of the ciphertext itself, generally applying various statistical tests to it. To use this approach, the opponent must have some general idea of the type of plaintext that is concealed, such as English or French text, an EXE file, a Java source listing, an accounting file, and so on.

Table 2.1. Types of Attacks on Encrypted Messages
Type of Attack	Known to Cryptanalyst
Ciphertext only	Encryption algorithm Ciphertext
Known plaintext	Encryption algorithm Ciphertext One or more plaintext-ciphertext pairs formed with the secret key
Chosen plaintext	Encryption algorithm Ciphertext Plaintext message chosen by cryptanalyst, together with its corresponding ciphertext generated with the secret key
Chosen ciphertext	Encryption algorithm Ciphertext Purported ciphertext chosen by cryptanalyst, together with its corresponding decrypted plaintext generated with the secret key
Chosen text	Encryption algorithm Ciphertext Plaintext message chosen by cryptanalyst, together with its corresponding ciphertext generated with the secret key Purported ciphertext chosen by cryptanalyst, together with its corresponding decrypted plaintext generated with the secret key

The ciphertext-only attack is the easiest to defend against because the opponent has the least amount of information to work with. In many cases, however, the analyst has more information. The analyst may be able to capture one or more plaintext messages as well as their encryptions. Or the analyst may know that certain plaintext patterns will appear in a message. For example, a file that is encoded in the Postscript format always begins with the same pattern, or there may be a standardized header or banner to an electronic funds transfer message, and so on. All these are examples of known plaintext. With this knowledge, the analyst may be able to deduce the key on the basis of the way in which the known plaintext is transformed.

[Page 34]

Closely related to the known-plaintext attack is what might be referred to as a probable-word attack. If the opponent is working with the encryption of some general prose message, he or she may have little knowledge of what is in the message. However, if the opponent is after some very specific information, then parts of the message may be known. For example, if an entire accounting file is being transmitted, the opponent may know the placement of certain key words in the header of the file. As another example, the source code for a program developed by Corporation X might include a copyright statement in some standardized position.

If the analyst is able somehow to get the source system to insert into the system a message chosen by the analyst, then a chosen-plaintext attack is possible. An example of this strategy is differential cryptanalysis, explored in Chapter 3. In general, if the analyst is able to choose the messages to encrypt, the analyst may deliberately pick patterns that can be expected to reveal the structure of the key.

Table 2.1 lists two other types of attack: chosen ciphertext and chosen text. These are less commonly employed as cryptanalytic techniques but are nevertheless possible avenues of attack.

Only relatively weak algorithms fail to withstand a ciphertext-only attack. Generally, an encryption algorithm is designed to withstand a known-plaintext attack.

Two more definitions are worthy of note. An encryption scheme is unconditionally secure if the ciphertext generated by the scheme does not contain enough information to determine uniquely the corresponding plaintext, no matter how much ciphertext is available. That is, no matter how much time an opponent has, it is impossible for him or her to decrypt the ciphertext, simply because the required information is not there. With the exception of a scheme known as the one-time pad (described later in this chapter), there is no encryption algorithm that is unconditionally secure. Therefore, all that the users of an encryption algorithm can strive for is an algorithm that meets one or both of the following criteria:

The cost of breaking the cipher exceeds the value of the encrypted information.
The time required to break the cipher exceeds the useful lifetime of the information.

An encryption scheme is said to be computationally secure if either of the foregoing two criteria are met. The rub is that it is very difficult to estimate the amount of effort required to cryptanalyze ciphertext successfully.

All forms of cryptanalysis for symmetric encryption schemes are designed to exploit the fact that traces of structure or pattern in the plaintext may survive encryption and be discernible in the ciphertext. This will become clear as we examine various symmetric encryption schemes in this chapter. We will see in Part Two that cryptanalysis for public-key schemes proceeds from a fundamentally different premise, namely, that the mathematical properties of the pair of keys may make it possible for one of the two keys to be deduced from the other.

[Page 35]

A brute-force attack involves trying every possible key until an intelligible translation of the ciphertext into plaintext is obtained. On average, half of all possible keys must be tried to achieve success. Table 2.2 shows how much time is involved for various key spaces. Results are shown for four binary key sizes. The 56-bit key size is used with the DES (Data Encryption Standard) algorithm, and the 168-bit key size is used for triple DES. The minimum key size specified for AES (Advanced Encryption Standard) is 128 bits. Results are also shown for what are called substitution codes that use a 26-character key (discussed later), in which all possible permutations of the 26 characters serve as keys. For each key size, the results are shown assuming that it takes 1 ms to perform a single decryption, which is a reasonable order of magnitude for today's machines. With the use of massively parallel organizations of microprocessors, it may be possible to achieve processing rates many orders of magnitude greater. The final column of Table 2.2 considers the results for a system that can process 1 million keys per microsecond. As you can see, at this performance level, DES can no longer be considered computationally secure.

Table 2.2. Average Time Required for Exhaustive Key Search
Key size (bits)	Number of alternative keys		Time required at 1 decryption/ms		Time required at 10⁶ decryption/ms
32	2³²	= 4.3 x 10⁹	2³¹ ms	= 35.8 minutes	2.15 milliseconds
56	2⁵⁶	= 7.2 x 10¹⁶	2⁵⁵ ms	= 1142 years	10.01 hours
128	2¹²⁸	= 3.4 x 10³⁸	2¹²⁷ ms	= 5.4 x 10²⁴ years	5.4 x 10¹⁸ years
168	2¹⁶⁸	= 3.7 x 10⁵⁰	2¹⁶⁷ ms	= 5.9 x 10³⁶ years	5.9 x 10³⁰ years
26 characters (permutation)	26!	= 4 x 10²⁶	2 x 10²⁶ ms	= 6.4 x 10¹² years	6.4 x 10⁶ years

2.1. Symmetric Cipher Model

Figure 2.1. Simplified Model of Conventional Encryption

Figure 2.2. Model of Conventional Cryptosystem

Cryptography

Cryptanalysis

Table 2.1. Types of Attacks on Encrypted Messages

Table 2.2. Average Time Required for Exhaustive Key Search