| When customers in a queuing network model exhibit different routing patterns, different service time requirements, and/or different scheduling disciplines, the model is said to have multiple classes of customers. Consider a local area network with P client workstations and Q servers. Each client workstation may have its own local storage, but it may also require additional storage capacity from the servers. After executing at a workstation, a process sends a request across the network to acquire service from one of the storage servers. Each client workstation process places one request at a time on the network. A queuing model of this system is proposed in [22]. If all client processes have identical workload requirements and balance their service requests across all file servers, the system can be modeled by a single-class workload with P processes. However, if each client process restricts its requests to a subset of servers, with each client visiting a different set of servers, performance can be significantly improved. By judiciously segregating clients on the servers, potential queuing delays are reduced and average response time is likewise reduced. In this alternative model, each client process has a different routing probability (i.e., each process visits a different set of servers) and a separate workload class is required to represent each client workstation. Thus the system is modeled with P classes, each with exactly one process in each class. In general, the queuing networks considered here consist of K devices (or service centers) and R different classes of customers. A central concept in the analysis and solution of queuing networks is the state of the network. The state represents a distribution of customers over classes and devices. The network state is denoted by a vector 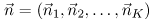 , where component , where component 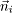 (i = 1, ..., K) is a vector that represents the number of customers of each class at server i. That is, (i = 1, ..., K) is a vector that represents the number of customers of each class at server i. That is, 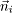 = (ni,1, ni,2,....,ni,R) where ni,r represents the number of class r customers at server i. For instance, returning to the example in Figure 13.1 the state of the system is defined as ( = (ni,1, ni,2,....,ni,R) where ni,r represents the number of class r customers at server i. For instance, returning to the example in Figure 13.1 the state of the system is defined as (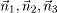 ), where ), where 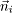 is a tuple specifying the number of update and query transactions at device i. Two possible states in this example include ((1,3),(0,0),(0,0)) and ((0,1),(0,2),(1,0)). The former state indicates that all transactions (i.e., one update and three query transactions) are at the processor. The latter state represents the situation where one query transaction is executing at the processor, two queries are at disk 1, and the update transaction is being serviced at disk 2. is a tuple specifying the number of update and query transactions at device i. Two possible states in this example include ((1,3),(0,0),(0,0)) and ((0,1),(0,2),(1,0)). The former state indicates that all transactions (i.e., one update and three query transactions) are at the processor. The latter state represents the situation where one query transaction is executing at the processor, two queries are at disk 1, and the update transaction is being serviced at disk 2. The BCMP theorem [3], developed by Baskett, Chandy, Muntz, and Palacios, specifies a combination of service time distributions and scheduling disciplines that yield multiclass product-form queuing networks that lend themselves to efficient model solution techniques. Open, closed, or mixed networks are allowed. A closed network consists of only closed classes with a constant number of customers in each class at all times. In contrast, an open network allows customers in each class to enter or leave the network. A mixed network is closed with respect to some classes and open with respect to other classes. Basically, the set of assumptions required by the BCMP theorem for a product-form solution is as follows. Service centers with a FCFS discipline. In this case, customers are serviced in the order in which they arrive. The service time distributions are required to be exponential with the same mean for all classes. Although all classes must have the same mean service time at any given device, they may have different visit ratios, which allows the possibility of different service demands for each class at any given device. The service rate is allowed to be load dependent, but it can be dependent only on the total number of customers at the server and not on the number of customers of any particular class. For instance, requests from clients to a file server can be normally modeled by a FCFS load-independent server. Disks are usually modeled as FCFS service centers, with load-dependent service rates to represent reduced service times as the load at the disk increases (i.e., effectively modeling shortest seek time first or SCAN scheduling policies). Service centers with a PS discipline. When there are n customers at a server with a processor sharing (PS) discipline, each customer receives service at a rate of 1/n of their normal service rate. Each class may have a distinct service time distribution. The round robin (RR) scheduling discipline allows customers to receive a fixed quantum of service. If the customer does not finish execution within its allocated quantum, it returns to the end of the queue, awaiting further service. In the limiting case, when the quantum approaches zero, the RR discipline becomes the PS discipline. Operating systems normally employ the RR discipline. Thus PS is a reasonable approximation to represent processor scheduling disciplines of modern operating systems. Service centers with infinite servers (IS). When there is an infinite supply of servers in a service center, there is never any waiting for a server. This situation is known as IS, delay server, or no queuing. For instance, think time at terminals in an interactive system is usually modeled by delay servers. In a lightly loaded LAN, the time needed to send a request from a client workstation to a server can also be approximated by a delay server. Basically, any component of a system where there is a constant delay that is independent of the overall load (i.e., arrive rate, multiprogramming level) can be modeling by an IS server. Service centers with a LCFS-PR discipline. Under last-come-first-served-preemptive-resume (LCFS-PR), whenever a new customer arrives, the server preempts servicing the previous customer (if any) and is allocated to the newly arriving customer. When a customer completes, the server resumes executing its previously preempted job. Each class may have a distinct service time distribution. High priority interrupts that require immediate but small amounts of service are adequately modeled by LCFS-PR servers.
In open networks, the time between successive arrivals is assumed to be exponentially distributed. Bulk arrivals are not allowed. Multi-class product-form networks have efficient computational algorithms for their solution. The two major algorithms are convolution [6] and MVA [16]. Because of their simplicity and intuitive appeal, this chapter presents MVA-based algorithms for exact and approximate solutions of models with multiple classes. (Also see [13] for MVA-based algorithms of QNs and [8] for solution algorithms based on decomposition and aggregation techniques.) The following notation is used for the multiclass models presented here. K: number of devices or service centers of the model R: number of classes of customers Mr: number of terminals of class r Zr: think time of class r Nr: class r population lr: arrival rate of class r Si,r: average service time of class r customers at device i
Vi,r: average visit ratio of class r customers at device i Di,r: average service demand of class r customers at device i; Di,r = Vi,r Si,r: Ri,r: average response time per visit of class r customers at device i R'i,r: average residence time of class r customers at device i (i.e., the total time spent by class r customers at device i over all visits to the device); 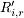 ñi,r: average number of class r customers at device i ñi: average number of customers at device i Xi,r: class r throughput at device i X0,r: class r system throughput Rr: class r response time
|