Binary Numbers, Bits, and Bytes | C Primer Plus (5th Edition)

I l @ ve RuBoard

Binary Numbers , Bits, and Bytes

The usual way to write numbers is based on the number 10. For instance, 2,157 has a 2 in the thousands place, a 1 in the hundreds place, a 5 in the tens place, and a 7 in the ones place. This means you can think of 2,157 as being the following:

 2 x 1000 + 1 x 100 + 5 x 10 + 7 x 1

However, 1,000 is 10 cubed, 100 is 10 squared, 10 is 10 to the first power, and, by convention, 1 is 10 (or any positive number) to the zero power. Therefore, you can also write 2,157 as this:

 2 x 10 ³ + 1 x 10 ² + 5 x 10 ¹ + 7 x 10

Because our system of writing numbers is based on powers of ten, we say that 2,157 is written in base 10 .

Presumably, the decimal system evolved because we have ten fingers. A computer bit, in a sense, has only two fingers because it can be set only to 0 or 1, off or on. Therefore, a base 2 system is natural for a computer. It uses powers of two instead of powers of ten. Numbers expressed in base 2 are termed binary numbers. The number 2 plays the same role for binary numbers that the number 10 does for base 10 numbers. For example, a binary number such as 1,101 mean this:

 1 x 2 ³ + 1 x 2 ² + 0 x 2 ¹ + 1 x 2

In decimal numbers, it becomes this:

 1 x 8 + 1 x 4 + 0 x 2 + 1 x 1 = 13

You can use the binary system to express any number (if you have enough bits) as a combination of 1s and 0s. This system is very convenient for digital computers, which express information in combinations of on and off states that can be interpreted as 1s and 0s. Let's see how the binary system works for a 1-byte integer.

Binary Integers

Usually, a byte contains 8 bits. C, remember, uses the term byte to denote the size used to hold a system's character set, so a C byte could be 8 bits, 9 bits, 16 bits, or some other value. However, the 8-bit byte is the byte used to describe memory chips and the byte used to describe data transfer rates. To keep matters simple, this chapter assumes an 8-bit byte. You can think of these 8 bits as being numbered from 7 to 0, left to right. Bit 7 is called the high-order bit , and bit 0 is the low-order bit in the byte. Each bit number corresponds to a particular exponent of 2. Imagine the byte as looking like Figure 15.1.

Figure 15.1. Bit numbers and bit values.

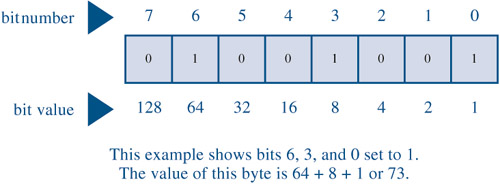
Here, 128 is 2 to the 7th power, and so on. The largest number this byte can hold is 1, with all bits set to 1: 11111111. The value of this binary number is as follows :

 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255

The smallest binary number would be 00000000, or a simple 0. A byte can store numbers from 0 to 255, for a total of 256 possible values. By changing the interpretation, a byte can store numbers from -128 to +127, again a total of 256 values.

Signed Integers

The representation of signed numbers is determined by the hardware, not by C. Probably the simplest way to represent signed numbers is to reserve 1 bit, such as the high-order bit, to represent the sign. In a 1-byte value, this leaves 7 bits for the number itself. In such a sign-magnitude representation, 10000001 is -1 and 00000001 is 1. The total range, then, is -127 to +127.

One disadvantage of this approach is that it has two zeros: +0 and -0. This is confusing, and it also uses up two bit patterns for just one value.

The two's-complement method avoids that problem and is the most common system used today. We'll discuss this method as it applies to a 1-byte value. In that context, the values 0 through 127 are represented by the last 7 bits, with the high-order bit set to 0. So far, that's the same as the sign-magnitude method. Also, if the high-order bit is 1, the value is negative. The difference comes in determining the value of that negative number. Subtract the bit-pattern for a negative number from the 9-bit pattern 100000000 (256 expressed in binary), and the result is the magnitude of value. For example, suppose the pattern is 10000000. As an unsigned byte, it would be 128. As a signed value, it is negative (bit 7 is 1) and has a value of 100000000 - 10000000, or 10000000 (128). Therefore, the number is -128. (It would have been -0 in the sign-magnitude system.) Similarly, 10000001 is -127, and 11111111 is -1. The method represents numbers in the range -128 to +127.

The simplest method for reversing the sign of a two's-complement binary number is to invert each bit (convert 0s to 1s and 1s to 0s) and then add 1. Because 1 is 00000001, -1 is 11111110 + 1, or 11111111, just as you saw earlier.

The one's-complement method forms the negative of a number by inverting each bit in the pattern. For instance, 00000001 is 1 and 11111110 is -1. This method also has a -0: 11111111. Its range (for a 1-byte value) is -127 to +127.

Binary Floating Point

Floating-point numbers are stored in two parts : a binary fraction and a binary exponent. Let's see how this is done.

Binary Fractions

The ordinary fraction 0.527 represents

 5/10 + 2/100 + 7/1000

with the denominators representing increasing powers of ten. In a binary fraction, you use powers of two for denominators, so the binary fraction .101 represents

 1/2 + 0/4 + 1/8

which in decimal notation is

 0.50 + 0.00 + 0.125

or 0.625.

Many fractions, such as 1/3, cannot be represented exactly in decimal notation. Similarly, many fractions cannot be represented exactly in binary notation. Indeed, the only fractions that can be represented exactly are combinations of multiples of powers of 1/2. Therefore, 3/4 and 7/8 can be represented exactly as binary fractions, but 1/3 and 2/5 cannot be.

Floating-Point Representation

To represent a floating-point number in a computer, a certain number of bits (depending on the system) are set aside to hold a binary fraction. Additional bits hold an exponent. In general terms, the actual value of the number consists of the binary fraction times 2 to the indicated exponent. Multiplying a floating-point number by, say, 4, increases the exponent by 2 and leaves the binary fraction unchanged. Multiplying by a number that is not a power of 2 changes the binary fraction and, if necessary, the exponent.

I l @ ve RuBoard