30.3 Properties

< Free Open Study >

We now turn to establishing the basic properties of F_ω—in particular the usual preservation and progress theorems. The ideas behind these proofs are similar to what we've seen before, but we need to proceed carefully because we are now dealing with a somewhat larger and more complicated system. In particular, it will require some work to analyze the structure of the type equivalence relation. To shorten the proofs, we treat only the universal part of F_ω, the system defined in Figure 30-1. Extending the arguments to cover existential types is straightforward.

Basic Properties

We begin with some simple properties that will be needed later.

30.3.1 Lemma [Strengthening]

If Г, x:S, Δ ⊢ T :: K, then Г, Δ ⊢ T :: K.

Proof: The kinding relation does not refer to term variable bindings.

For the sake of variety, let us prove permutation and weakening for F_ω together, rather than one after the other as we have done previously.

30.3.2 Lemma [Permutation and Weakening]

Suppose we have contexts Г and Δ such that Δ is a well-formed permutation of Г, Σ for some context Σ—that is, Δ is a permutation of an extension of Г.

If Г ⊢ T :: K, then Δ ⊢ T :: K.
If Г ⊢ t : T, then Δ ⊢ t : T.

Proof: Straightforward induction on derivations.

30.3.3 Lemma [Term Substitution]

If Г, x:S, Δ ⊢ t : T and Г ⊢ s : S, then Г, Δ ⊢ [x ↦ s]t : T.

Proof: By induction on derivations. (EXERCISE [⋆]: Where is Lemma 30.3.1 used? What about Lemma 30.3.2?)

30.3.4 Lemma [Type Substitution]

If Г, Y::J, Δ ⊢ T :: K and Г ⊢ S :: J, then Г, [Y ↦ S]Δ ⊢ [Y ↦ S]T :: K.
If T ≡ U, then [Y ↦ S]T ≡ [Y ↦ S]U.
If Г, Y::J, Δ ⊢ t : T and Г ⊢ S :: J, then Г, [Y ↦ S]Δ ⊢ [Y ↦ S]t : [Y ↦ S]T.

Proof: Straightforward induction on derivations, using weakening (Lemma 30.3.2) for the K-TVAR, and T-VAR cases. For the Q-APPABS case, we also need the observation that [X ↦ [Y ↦ S]T₂]([Y ↦ S]T₁₂) is the same thing as [Y ↦ S]([X ↦ T₂]T₁₂).

Type Equivalence and Reduction

For establishing the properties of typing in F_ω, it is convenient to use a directed variant of the type equivalence relation, called parallel reduction (see Figure 30-3). The differences from type equivalence are that the rules of symmetry and transitivity are dropped, and that the QR-APPABS rule allows reductions in the subphrases of the redex. Dropping symmetry gives the reduction relation a more "computational" feel, with (λX::K₁₁.T₁₂)T₂ reducing to [X ↦ T₂]T₁₂, but not the other way around; this directedness makes the relation easier to analyze, e.g., in the proof of Lemma 30.3.12 below. Dropping transitivity and allowing reduction of the components at the same time as reducing a lambda-redex are technicalities: we make these changes to obtain a relation with the single-step diamond property stated in Lemma 30.3.8 below.

Figure 30-3: Parallel reduction on types

A key property of the parallel reduction relation is that its transitive and symmetric closure, written , coincides with type equivalence.

30.3.5 Lemma

S ≡ T iff .

Proof: The (⇐) direction is obvious. For the (⇛) direction, the only difficulty is the fact that a type equivalence derivation may use instances of Q-SYMM and Q-TRANS at arbitrary points, while the definition of the relation permits uses of symmetry and transitivity only at the outermost level. This can be dealt with by observing that any derivation of S ≡ T can be transformed into a chain of transitivity-free derivations S = S₀ ≡ S₁ ≡ S₂ ≡ ... ≡ S_n = T glued together with transitivity at the top, where, in each subderivation S_i ≡ S_i+1 Q-SYMM is used only as the final rule (or not at all).

Moreover, parallel reduction is easily seen to be confluent, as the next few lemmas show. (Confluence is often called the Church-Rosser property.)

30.3.6 Lemma

If S ⇛ S′, then [Y ↦ S]T ⇛ [Y ↦ S′]T for any type T.

Proof: By induction on the structure of T.

30.3.7 Lemma

If S ⇛ S′ and T ⇛ T′, then [Y ↦ S]T ⇛ [Y ↦ S′]T′.

Proof: By induction on the second given derivation. The QR-REFL case uses Lemma 30.3.6. The cases for QR-ABS, QR-APP, QR-ARROW, and QR-ALL proceed by straightforward use of the induction hypothesis. In QR-APPABS case, we have T = (λX::K₁₁.T₁₂) T₂ and , with and . By the induction hypothesis, and . Applying QR-APPABS, we obtain , i.e., .

30.3.8 Lemma [Single-Step Diamond Property of Reduction]

If S ⇛ T and S ⇛ U, then there is some type V such that T ⇛ V and U ⇛ V.

Proof: Exercise [Recommended, ⋆⋆⋆].

30.3.9 Lemma [Confluence]

If S ⇛* T and S ⇛* U, then there is some type V such that T ⇛* V and U ⇛* V.

Proof: If we visualize the individual steps of reduction from S to T and from S to U like this,

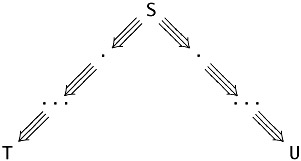
then we can repeatedly use Lemma 30.3.8 to tile the interior of the diagram

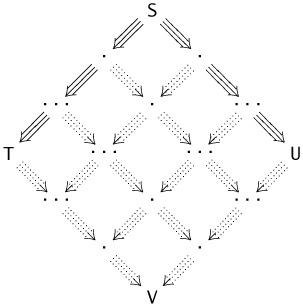
to obtain a large diamond. The lower edges of this diamond are the required reductions.

30.3.10 Proposition

If , then there is some U such that S ⇛* U and T ⇛* U.

Proof: Exercise [⋆⋆].

This brings us to the crucial observation relating equivalence and reduction: if two types are equivalent, then they share a common reduct. This gives us the structure we need to prove the inversion properties that follow.

30.3.11 Corollary

If S ≡ T, then there is some U such that S ⇛* U and T ⇛* U.

Preservation

We are now almost ready for the main proof that types are preserved during reduction. The only other thing we need is, as usual, an inversion lemma that, given a typing derivation whose conclusion has a certain shape, tells us about the shape of its subderivations. This lemma, in turn, depends on a simple observation about parallel reduction.

30.3.12 Lemma [Preservation of Shapes Under Reduction]

If S₁→S₂ ⇛* T, then T = T₁→T₂ with S₁⇛* T₁ and S₂ ⇛* T₂.
If "X::K₁.S₂ ⇛* T, then T = "X::K₁.T₂ with S₂⇛* T₂.

Proof: Straightforward induction.

30.3.13 Lemma [Inversion]

If Г ⊢ λx:S₁. s₂ : T₁→T₂, then T₁ ≡ S₁ and Г, x:S₁ ⊢ s₂ : T₂. Also, Г ⊢ S₁ :: *.
If Г ⊢ λX::J₁ . s₂ : "X::K₁ . T₂, then J₁ = K₁ and Г, X::J₁ ⊢ s₂ : T₂.

Proof: For part 1, we prove, by induction, the following slightly more general statement: If Г ⊢ λx:S₁.s₂ : S and S ≡ T₁→T₂, then T₁ ≡ S₁ and Г, x:S₁ ⊢ s₂ : T₂. The induction step, rule T-EQ is straightforward. The interesting case is the base of the induction, rule T-ABS. In this case, S has the form S₁→S₂, where Г, x:S₁ ⊢ s₂ : S₂. Lemma 30.3.12(1) gives us T₁ ≡ S₁ and T₂ ≡ S₂, from which T-EQ gives Г, x:S₁ ⊢ s₂ : T₂. Moreover, the other premise of T-ABS gives us Г ⊢ S₁ :: *. Part 2 is similar.

30.3.14 Theorem [Preservation]

If Г ⊢ t : T and t → t′, then Г ⊢ t′ : T.

Proof: Straightforward induction on typing derivations. The argument is similar to the proof of preservation for the simply typed lambda-calculus with subtyping (15.3.5).

Case T-VAR:

t = x

Can't happen (there are no evaluation rules for variables).

Case T-ABS:

t = λx:T₁. t₂

Can't happen (t is already a value).

Case T-APP:

t = t₁ t₂

Г ⊢ t₁ : T₁₁→T₁₂

Г ⊢ t₂ : T₁₁

T = T₁₂

From Figure 30-1, we see that there are three rules by which t → t′ can be derived: E-APP1, E-APP2, and E-APPABS. For the first two, the result follows by straightforward use of the induction hypothesis. The third is more interesting:

Subcase E-APPABS:

t₁ = λx:S₁₁. t₁₂

t₂ = v₂

t′ = [x ↦ v₂]t₁₂

By Lemma 30.3.13(1), T₁₁ ≡ = S₁₁ and Г, x:S₁₁ ⊢ t₁₂ : T₁₂. By T-EQ, Г ⊢ t₂ : S₁₁. From this and the substitution lemma (30.3.3), we obtain Г ⊢ t′ : T₁₂.

Case T-TABS:

t = λX::K₁ .t₂

Can't happen (t is already a value).

Case T-TAPP:

 t = t₁ [T₂]    Г ⊢ t₁ : "X::K₁₁ . T₁₂    Г ⊢ T₂ :: K₁₁ T = [X ↦ T₂]T₁₂

Similar to the T-APP case, using the type substitution lemma (30.3.4) in place of the term substitution lemma (30.3.3).

Case T-EQ:

Г ⊢ t : S

S ≡ T

Г ⊢ T ::*

By the induction hypothesis, Г ⊢ t′ : S. By T-EQ, Г ⊢ t′ : T.

Progress

Our next task is the progress theorem. Again, we already have most of what we need for the proof—all that remains is a standard canonical forms lemma that tells us about the shapes of closed values.

30.3.15 Lemma [Canonical Forms]

If t is a closed value with ⊢ t : T₁→T₂, then t is an abstraction.
If t is a closed value with ⊢ t : "X::K₁.T₂, then t is a type abstraction.

Proof: The arguments for the two parts are similar; we show just (1). Since there are only two forms of values, if t is a value and not an abstraction, then it must be a type abstraction. So suppose (for a contradiction) that it is a type abstraction. Then the given typing derivation for ⊢ t : T₁→T₂ must end with a use of T-TABS followed by a nonempty sequence of uses of T-EQ. That is, it must have the following form (eliding kinding premises):

Since type equivalence is transitive, we can collapse all of these uses of equivalence into one and conclude that "X::K₁₁.S₁₂ ≡ T₁→T₂. Now, by Proposition 30.3.11, there must be some type U such that "X::K₁₁.S₁₂ ⇛* U and T₁→T₂⇛* U. By Lemma 30.3.12, such a U must have both a quantifier and an arrow as its outermost constructor, a contradiction.

30.3.16 Theorem [Progress]

Suppose t is a closed, well-typed term (that is, ⊢ t : T for some T). Then either t is a value or else there is some t′ with t → t′.

Proof: By induction on typing derivations. The T-VAR case cannot occur, because t is closed. The T-ABS and T-TABS cases are immediate, since abstractions are values. The T-EQ case follows directly from the induction hypothesis. The remaining cases, for application and type application, are more interesting. We give just the case for type application; the other is similar.

Case T-TAPP:

t = t₁ [T₂]

⊢ t₁ : "X::K₁₁.T₁₂

⊢ T₂ :: K₁₁

By the induction hypothesis, either t₁ is a value or else it can make a step of evaluation. If t₁ can take a step, then rule E-TAPP applies to t. If t₁ is a value, then the canonical forms lemma (30.3.15) tells us that t₁ is a type abstraction, so rule E-TAPPTABS applies to t.

30.3.17 Exercise [Recommended, ⋆⋆]

Suppose we add to the type equivalence relation the following peculiar rule:

                                T→T ≡ "X::*.T

Which, if any, of the basic properties of the system would fail? On the other hand, suppose that we add this rule:

                                  S→T ≡ T→S

Now which properties fail, if any?

Kinding

In the definition of F_ω in Figure 30-1 we took some pains to ensure the well-kindedness of the types we can derive for terms using the rules. In particular, T-ABS checks that the type annotation on a lambda-abstraction is well formed before adding it to the context, and T-EQ checks that the type T being attributed to t has kind *. The precise sense in which these checks ensure well-formedness is given by the following proposition.

30.3.18 Definition

A context Г is said to be well formed if (1) Г is empty, or (2) Г = Г₁, x:T with Г₁ well formed and Г ⊢ T :: *, or (3) Г = Г₁, X::K with Г₁ well formed.

30.3.19 Proposition

If Г ⊢ t : T and Г is well formed, then Г ⊢ T :: *.

Proof: Routine induction, using Lemma 30.3.4(1) for the T-TAPP case.

Decidability

Space constraints preclude the inclusion in this book of a full proof of decidability for F_ω—i.e., a typechecking algorithm and proofs of its soundness, completeness, and termination—but almost all the required ideas are already familiar from the minimal typing algorithm for System F_<:in Chapter 28.

We begin by observing that the kinding relation is decidable (since its rules are syntax directed). This is no surprise, since we have seen that kinding is essentially a copy of the simply typed lambda-calculus "one level up." This assures us that the well-kindedness checks in the typing rules can be implemented effectively.

Next, we remove the one non-syntax-directed rule, T-EQ, from the typing relation, just as we removed T-SUB from F_<:. We then examine the other rules to see which premises must be generalized in order to account for essential uses of the now-missing T-EQ rule. It turns out there are two critical points.

In the first premise of rules T-APP and T-TAPP, we may need to use T-EQ to rewrite the type of the left-hand subexpression t₁ to bring an arrow or a quantifier to the outside. (For example, if the context associates variable x with type (λX.X→X)Nat, then the application x 5 has type Nat only because we can rewrite x's type as Nat→Nat.)

We accomplish this by introducing an analog of the exposure relation from §28.1. Here, rather than promoting t₁'s minimal type until it becomes an arrow or quantifier, as appropriate, we reduce it—for example, by repeatedly applying the rules in Figure 30-3 until no more nontrivial reductions are possible.^[2]

To be sure that this process will terminate, we need to show that our reduction rules are normalizing. Of course, on ill-kinded terms, reduction will not be normalizing, since the syntax of types in F_ω includes all the primitives we need to encode divergent terms such as omega (page 65). Fortunately, it follows from Proposition 30.3.19 that, as long as we start with a well-formed context (and perform appropriate kind-checks as we go along to ensure that any annotation we put into the context is well kinded), we need to deal only with well-kinded terms, and for these it is possible to show (by adapting the technique of Chapter 12, for example) that reduction always leads to a unique normal form.
In the second premise of T-APP, we may need to use equivalence to match the type T₂ calculated for t₂ with the left-hand side T₁₁ of the arrow type of t₁. An algorithmic variant of this rule will therefore include an equivalence check between T₂ and T₁₁. This check can be implemented, for example, by reducing both T₂ and T₁₁ to their respective normal forms and then testing whether these are identical (modulo the names of bound variables).

30.3.20 Exercise [⋆⋆⋆⋆]

Implement a typechecker for F_ω based on these ideas, using the purefsub checker as a starting point.

^[2]Actually, most typecheckers for F_ω use a less aggressive form of reduction known as weak head reduction, in which only leftmost, outermost redexes are reduced and we stop when some concrete constructor—i.e., anything other than an application—comes to the front of the type.

< Free Open Study >