26.4 Safety

< Free Open Study >

The type preservation property can be established quite directly for both the kernel and full variants of F_<:. We give proofs in detail here for kernel F_<:; the argument for full F_<: is very similar. When we consider subtyping and type-checking algorithms in Chapter 28, however, the two variants will turn out to be more different than the basic arguments in this chapter might suggest. We will find many points where the full system is much more complex to analyze than the kernel system, or indeed where the full system lacks useful properties (including decidable typechecking!) enjoyed by the kernel system.

We begin with some preliminary technical facts about the typing and sub-type relations. Their proofs proceed by routine induction on derivations.

26.4.1 Lemma [Permutation]

Suppose that Г is a well-formed context and that Δ is a permutation of Г—that is, Δ has the same bindings as Г, and their ordering in Δ preserves the scopes of type variables from Г, in the sense that, if one binding in Г introduces a type variable that is mentioned in another binding further to the right, then these bindings appear in the same order in Δ.

If Г ⊢ t : T, then Δ ⊢ t : T.
If Г ⊢ S <: T, then Δ ⊢ S <: T.

26.4.2 Lemma [Weakening]

If Г ⊢ t : T and Г, x:U is well formed, then Г x:U ⊢ t : T.
If Г ⊢ t : T and Г, X<:U is well formed, then Г, X<:U ⊢ t : T.
If Г ⊢ S <: T and Г, x:U is well formed, then Г, x:U ⊢ S <: T.
If Г ⊢ S <: T and Г, X<:U is well formed, then Г, X<:U ⊢ S <: T.

26.4.3 Exercise [⋆]

Where does the proof of weakening rely on permutation?

26.4.4 Lemma [Strengthening for Term Variables in Subtyping Derivations]

If Г, x:T, Δ ⊢ S <: T, then Г, Δ ⊢ S <: T.

Proof: Obvious: typing assumptions play no role in subtype derivations.

As usual, the proof of type preservation relies on several lemmas relating substitution with the typing and subtype relations.

26.4.5 Lemma [Narrowing]

If Г, X<:Q, Δ ⊢ S <: T and Г ⊢ P <: Q, then Г, X<:P, Δ ⊢ S <: T.
If Г, X<:Q, Δ ⊢ t : T and Г ⊢ P <: Q, then Г, X<:P, Δ ⊢ t : T.

These properties are often called narrowing because they involve restricting (narrowing) the range of the variable X.

Proof: Exercise [⋆].

Next, we have the usual lemma relating substitution and the typing relation.

26.4.6 Lemma [Substitution Preserves Typing]

If Г, x:Q, Δ ⊢ t : T and Г ⊢ q : Q, then Г, Δ ⊢ [x ↦ q]t : T.

Proof: Induction on a derivation of Г, x:Q, Δ ⊢ t : T, using the properties above.

Since we may substitute types for type variables during reduction, we also need a lemma relating type substitution and typing. The proof of this lemma (specifically, the T-SUB case) depends on a new lemma relating substitution and subtyping.

26.4.7 Definition

We write [X ↦ S]Г for the context obtained by substituting S for X in the right-hand sides of all of the bindings in Г.

26.4.8 Lemma [Type Substitution Preserves Subtyping]

If Г, X<:Q, Δ ⊢ S <: T and Г ⊢ P <: Q, then Г, [X ↦ P] Δ ⊢ [X ↦ P]S <: [X ↦ P]T.

Note that we need to substitute for X only in the part of the environment that follows the binding of X, since our conventions about scoping require that the types to the left of the binding of X do not contain X.

Proof: By induction on a derivation of Г, X<:Q, Δ ⊢ S <: T. The only interesting cases are the last two:

Case S-TVAR:

S = Y

Y<:T Î (Г, X<:Q, Δ)

There are two subcases to consider. If Y ≠ X, then the result is immediate from S-TVAR. On the other hand, if Y = X, then we have T = Q and [X ↦ P]S = Q, so the result follows by S-REFL.

Case S-ALL:	S = "Z<:U₁ .S₂	T = "Z<:U₁ .T₂
	Г, X<:Q, Δ, Z<:U₁ ⊢ S₂ <: T₂

By the induction hypothesis, Г, [X ↦ P]Δ, Z<:[X ↦ P]U₁ ⊢ [X ↦ P]S₂ <: [X ↦ P]T₂. By S-ALL, Г, [X ↦ P]Δ ⊢ "Z<:[X ↦ P]U₁ .[X ↦ P]S₂ <: "Z<:[X ↦ P]U₁ .[X ↦ P]T₂, that is, Г, [X ↦ P]Δ ⊢ [X ↦ P]("Z<:U₁ .S₂) <: [X ↦ P]("Z<:U₁ .T₂), as required.

A similar lemma relates type substitution and typing.

26.4.9 Lemma [Type Substitution Preserves Typing]

If Г, X<:Q, Δ ⊢ t : T and Г ⊢ P <: Q, then Г, [X ↦ P]Δ ⊢ [X ↦ P]t : [X ↦ P]T.

Proof: By induction on a derivation of Г, X<:Q, Δ ⊢ t : T. We give just the interesting cases.

Case T-TAPP:	t = t₁ [T₂]	Г, X<:Q, Δ ⊢ t₁ : "Z<:T₁₁ . T₁₂
	T = [Z ↦ T₂]T₁₂

By the induction hypothesis, Г, [X ↦ P]Δ ⊢ [X ↦ P]t₁ : [X ↦ P]("Z<:T₁₁ .T₁₂), i.e, Г, [X ↦ P]Δ ⊢ [X ↦ P]t₁ : "Z<:T₁₁ .[X ↦ P]T₁₂. By T-TAPP, Г, [X ↦ P]Δ ⊢[X ↦ P]t₁ [[X ↦ P]T₂] : [Z ↦ [X ↦ P]T₂]([X ↦ P]T₁₂), i.e., Г, [X ↦ P]Δ ⊢ [X ↦ P](t₁ [T₂]) : [X ↦ P]([Z ↦ T₂]T₁₂).

Case T-SUB:

Г, X<:Q, Δ ⊢ t : SГ, X<:Q, Δ ⊢ S <:T

By the induction hypothesis, Г, [X ↦ P] Δ ⊢ [X ↦ P]t : [X ↦ P]T. By the preservation of subtyping under substitution (Lemma 26.4.8), we have Г, [X ↦ P]Δ ⊢ [X ↦ P]S <: [X ↦ P]T, and the result follows by T-SUB.

Next, we establish some simple structural properties of subtyping.

26.4.10 Lemma [Inversion of the Subtype Relation, From Right to Left]

If Г ⊢ S <: X, then S is a type variable.
If Г ⊢ S <: T₁ → T₂, then either S is a type variable or else S has the form S₁ → S₂, with Г ⊢ T₁ <: S₁ and Г ⊢ S₂ <: T₂.
If Г ⊢ S <: "X<:U₁ . T₂, then either S is a type variable or else S has the form "X<:U₁ .S₂ with Г, X<:U₁ ⊢ S₂ <: T₂.

Proof: Part (1) is an easy induction on subtyping derivations. The only interesting case is the rule S-TRANS, which proceeds by two uses of the induction hypothesis, first on the right premise and then on the left premise. The arguments for the other parts are similar, using part (1) in the transitivity cases.

26.4.11 Exercise [Recommended, ⋆⋆]

Show the following "left to right inversion" properties:

If Г ⊢ S₁ →S₂ <: T, then either T = Top or else T = T₁ →T₂ with Г ⊢ T₁ <: S₁ and Г ⊢ S₂ <: T₂.
If Г ⊢ "X<:U.S₂ <: T, then either T = Top or else T = "X<:U.T₂ with Г, X<:U ↦; S₂ <: T₂.
If Г ⊢ X <: T, then either T = Top or T = X or Г ⊢ S <: T with X<:S Î Г.
If Г ⊢ Top <: T, then T = Top.

Lemma 26.4.10 is used, in turn, to establish one straightforward structural property of the typing relation that is needed in the critical cases of the type preservation proof.

26.4.12 Lemma

If Г ⊢ λx:S₁ .s₂ : T and Г ⊢ T <: U₁ → U₂, then Г ⊢ U₁ <: S₁ and there is some S₂ such that Г, x:S₁ ⊢ s₂ : S₂ and Г ⊢ S₂ <: U₂.
If Г ⊢ λX<:S₁ .s₂ : T and Г ⊢ T <: "X<:U₁ .U₂, then U₁ = S₁ and there is some S₂ such that Г, X<:S₁ ⊢ s₂ : S₂ and Г, X<:S₁ ⊢ S₂ <: U₂.

Proof: Straightforward induction on typing derivations, using Lemma 26.4.10 for the induction case (rule T-SUB).

With these facts in hand, the proof of type preservation is straightforward.

26.4.13 Theorem [Preservation]

If Г ⊢ t : T and t → t′, then Г ⊢ t′ : T.

Proof: By induction on a derivation of Г ⊢ t : T. All of the cases are straightforward, using the facts established above.

Case T-VAR, T-ABS, T-TABS:

t = x,

t = λx:T₁ .t₂,

t = λX<:U.t

These case cannot actually arise, since we assumed t → t′ and there are no evaluation rules for variables, abstractions, or type abstractions.

Case T-APP:

t = t₁ t₂

Г ⊢ t₁ : T₁₁→T₁₂

T = T₁₂

Г ⊢ t₂ : T₁₁

By the definition of the evaluation relation, there are three subcases:

Subcase:

Then the result follows from the induction hypothesis and T-APP.

Subcase:

t₁ is a value

Ditto.

Subcase:

t₁ = λx:U₁₁ .u₁₂

t′ = [x ↦ t₂]u₁₂

By Lemma 26.4.12, Г, x:U₁₁ ⊢ u₁₂ : U₁₂ for some U₁₂ with Г ⊢ T₁₁ <: U₁₁ and Г ⊢ U₁₂ <: T₁₂. By the preservation of typing under substitution (Lemma 26.4.6), Г ⊢ [x ↦ t₂]u₁₂ : U₁₂, from which we obtain Г ⊢ [x ↦ t₂]u₁₂ : T₁₂ by T-SUB.

Case T-TAPP:	t = t₁ [T₂]	Г ⊢ t : "X<:T₁₁ .T₁₂
	T = [X ↦ T₂]T₁₂	Г ⊢ T₂ <: T₁₁

By the definition of the evaluation relation, there are two subcases:

Subcase:

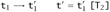
The result follows from the induction hypothesis and T-TAPP.

Subcase:

t₁ = λX<:U₁₁ .u₁₂

t′ = [X ↦ T₂]u₁₂

By Lemma 26.4.12, U₁₁ = T₁₁ and Г, X<:U₁₁ ⊢ u₁₂ : U₁₂ with Г, X<:U₁₁ ⊢ U₁₂ <: T₁₂. By the preservation of typing under substitution (Lemma 26.4.6), Г ⊢ [X ↦ T₂]u₁₂ : [X ↦ T₂]U₁₂, from which Г ⊢ [X ↦ T₂]u₁₂ : [X ↦ T₂]T₁₂ follows by Lemma 26.4.8 and T-SUB.

Case T-SUB:

Г ⊢ t : S

Г ⊢ S <:T

By the induction hypothesis, Г ⊢ t′ : S, and the result follows by T-SUB.

The progress theorem for F_<: is a straightforward extension of the one for the simply typed lambda-calculus with subtyping. As always, we begin by recording a canonical forms property telling us the possible shapes of closed values of arrow and quantifier types.

26.4.14 Lemma [Canonical Forms]

If v is a closed value of type T₁ → T₂, then v has the form λx:S₁ .t₂.
If v is a closed value of type "X<:T₁ .T₂, then v has the form λX<:T₁ .t₂.

Proof: Both parts proceed by induction on typing derivations; we give the argument just for the second part. By inspection of the typing rules, it is clear that the final rule in a derivation of ⊢ v : "X<:T₁ .T₂ must be either T-TABS or T-SUB. If it is T-TABS, then the desired result is immediate from the premise of the rule. So suppose the last rule is T-SUB. From the premises of this rule, we have ⊢ v : S and S <: "X<:T₁ .T₂. From the inversion lemma (26.4.10), we know that S has the form "X<:T₁ →S₂. The result now follows from the induction hypothesis.

With this in hand, the proof of progress is straightforward.

26.4.15 Theorem [Progress]

If t is a closed, well-typed F_<: term, then either t is a value or else there is some t′ with t → t′.

Proof: By induction on typing derivations. The variable case cannot occur because t is closed. The two cases for lambda-abstractions are immediate, since both term and type abstractions are values. The cases for application, type application, and subsumption are more interesting; we show just the latter two (term application is similar to type application).

Case T-TAPP:	t = t₁ [T₂]	⊢ t₁ : "X<:T₁₁ .T₁₂
	Г ⊢ T₂ <: T₁₁	T = [X ↦ T₂]T₂

By the induction hypothesis, either t₁ is a value or else it can make a step of evaluation. If t₁ can take a step, then rule E-TAPP1 applies to t. Otherwise, if t₁ is a value, then part (2) of the canonical forms lemma (26.4.14) tells us that t₁ has the form λX<:T₁₁ .t₁₂, so rule E-TAPPTABS applies to t.

Case T-SUB:

Г ⊢ t : S

Г ⊢ S <: T

The result follows directly from the induction hypothesis.

26.4.16 Exercise [⋆⋆⋆ ↛]

Extend the argument in this section to full F_<:.

< Free Open Study >