26.3 Examples

< Free Open Study >

This section presents some small examples of programming in F_<:. These examples are intended to illustrate the properties of the system, rather than to demonstrate its practical application; larger and more sophisticated examples will be found in later chapters (27 and 32). All the examples in this chapter work in both kernel and full F_<:.

Encoding Products

In §23.4, we gave an encoding of pairs of numbers in System F. This encoding can easily be generalized to pairs of arbitrary types: the elements of the type

   Pair T₁ T₂ = "X. (T₁→T₂→X) → X;

represent pairs of T₁ and T₂. The constructor pair and the destructors fst and snd are defined as follows. (The ascription in the definition of pair helps the typechecker print its type in a readable form.)

   pair = λX. λY. λx:X. λy:Y. (λR. λp:X→Y→R. p x y) as Pair X Y; ▸ pair : "X. "Y. X → Y → Pair X Y   fst = λX. λY. λp: Pair X Y. p [X] (λx:X. λy:Y. x); ▸ fst : "X. "Y. Pair X Y → X   snd = λX. λY. λpp: Pair X Y. p [Y] (λx:X. λy:Y. y); ▸ snd : "X. "Y. Pair X Y → Y

Clearly, the same encoding can be used in F_<:, since F_<: contains all the features of System F. What is more interesting, though, is that this encoding also has some natural subtyping properties. In fact, the expected subtyping rule for pairs

follows directly from the encoding.

26.3.1 Exercise [⋆ ↛]

Show this.

Encoding Records

It is interesting to observe that records and record types-including their subtyping laws-can actually be encoded in pure F_<:. The encoding presented here was discovered by Cardelli (1992).

We begin by defining flexible tuples as follows. They are "flexible" because they can be expanded on the right during subtyping, unlike ordinary tuples.

26.3.2 Definition

For each n ≥ 0 and types T₁ through T_n, let

In particular, . Similarly, for terms t₁ through t_n, let

where we elide the type arguments to pair, for the sake of brevity. (The term top here is just some arbitrary element of Top-i.e., an arbitrary closed, well-typed term.) The projection t.n (again eliding type arguments) is:

From this abbreviation, we immediately obtain the following rules for subtyping and typing of flexible tuples.

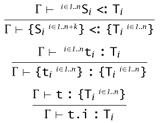
Now, let L be a countable set of labels, with a fixed total ordering given by the bijective function label-with-index : . We define records as follows.

26.3.3 Definition

Let L be a finite subset of L and let S_l be a type for each l Î L. Let m be the maximal index of any element of L, and

The record type {l:S_l^lÎL } is defined as the flexible tuple . Similarly, if t_l is a term for each l : L, then

The record value {l=t_l^lÎL} is . The projection t.l is just the tuple projection t.i, where label-with-index(i) = l.

This encoding validates the expected rules for typing and subtyping of records (rules S-RCDWIDTH, S-RCDDEPTH, S-RCDPERM, T-RCD, and T-PROJ from Figures 15-2 and 15-3). However, its interest is mainly theoretical-from a practical standpoint, the reliance on a global ordering of all field labels is a serious drawback: it means that, in a language with separate compilation, numbers cannot be assigned to labels on a module-by-module basis, but must instead be assigned all at once, i.e., at link time.

Church Encodings with Subtyping

As a final illustration of the expressiveness of F_<:, let's look at what happens when we add bounded quantification to the encoding of Church numerals in System F (§23.4). There, the type of Church numerals was:

   CNat = "X. (X→X) → X → X;

An intuitive anthropomorphic reading of this type is: "Tell me a result type T; now give me a function on T and a 'base element' of T, and I'll give you back another element of T formed by iterating the function you gave me n times over the base element you gave."

We can generalize this by adding two bounded quantifiers and refining the types of the parameters s and z.

   SNat = "X<:Top. "S<:X. "Z<:X. (X→S) → Z → X;

Intuitively, this type reads: "Give me a generic result type X and two subtypes S and Z. Now give me a function that maps from the whole set X into the subset S and an element of the special set Z, and I'll return you an element of X formed by iterating the function n times over the base element."

To see why this is interesting, consider this slightly different type:

   SZero = "X<:Top. "S<:X. "Z<:X. (X→S) → Z → Z;

Although SZero has almost the same form as SNat, it says something much stronger about the behavior of its elements, since it promises that its final result will be an element of Z, not just of X. In fact, there is just one way that this can happen-namely by yielding the argument z itself. In other words, the value

   szero = λX. λS<:X. λZ<:X. λs:X→S. λz:Z. z; ▸ szero : SZero

is the only inhabitant of the type SZero (in the sense that every other element of SZero behaves the same as szero). Since SZero is a subtype of SNat, we also have szero : SNat.

On the other hand, the similar type

   SPos = "X<:Top. "S<:X. "Z<:X. (X→S) → Z → S;

has more inhabitants; for example,

   sone   = λX. λS<:X. λZ<:X. λs:X→S. λz:Z. s z;   stwo   = λX. λS<:X. λZ<:X. λs:X→S. λz:Z. s (s z);   sthree = λX. λS<:X. λZ<:X. λs:X→S. λz:Z. s (s (s z));

and so on. Indeed, SPos is inhabited by all the elements of SNat except zsero.

We can similarly refine the typings of operations defined on Church numerals. For example, the type system can be used to check that the successor function always returns a positive number:

   ssucc = λn:SNat.             λX. λS<:X. λZ<:X. λs:X→S. λz:Z.               s (n [X] [S] [Z] s z); ▸ ssucc : SNat → SPos

Similarly, by refining the types of its parameters, we can write the function plus in such a way that the typechecker gives it the type SPos→SPos→SPos.

   spluspp = λn:SPos. λm:SPos.                λX. λS<:X. λZ<:X. λs:X→S. λz:Z.                  n [X] [S] [S] s (m [X] [S] [Z] s z); ▸ spluspp : SPos → SPos → SPos

26.3.4 Exercise [⋆⋆]

Write another variant of plus, identical to the one above except for type annotations, that has type SZero→SZero→SZero. Write one with type SPos→SNat→SPos.

The previous example and exercise raise an interesting point. Clearly, we don't want to write several different versions of plus with different names and then have to decide which to apply based on the expected types of its arguments: we want to have a single version of plus whose type contains all these possibilities-something like

   plus :   SZero→SZero→SZero          ∧ SNat→SPos→SPos          ∧ SPos→SNat→SPos          ∧ SNat→SNat→SNat

where t : S∧T means "t has both type S and type T." The desire to support this kind of overloading has led to the study of systems combining intersection types (§15.7) with bounded quantification. See Pierce (1997b).

26.3.5 Exercise [Recommended, ⋆⋆]

Following the model of SNat and friends, generalize the type CBool of Church booleans (§23.4) to a type SBool and two subtypes STrue and SFalse. Write a function notft with type SFalse→STrue and a similar one nottf with type STrue→SFalse.

26.3.6 Exercise [⋆ ↛]

We observed in the introduction to this chapter that subtyping and polymorphism can be combined in a more straightforward and orthogonal way than is done in F_<:. We start with System F (perhaps enriched with records, etc.) and add a subtype relation (as in the simply typed lambda-calculus with subtyping) but leave quantification unbounded. The only extension to the subtype relation is a covariant subtyping rule for the bodies of ordinary quantifiers:

Which examples in this chapter can be formulated in this simpler system?

< Free Open Study >