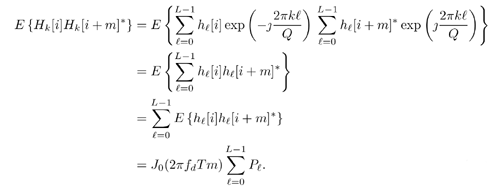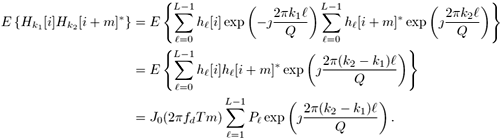10.2 OFDM Communication System

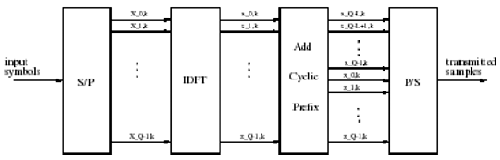
Figure 10.1 is a block diagram of an OFDM communication system. A serial-to-parallel buffer segments the information sequence into frames of Q symbols. An OFDM word at time i consists of Q data symbols X [ i ], X ₁ [ i ], ..., X _{Q -1} [ i ]. An inverse discrete Fourier transform (IDFT) is first applied to the OFDM word, to obtain

Figure 10.1. Block diagram of a simple OFDM transmitter.

Equation 10.1

A guard interval with cyclic prefix is then inserted to prevent possible intersymbol interference between OFDM words. After pulse shaping and parallel-to-serial conversion, the signals are then transmitted through a frequency-selective fading channel. The time-domain channel impulse response can be modeled as a tapped-delay line, given by

Equation 10.2

where denotes the maximum number of resolvable channel taps, with t _m being the maximum multipath spread and D _f being the carrier spacing. Assume that the channel taps remain constant over the interval of one OFDM word [i.e., a _l ( t ) a _l [( i -1) T ] for ( i -1) T t < iT , where T is the duration of one OFDM word]. At the receiver end, after matched filtering and removing the cyclic prefix, the sampled received signal corresponding to the n th OFDM word becomes

Equation 10.3

Equation 10.4

where * denotes the convolution, , and { n _m [ i ]} _m are i.i.d. complex white Gaussian noise samples. A DFT is then applied to the received signals { y _m [ i ]} _m to demultiplex the multicarrier signals:

Equation 10.5

For OFDM systems with proper cyclic extensions and proper sample timing, with tolerable leakage, the received signal after demultiplexing at the k th subcarrier can be expressed as

Equation 10.6

where { N _k [ i ]} _k contains the DFT of the noise samples { n _m [ i ]} _m , and ; and { H _k [ i ]} _k contains the DFT of channel impulse response { h _m [ i ]} _m :

Equation 10.7

Assume that for each l , 0 l < L , { h _l [ i ]} _i is a complex Gaussian process with an autocorrelation following the Jakes model:

Equation 10.8

where P _l is the average power of the l th tap and f _d is the Doppler spread. Assume further that the L fading processes are mutually independent. Since { H _k [ i ]} _k are linear transformations of { h _l [ i ]} _l , then for each k , 0 k < Q , { H _k [ i ]} _i is also a complex Gaussian process with autocorrelation

Equation 10.9

Hence from (10.6) and (10.9) it is seen that the received frequency-domain signal at each subcarrier k follows a flat-fading model with the same fading autocorrelation function as that in the time domain. Hence the OFDM system effectively transforms a frequency-selective fading channel into a set of parallel flat-fading channels. However, note that the frequency-domain channel responses of different carriers are correlated. In fact, we have

Equation 10.10