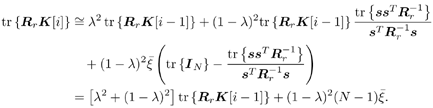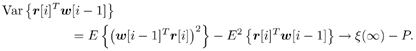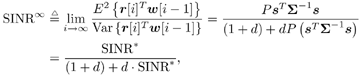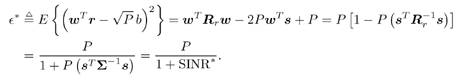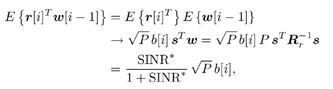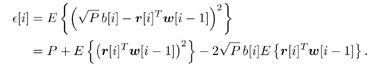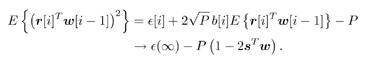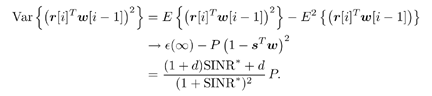7.9 Appendix: Convergence of the RLS Linear MMSE Detector
7.9.1 Linear MMSE Detector and RLS Blind Adaptation RuleConsider the following received signal model: Equation 7.151 where A K , b K and s K denote, respectively, the received amplitude, data bit, and the spreading waveform of the K th user ; i denotes the NBI signal; and Equation 7.152 where R r is the autocorrelation matrix of the received discrete signal r : Equation 7.153 The output SINR is given by Equation 7.154 where Equation 7.155 The mean output energy associated with w , defined as the mean-square output value of w applied to r , is Equation 7.156 where the last equality follows from (7.155) and the matrix inversion lemma. The mean-square error (MSE) at the output of w is Equation 7.157 The exponentially windowed RLS algorithm selects the weight vector w [ i ] to minimize the sum of exponentially weighted output energies: where 0 < l < 1 is a forgetting factor (1 - l << 1). The purpose of l is to ensure that the data in the distant past will be forgotten in order to provide tracking capability in nonstationary environments. The solution to this constrained optimization problem is given by Equation 7.158 where Equation 7.159 A recursive procedure for updating w [ i ] is as follows: Equation 7.160 Equation 7.161 Equation 7.162 Equation 7.163 In what follows we provide a convergence analysis for the algorithm above. In this analysis, we make use of three approximations/assumptions: (a) For large i , R r [ i ] is approximated by its expected value [111, 301]; (b) the input data r [ i ] and the previous weight vector w [ i “1] are assumed to be independent [175]; (c) some fourth-order statistic can be approximated in terms of a second-order statistic [175]. 7.9.2 Convergence of the Mean Weight VectorWe start by deriving an explicit recursive relationship between w [ i ] and w [ i “1]. Denote Equation 7.164 Premultiplying both sides of (7.161) by s T , we have Equation 7.165 From (7.165) we obtain Equation 7.166 where Equation 7.167 Substituting (7.161) and (7.166) into (7.162), we can write Equation 7.168 where Equation 7.169 is the a priori least-squares estimate at time i . It is shown below that Equation 7.170 Equation 7.171 Substituting (7.161) and (7.170) into (7.168), we have Equation 7.172 Premultiplying both sides of (7.172) by R r [ i ], we get Equation 7.173 where we have used (7.159) and (7.169). Let q [ i ] be the weight error vector between the weight vector w [ i ] at time n and the optimal weight vector w : Equation 7.174 Then from (7.173) we can deduce that Equation 7.175 Therefore, Equation 7.176 where Equation 7.177 in which we have used (7.171) and (7.169). It has been shown [111, 301] that for large i , the inverse autocorrelation estimate Equation 7.178 Using this approximation , we have Equation 7.179 Therefore, for large i , Equation 7.180 where we have used (7.170) and (7.179). For large i , R r [ i ] and R r [ i “1] can be assumed almost equal, and thus approximately [111, 301] Equation 7.181 Substituting (7.181) and (7.180) into (7.176), we then have Equation 7.182 Equation (7.182) is a recursive equation that the weight error vector q [ i ] satisfies for large i . In what follows we assume that the present input r [ i ] and the previous weight error q [ i “1] are independent. In this application of interference suppression, this assumption is satisfied when the interference signal consists of only MAI and white noise. If, in addition, there is NBI present, this assumption is not satisfied but is nevertheless assumed, as is the common practice in the analysis of adaptive algorithms [111, 175, 301]. Taking expectations on both sides of (7.182), we have where we have used the facts that s T w = s T w [ i ] = 1, s T q [ i ] = s T w [ i ] “ s T w = 0 and Equation 7.183 Therefore, the expected weight error vector always converges to zero, and this convergence is independent of the eigenvalue distribution. Finally, we verify (7.170) and (7.171). Postmultiplying both sides of (7.163) by r [ i ], we have Equation 7.184 On the other hand, (7.160) can be rewritten as Equation 7.185 Equation (7.170) is obtained by comparing (7.184) and (7.185). Multiplying both sides of (7.166) by s T k [ i ], we can write Equation 7.186 and (7.167) can be rewritten as Equation 7.187 Equation (7.171) is obtained comparing (7.186) and (7.187). 7.9.3 Weight Error Correlation MatrixWe proceed to derive a recursive relationship for the time evolution of the correlation matrix of the weight error vector q [ i ], which is the key to analysis of the convergence of the MSE. Let K [ i ] be the weight error correlation matrix at time n . Taking the expectation of the outer product of the weight error vector q [ i ], we get Equation 7.188 We next compute the four expectations appearing on the right-hand side of (7.188). First term Equation 7.189 Equation 7.190 Equation 7.191 Equation 7.192 Equation 7.193 where in (7.189) we have used (7.183); in (7.193) we have used (7.152); in (7.190) and (7.192) we have used the fact that Equation 7.194 Second term Equation 7.195 where we have used (7.183) and the following fact, which is shown below: Equation 7.196 Therefore, the second term is a transient term. Third term The third term is the transpose of the second term, and therefore it is also a transient term. Fourth term Equation 7.197 Equation 7.198 where in (7.198) we have used (7.152), and in (7.197) we have used the following fact, which is derived below: Equation 7.199 where Now combining these four terms in (7.188), we obtain (for large i ) Equation 7.200 Finally, we derive (7.194), (7.196), and (7.199). Derivation of (7.194) We use the notation [ ·] mn to denote the ( m, n )th entry of a matrix and [ ·] k to denote the k th entry of a vector. Then Equation 7.201 Next we use the Gaussian moment factoring theorem to approximate the fourth-order moment introduced in (7.201). The Gaussian moment factoring theorem states that if z 1 , z 2 , z 3 , and z 4 , are four samples of a zero-mean, real Gaussian process, then [175] Equation 7.202 Using this approximation, we proceed with (7.201): Equation 7.203 Therefore, where in the last equality we used (7.183) and the following fact: Equation 7.204 Derivation of (7.196) Similarly, we use the approximation by the Gaussian moment factoring formula and obtain since E { q [ i ]} Derivation of (7.199) Using the Gaussian moment factoring formula, we obtain 7.9.4 Convergence of MSE Next we consider the convergence of the output MSE. Let Equation 7.205 Equation 7.206 Since Equation 7.207 Since E { q [ i } Equation 7.208 Since l 2 + (1- l 2 ) < [ l + (1 - l )] 2 = 1, the term tr{ R r K [ i ]} converges. The steady-state excess mean-square error is then given by Equation 7.209 Again we see that the convergence of the MSE and the steady-state misadjustment are independent of the eigenvalue distribution of the data autocorrelation matrix, in contrast to the situation for the LMS version of the blind adaptive algorithm [183]. 7.9.5 Steady-State SINRWe now consider the steady-state output SINR of the RLS blind adaptive algorithm. At time i the mean output value is Equation 7.210 The variance of the output at time i is Equation 7.211 Let Equation 7.212 Therefore the steady-state SINR is given by Equation 7.213 where SINR * is the optimum SINR value given in (7.154). 7.9.6 Comparison with Training-Based RLS AlgorithmWe now compare the preceding results with the analogous results for the conventional RLS algorithms in which the data symbols b [ i ] are assumed to be known to the receiver. This condition can be achieved by using either a training sequence or decision feedback. In this case, the exponentially windowed RLS algorithm chooses w [ i ] to minimize the cost function Equation 7.214 The RLS adaptation rule in this case is given by [175] Equation 7.215 Equation 7.216 where e p [ i ] is the prediction error at time i and k [ i ] is the Kalman gain vector defined in (7.160). Using the results from [111], we conclude that the mean weight vector w [ i ] converges to w (i.e., E { w [ i ]} Equation 7.217 The MSE Equation 7.218 The steady-state excess mean-square error is given by [111] Equation 7.219 where we have used the approximation that Equation 7.220 where the last equality follows from (7.156). The output MSE at time i is Equation 7.221 Therefore, Equation 7.222 Using (7.220) and (7.222), after some manipulation, we have Equation 7.223 Therefore, the output SINR in the steady state is given by Equation 7.224 |
EAN: 2147483647
Pages: 91
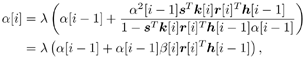
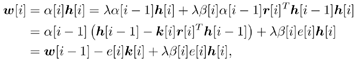
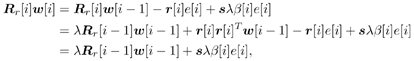
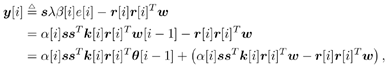
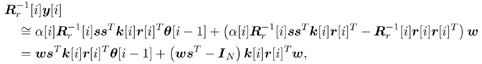
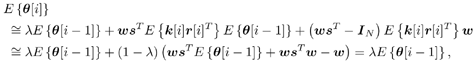
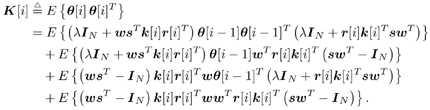
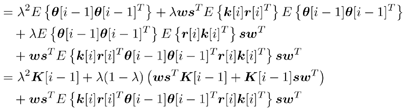
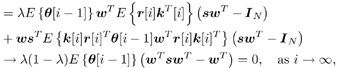
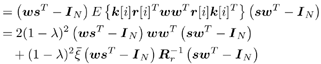
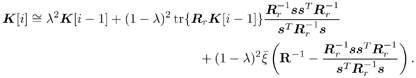
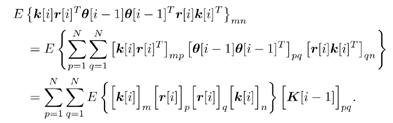
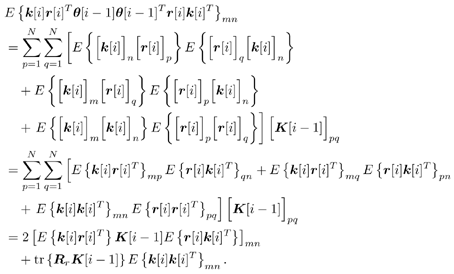
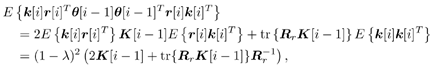
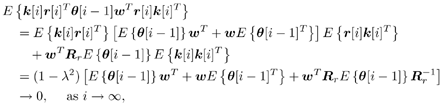
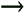 0.
0. 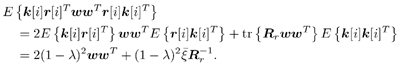
 [
[  , the last term in (7.207) is a transient term. Therefore, for large
, the last term in (7.207) is a transient term. Therefore, for large