5.3 Multivariate elastic random walk
5.3 Multivariate elastic random walk
From Assumption 1 the n underlying factors follow a multivariate joint elastic random walk [2] :
where ± i ( t, x )= a i + B ij x i . In matrix notation this linear system of equations becomes:
where
The short- term interest rate is expressed as a linear combination of the underlying stochastic factors (Assumption 2), hence:
where
-
x - vector of stochastic factors characterising the underlying economic system,
-
w - vector of weights which are either constants or functions of time.
The solution to (5.1) has the form [3] :
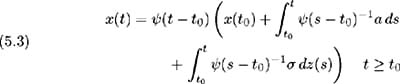
where ˆ ( t ˆ’ t ) is the matrix solution [ 33 ], [ 3 ]to:
In the special case where B is a constant:
and (5.3) becomes
For this special case [4] , the expected value and covariance matrix of x ( t ) and x ( t *)( t and t * are future points in time) are then calculated to be [5] :
where & pound ; is the covariance matrix:
with elements ƒ ij = ij ƒ i ƒ j where ij = ![]() [ dz i · dz j ].
[ dz i · dz j ].
[2] As usual dz i is the standard Wiener process with:
-
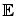 [ dz i ] = 0,
[ dz i ] = 0, -
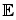 [ dz i dz i ] = dt .
[ dz i dz i ] = dt .
[3] The deterministic system of equations corresponding to (5.1) is:
This is a linear system, which has a solution of the form
where ½ ( t ) is some function of time and ˆ ( t ˆ’ t ) is the solution to the homogeneous matrix equation
with initial condition ˆ ( t ˆ’ t )= I , and hence it is the fundamental matrix of the system (5.4).
Matrix equation (5.4) now becomes:
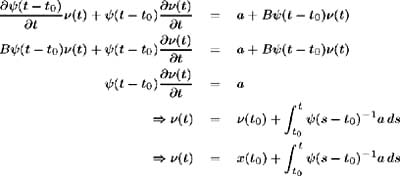
and hence the solution to the deterministic system is:
Now consider the system of stochastic equations
which has solution
Applying Ito's Lemma to x ( t )= ˆ ( t ˆ’ t ) ½ ( t )
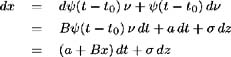
which is the original differential system (5.1). Hence, we have shown that the solution to this system is
[4] The calculations are shown for the special case due to the simplified notation, however the more general case proceeds in a similar fashion.
[5] The covariance is calculated as follows :
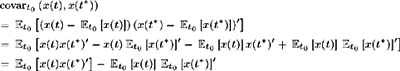
Consider:

and so:
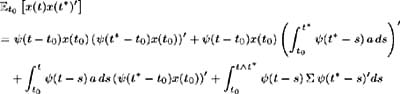
Also:

and hence (5.7) follows.
EAN: 2147483647
Pages: 132