4.2 Equilibrium term structure
4.2 Equilibrium term structure
Let P ( r, V, ) be the price of a risk-free discount bond with time to maturity. The value of this discount bond must satisfy the fundamental partial differential equation for the value of a contingent claim (4.6),within the equilibrium economy outlined earlier.
4.2.1 Discount bond price
The equilibrium value of P ( x, y, )may be found by solving (4.6) subject to the terminal boundary condition P ( x, y, 0) = 1. This equilibrium value has the form:
where
and
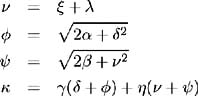
Applying the change of variables from x and y to r and V , the discount bond price may be represented as [6] :
where
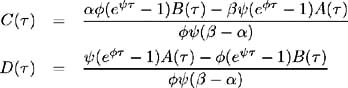
The utility-dependent market price of risk parameter » , enters the bond price equation via the parameter ½ . This means it need not be estimated separately, but only in a functional form with parameter ¾ . The exponential form of the bond price solution (4.28) ensures the tractability of the closed- form solution and simplifies its calculation.
4.2.2 Yield to maturity
Let Y ( ) be the yield to maturity on a discount bond with term to maturity. Hence:
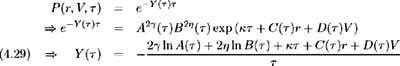
which indicates that the yield on any discount bond with maturity , is a linear function of state variables r and V . We can show [7] that lim ’ Y ( ) = r , which is consistent with our definition of r as the instantaneous short-term interest rate.
We may also show [8] that lim ’ˆ Y ( ) = ³ ( ˆ’ ) + · ( ˆ ˆ’ ½ ) which is a constant, independent of current values of r and V . This is consistent with the above analysis that r and V have long-run stationary distributions and hence the influence of the current level of the interest rate diminishes for yields far into the future.
4.2.3 Shape of the yield curve
One of the shortcomings of one factor yield curve models is the restrictions they place on possible shapes the term structure can assume. The advantage of the current model is that the dependence of discount bond prices on both the short-term interest rate and volatility of the short-term interest rate introduces greater freedom to the shape of the term structure. The sign of [9] P r ( r, V, ) is indeterminate and so changes in the short-term interest rate may introduce varying, often opposite , changes on the yield curve at different maturities. Short-term interest rate volatility V may change while r remains constant. Changes in V may affect the slope and volatility of the yield curve, often to different degrees at various maturities, changing the overall shape of the term structure. In fact, very complex yield curve shapes can be obtained with relatively easy manipulations of the parameters of the underlying state variables r and V .
4.2.4 Term structure of volatility
For the purposes of option pricing, it is important to correctly fit the yield curve and the term structure of volatilities [ 45 ]. Determining the volatility at various points on the yield curve is equivalent to determining bond yield volatilities for various maturities . To calculate the yield volatility, first use Ito's Lemma to calculate bond price volatility and then use Ito's Lemma again to find the yield volatility.
Volatilities of discount bond prices for various maturities may be derived by applying Ito's Lemma to (4.28):

and since z 2 and z 3 are uncorrelated the variance of bond price returns becomes:
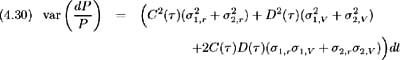
From (4.28) we have:
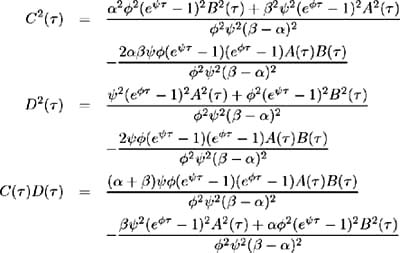
Also:
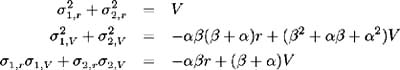
Hence the variance, (4.30) may be expressed as:

Grouping and simplifying the coefficients of r and V , the variance of bond price returns becomes:
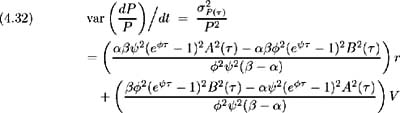
Finally, to derive the volatility of bond yields, apply Ito's Lemma to the expression Y ( ) = ˆ’ ln P ( )/ as in [ 45 ]:
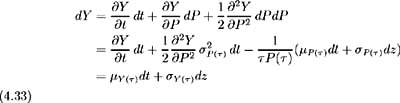
and so:
The volatility of bond price returns and hence bond yield volatility is a function of the term to maturity , as well as the underlying variables r and V . This implies a term structure of volatilities that may assume a wider variety of shapes than is possible for one factor models.
4.2.5 Correlation between rates of various maturities
One of the advantages of a two factor model over a one factor model, is that it allows for imperfect correlation between rates of various maturities. To determine this correlation, we calculate the correlation between yields on discount bonds of various maturities.
From (4.29), we may write the yield to maturity of a maturity bond as [10] :
Applying Ito's Lemma to (4.35) and making use of (4.12) and (4.13):

and so:
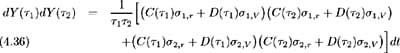
By the definition of correlation we have:
Since Y ( 1 ) and Y ( 2 ) are Wiener processes, ![]() [ dY ( 1 )] =
[ dY ( 1 )] = ![]() [ dY ( 1 )] = 0 and hence:
[ dY ( 1 )] = 0 and hence:
and (4.37) becomes:
Finally, using (4.36) the correlation may be expressed as:
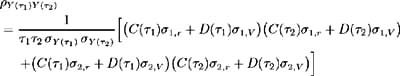
where the variances, ƒ 2 Y ( 1 ) and ƒ 2 Y ( 2 ) may be obtained by taking expectations of (4.35) or by making use of bond price volatilities and (4.34).
[6] First, substituting (4.10) and (4.11) into the exponent in (4.25) we have:
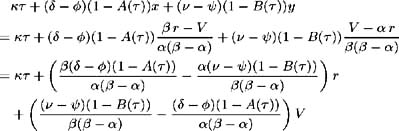
From (4.26) and (4.27) we have:

as well as
and so we may continue as
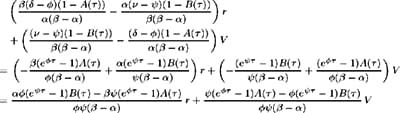
[7] It is easy to see that both the numerator and denominator of Y ( ) tend to zero as tends to zero. Hence apply L'Hopital's Rule. We have:
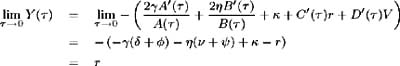
since, by definition = ³ ( + )+ · ( ½ + ˆ ).
[8] Again, apply L'Hopital's Rule to Y ( ):
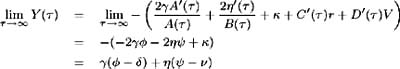
by the definition of .
[9] Subscript indicates a partial derivative.
[10] Here ![]()
EAN: 2147483647
Pages: 132