2.2 Equilibrium risk-free rate of interest
2.2 Equilibrium risk-free rate of interest
We need to determine the equilibrium values of a , r and ² . The solution to an individual's planning problem consists of an optimal physical investment policy a *, optimal consumption plan C * and the associated indirect utility function J *. By writing the portfolio allocation (physical investment) part as a quadratic programming problem, CIR [ 17 ] determine the equilibrium interest rate to be of the form:
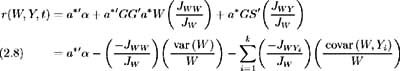
Interest Rate Modelling (Finance and Capital Markets Series)
ISBN: 1403934703
EAN: 2147483647
EAN: 2147483647
Year: 2004
Pages: 132
Pages: 132
Authors: Simona Svoboda