Cryptography: Theory and Practice:The RSA System and Factoring
 | Cryptography: Theory and Practice by Douglas Stinson CRC Press, CRC Press LLC ISBN: 0849385210 Pub Date: 03/17/95 |
| Previous | Table of Contents | Next |
Example 4.10
Suppose n = 403 = 13 × 31. The four square roots of 1 modulo 403 are 1, 92, 311 and 402. The square root 92 is obtained by solving the system x ≡ 1 (mod 13), x ≡ -1 (mod 31) using the Chinese remainder theorem. Having found this non-trivial square root, the other non-trivial square root must be 403 - 92 = 311. It is the solution to the system x ≡ -1 (mod 13), x ≡ 1 (mod 31).
Suppose x is a non-trivial square root of 1 modulo n. Then we have
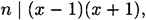
but n divides neither factor on the right side. It follows that gcd(x + 1, n) = p or q (and similarly, gcd(x - 1, n) = p or q). Of course, a greatest common divisor can be computed using the Euclidean algorithm, without knowing the factorization of n. Hence, knowledge of a non-trivial square root of 1 modulo n yields the factorization of n with only a polynomial amount of computation. This important fact is the basis of many results in cryptography.
In Example 4.10 above, gcd(93,403) = 31 and gcd(312,403) = 13.
In Figure 4.10, we present an algorithm which, using the hypothetical algorithm A as a subroutine, attempts to factor n by finding a non-trivial square root of 1 modulo n. (Recall that A computes the decryption exponent a corresponding to the encryption exponent b.) We first do an example to illustrate the application of this algorithm.
Example 4.11
Suppose n = 89855713, b = 34986517 and a = 82330933, and the random value w = 5. We have
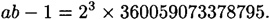
In step 6, v = 85877701, and in step 10, v = 1. In step 12, we compute

This is one factor of n; the other is n/9103 = 9871.
Let’s now proceed to the analysis of the algorithm. First, observe that if we are lucky enough to choose w to be a multiple of p or q, then we can factor n

Figure 4.10 Factoring algorithm, given the decryption exponent a
immediately. This is detected in step 2. If w is relatively prime to n, then we compute wr, w2r, w4r, . . . , by successive squaring, until
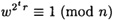
for some t. Since
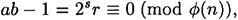
we know that 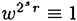 (mod n). Hence, the while loop terminates after at most s iterations. At the end of the while loop, we have found a value v0 such that
(mod n). Hence, the while loop terminates after at most s iterations. At the end of the while loop, we have found a value v0 such that 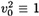 (mod n) but
(mod n) but 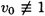 (mod n). If v0 ≡ -1 (mod n), then the algorithm fails; otherwise, v0 is a non-trivial square root of 1 modulo n and we are able to factor n (step 12).
(mod n). If v0 ≡ -1 (mod n), then the algorithm fails; otherwise, v0 is a non-trivial square root of 1 modulo n and we are able to factor n (step 12).
The main task facing us now is to prove that the algorithm succeeds with probability at least 1/2. There are two ways in which the algorithm can fail to factor n:
- 1. wr ≡ 1 (mod n) (step 7)
- 2.
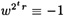 (mod n) for some t, 0 ≤ t ≤ s - 1 (step 11)
(mod n) for some t, 0 ≤ t ≤ s - 1 (step 11) - 2.
We have s + 1 congruences to consider. If a random value w is a solution to at least one of these s + 1 congruences, then it is a “bad” choice, and the algorithm fails. So we proceed by counting the number of solutions to each of these congruences.
First, consider the congruence wr ≡ 1 (mod n). The way to analyze a congruence such as this is to consider solutions modulo p and modulo q separately, and then combine them using the Chinese remainder theorem. Observe that x ≡ 1 (mod n) if and only if x ≡ 1 (mod p) and x ≡ 1 (mod q).
So, we first consider wr ≡ 1 (mod p). Since p is prime, 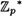 is a cyclic group by Theorem 4.7. Let g be a primitive element modulo p. We can write w = gu for a unique integer u, 0 ≤ u ≤ p - 2. Then we have
is a cyclic group by Theorem 4.7. Let g be a primitive element modulo p. We can write w = gu for a unique integer u, 0 ≤ u ≤ p - 2. Then we have
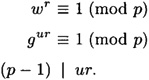
| Previous | Table of Contents | Next |
Copyright © CRC Press LLC
EAN: 2147483647
Pages: 133