Cryptography: Theory and Practice:The RSA System and Factoring | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

THEOREM 4.10

The Miller-Rabin algorithm for Composites is a yes-biased Monte Carlo algorithm.

PROOF We will prove this by assuming the algorithm answers “n is composite” for some prime integer n, and obtain a contradiction. Since the algorithm answers “n is composite,” it must be the case that 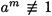(mod n). Now consider the sequence of values b tested in the algorithm. Since b is squared in each iteration of the for loop, we are testing the values . Since the algorithm answers “n is composite,” we conclude that

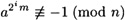
for 0 ≤ i ≤ k - 1.

Figure 4.9 The Miller-Rabin primality test for an odd integer n

Now, using the assumption that n is prime, Fermat’s theorem (Corollary 4.6) tells us that

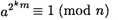
since n - 1 = 2^km. Then 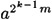is a square root of 1 modulo n. Since n is prime, there are only two square roots of 1 modulo n, namely, ±1 mod n. This can be seen as follows: x is a square root of 1 modulo n if and only if

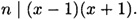
Since n is prime, either n | (x - 1) (i.e., x ≡ 1 (mod n)) or n | (x + 1) (i.e., x ± 1 (mod n)).

We have that

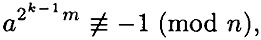
so it follows that

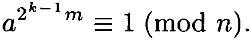
Then 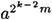must be a square root of 1. By the same argument,

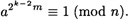
Repeating this argument, we eventually obtain

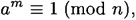
which is a contradiction, since the algorithm would have answered “n is prime” in this case.

It remains to consider the error probability of the Miller-Rabin algorithm. Although we will not prove it here, the error probability can be shown to be, at most, 1/4.

4.6 Attacks On RSA

In this section, we address the question: are there possible attacks on RSA other than factoring n? Let us first observe that it is sufficient for the cryptanalyst to compute φ(n). For, if n and φ(n) are known, and n is the product of two primes p, q, then n can be easily factored, by solving the two equations

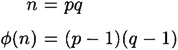
for the two “unknowns” p and q. If we substitute q = n/p into the second equation, we obtain a quadratic equation in the unknown value p:

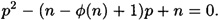
The two roots of this equation will be p and q, the factors of n. Hence, if a cryptanalyst can learn the value of φ(n), then he can factor n and break the system. In other words, computing φ(n) is no easier than factoring n.

Here is an example to illustrate.

Example 4.9

Suppose the cryptanalyst has learned that n = 84773093 and φ(n) = 84754668. This information gives rise to the following quadratic equation:

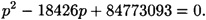
This can be solved by the quadratic formula, yielding the two roots 9539 and 8887. These are the two factors of n.

4.6.1 The Decryption Exponent

We will now prove the very interesting result that any algorithm which computes the decryption exponent a can be used as a subroutine (or oracle) in a probabilistic algorithm that factors n. So we can say that computing a is no easier than factoring n. However, this does not rule out the possibility of breaking the cryptosystem without computing a.

Notice that this result is of much more than theoretical interest. It tells us that if a is revealed, then the value n is also compromised. If this happens, it is not sufficient for Bob to choose a new encryption exponent; he must also choose a new modulus n.

The algorithm we are going to describe is a probabilistic algorithm of the Las Vegas type. Here is the definition:

DEFINITION 4.5 Suppose 0 ≤ ∈ < 1 is a real number. A Las Vegas algorithm is a probabilistic algorithm such that, for any problem instance I, the algorithm may fail to give an answer with some probability ∈ (i.e., it can terminate with the message “no answer”). However, if the algorithm does return an answer, then the answer must be correct.

REMARK Las Vegas algorithm may not give an answer, but any answer it gives is correct. In contrast, a Monte Carlo algorithm always gives an answer, but the answer may be incorrect.

If we have a Las Vegas algorithm to solve a problem, then we simply run the algorithm over and over again until it finds an answer. The probability that the algorithm will return “no answer” m times in succession is ∈^m. The average (i.e., expected) number of times the algorithm must be run in order to obtain an answer is in fact 1/(1 - ∈) (see the exercises).

Suppose that A is a hypothetical algorithm that computes the decryption exponent a from b and n. We will describe a Las Vegas algorithm that uses A as an oracle. This algorithm will factor n with probability at least 1/2. Hence, if the algorithm is run m times, then n will be factored with probability at least 1 - 1/2^m.

The algorithm is based on certain facts concerning square roots of 1 modulo n, where n = pq is the product of two distinct odd primes. Recall that the congruence x² ≡ 1 (mod p) has two solutions modulo p, namely x = ±1 mod p. Similarly, the congruence x² ≡ 1 (mod q) has two solutions, namely x = ±1 mod q.

Now, since x² ≡ 1 (mod n) if and only if x² ≡ 1 (mod p) and x² ≡ 1 (mod q), it follows that x² ≪ 1 (mod n) if and only if x² ≡ 1 mod p and x = ±1 mod q. Hence, there are four square roots of 1 modulo n, and they can be found using the Chinese remainder theorem. Two of these solutions are x = ±1 mod n; these are called the trivial square roots of 1 modulo p. The other two square roots are called non-trivial, and they are negatives of each other modulo n.

Here is a small example to illustrate.

Table of Contents