Cryptography: Theory and Practice:Shannon s Theory | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

2.6 Notes

The idea of perfect secrecy and the use of entropy techniques in cryptography was pioneered by Shannon [SH49]. Product cryptosystems are also discussed in this paper. The concept of entropy was defined by Shannon in [SH48]. Good introductions to entropy, Huffman coding and related topics can be found in the books by Welsh [WE88] and Goldie and Pinch [GP91].

The results of Section 2.4 are due to Beauchemin and Brassard [BB88], who generalized earlier results of Shannon.

Exercises

2.1 Let n be a positive integer. A Latin square of order n is an n × n array L of the integers 1, ..., n such that every one of the n integers occurs exactly once in each row and each column of L. An example of a Latin square of order 3 is as follows:

1	2	3
3	1	2
2	3	1

Given any Latin square L of order n, we can define a related cryptosystem. Take . For 1 ≤ i ≤ n, the encryption rule e_i is defined to be e_i(j) = L(i, j). (Hence each row of L gives rise to one encryption rule.)

Give a complete proof that this Latin square cryptosystem achieves perfect secrecy.

2.2 Prove that the Affine Cipher achieves perfect secrecy.

2.3 Suppose a cryptosystem achieves perfect secrecy for a particular plaintext probability distribution p₀. Prove that perfect secrecy is maintained for any plaintext probability distribution.

2.4 Prove that if a cryptosystem has perfect secrecy and

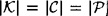, then every ciphertext is equally probable.

2.5 Suppose X is a set of cardinality n, where 2^k ≤ n < 2^k+1, and p(x) = 1/n for all x ∈ X.

(a) Find a prefix-free encoding of X, say f, such that

HINT Encode 2^k+1 - n elements of X as strings of length k, and encode the remaining elements as strings of length k + 1.

(b) Illustrate your construction for n = 6. Compute

and H(X) in this case.

2.6 Suppose X = {a, b, c, d, e} has the following probability distribution: p(a) = .32, p(b) = .23, p(q) = .20, p(d) = .15 and p(e) = .10. Use Huffman’s algorithm to find the optimal prefix-free encoding of X. Compare the length of this encoding to H(X).

2.7 Prove that H(X, Y) = H(Y) + H(X|Y). Then show as a corollary that H(X|Y) ≤ H(X), with equality if and only if X and Y are independent.

2.8 Prove that a cryptosystem has perfect secrecy if and only if H(P|C) = H(P).

2.9 Prove that, in any cryptosystem, H(K|C) ≥ H(P|C). (Intuitively, this result says that, given a ciphertext, the opponent’s uncertainty about the key is at least as great as his uncertainty about the plaintext.)

2.10 Consider a cryptosystem in which

. Suppose the encryption matrix is as follows:

Given that keys are chosen equiprobably, and the plaintext probability distribution is , compute H(P), H(C), H(K), H(K|C) and H(P|C).

2.11 Compute H(K|C) and H(K|P, C) for the Affine Cipher.

2.12 Consider a Vigenere Cipher with keyword length m. Show that the unicity distance is 1/R_L, where R_L is the redundancy of the underlying language. (This result is interpreted as follows. If n₀ denotes the number of alphabetic characters being encrypted, then the “length” of the plaintext is n₀/m, since each plaintext element consists of m alphabetic characters. So, a unicity distance of 1/R_L corresponds to a plaintext consisting of m/R_L alphabetic characters.)

2.13 Show that the unicity distance of the Hill Cipher (with an m × m encryption matrix) is less than m/R_L (Note that the number of alphabetic characters in a plaintext of this length is m²/R_L.)

2.14 A Substitution Cipher over a plaintext space of size n has

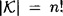Stirling’s formula gives the following estimate for n!: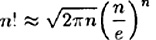

(a) Using Stirling’s formula, derive an estimate of the unicity distance of the Substitution Cipher.

(b) Let m ≥ 1 be an integer. The m-gram Substitution Cipher is the Substitution Cipher where the plaintext (and ciphertext) spaces consist of all 26^m m-grams. Estimate the unicity distance of the m-gram Substitution Cipher if R_L = 0.75.

2.15 Prove that the Shift Cipher is idempotent.

2.16 Suppose S₁ is the Shift Cipher (with equiprobable keys, as usual) and S₂ is the Shift Cipher where keys are chosen with respect to some probability distribution

(which need not be equiprobable). Prove that S₁ × S₂ = S₁.

2.17 Suppose S₁ and S₂ are Vigenere Ciphers with keyword lengths m₁, m₂ respectively, where m₁ > m₂.

(a) If m₂ | m₁, then show that S₂ × S₁ = S₁.

(b) One might try to generalize the previous result by conjecturing that S₂ × S₁ = S₃, where S₃ is the Vigenere Cipher with keyword length lcm(m₁, m₂). Prove that this conjecture is false.

HINT If 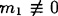mod m₂, then the number of keys in the product cryptosystem S₂ × S₁ is than the number of keys in S₃.

Table of Contents