Cryptography: Theory and Practice:Secret Sharing Schemes
 | Cryptography: Theory and Practice by Douglas Stinson CRC Press, CRC Press LLC ISBN: 0849385210 Pub Date: 03/17/95 |
| Previous | Table of Contents | Next |
THEOREM 11.11
Suppose G is a connected graph that is not a complete multipartite graph. Let Γ(G) be the access structure that is the closure of E, where E is the edge set of G. Then ρ*(Γ(G)) ≤ 2/3.
PROOF We will first prove that any connected graph that is not a complete multipartite graph must contain four vertices w, x, y, z such that the induced subgraph G[w, x, y, z] is isomorphic to either the basis of access structure # 5 or # 8.
Let GC denote the complement of G. Since G is not a complete multipartite graph, there must exist three vertices x, y, z such that xy, yz ∈ E(GC) and xz ∈ E(G). Define
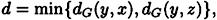
where dG denotes the length of a shortest path (in G) between two vertices. Then d ≥ 2. Without loss of generality, we can assume that d = dG (y, x) by symmetry.
Let

be a path in G, where yo = y. We have that
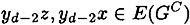
and
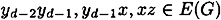
It follows that G[yd-2, yd-1, x, z] is isomorphic to the basis of access structure # 5 or # 8, as desired.
So, we can assume that we have found four vertices w, x, y, z such that the induced subgraph G[w, x, y, z] is isomorphic to either the basis of access structure #5 or # 8. Now, let 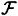 be any scheme realizing the access structure Γ(G). If we restrict the domain of the distribution rules to {w, x, y, z}, then we obtain a scheme
be any scheme realizing the access structure Γ(G). If we restrict the domain of the distribution rules to {w, x, y, z}, then we obtain a scheme  realizing access structure # 5 or # 8. It is also obvious that
realizing access structure # 5 or # 8. It is also obvious that 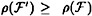 . Since
. Since 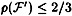 , it follows that
, it follows that 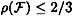 . This completes the proof.
. This completes the proof.
Since ρ* = 1 for complete multipartite graphs, Theorem 11.11 tells us that it is never the case that 2/3 < ρ* < 1 for any access structure that is the closure of the edge set of a connected graph.
11.8 The Decomposition Construction
We still have four access structures in Table 11.1 to consider. Of course, we can use the monotone circuit construction to produce schemes for these access structures. However, by this method, the best we can do is to obtain information rate ρ = 1/2 in each case. We can get ρ = 1/2 in cases # 5 and # 12 by using a disjunctive normal form boolean circuit. For cases # 8 and # 13, a disjunctive normal form boolean circuit will yield ρ = 1/3, but other monotone circuits exist which allow us to attain ρ = 1/2. But in fact, it is possible to construct schemes with ρ = 2/3 for each of these four access structures, by employing constructions that use ideal schemes as building blocks in the construction of larger schemes.
We present a construction of this type called the “decomposition construction.” First, we need to define an important concept.
DEFINITION 11.6 Suppose Γ is an access structure having basis Γ0. Let 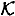 be a specified key set. An ideal
be a specified key set. An ideal 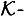 decomposition of Γ0 consists of a set {Γ1, . . . Γn} such that the following properties are satisfied:
decomposition of Γ0 consists of a set {Γ1, . . . Γn} such that the following properties are satisfied:
- 1.
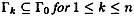
- 2.
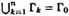
- 3. for 1 ≤ k ≤ n, there exists an ideal scheme with key set
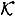 , on the subset of participants
, on the subset of participants 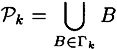
for the access structure having basis Γk.
- 2.
Given an ideal 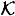 -decomposition of an access structure Γ, we can easily construct a perfect secret sharing scheme, as described in the following theorem.
-decomposition of an access structure Γ, we can easily construct a perfect secret sharing scheme, as described in the following theorem.
THEOREM 11.12
Suppose Γ is an access structure having basis Γ0. Let 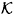 be a specified key set, and suppose {Γ1,...Γn} is an ideal
be a specified key set, and suppose {Γ1,...Γn} is an ideal 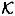 -decomposition of Γ. For every participant Pi, define
-decomposition of Γ. For every participant Pi, define
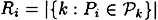
Then there exists a perfect secret sharing scheme realizing Γ, having information rate ρ 1/R, where
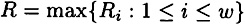
PROOF For 1 ≤ k ≤ n, we have an ideal scheme realizing the access structure with basis Γk, with key set 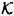 , having
, having 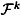 as its set of distribution rules. We will construct a scheme realizing Γ, with key set
as its set of distribution rules. We will construct a scheme realizing Γ, with key set 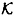 . The set of distribution rules
. The set of distribution rules 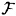 is constructed according to the following recipe. Suppose D wants to share a key K. Then, for 1 ≤ k ≤ n, he chooses a random distribution rule
is constructed according to the following recipe. Suppose D wants to share a key K. Then, for 1 ≤ k ≤ n, he chooses a random distribution rule 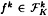 and distributes the resulting shares to the participants in
and distributes the resulting shares to the participants in 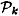 .
.
We omit the proof that the scheme is perfect. However, it is easy to compute the information rate of the resulting scheme. Since each of the component schemes is ideal, it follows that
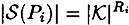
for 1 ≤ i ≤ w. So
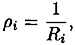
and
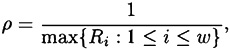
which is what we were required to prove.
Although Theorem 11.12 is useful, it is often much more useful to employ a generalization in which we have 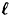 ideal
ideal 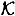 -decompositions of Γ0 instead of just one. Each of the
-decompositions of Γ0 instead of just one. Each of the 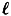 decompositions is used to share a key chosen from
decompositions is used to share a key chosen from 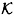 . Thus, we build a scheme with key set
. Thus, we build a scheme with key set 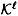 . The construction of the scheme and its information rate are as stated in the following theorem.
. The construction of the scheme and its information rate are as stated in the following theorem.
| Previous | Table of Contents | Next |
Copyright © CRC Press LLC
EAN: 2147483647
Pages: 133