Cryptography: Theory and Practice:Secret Sharing Schemes | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

THEOREM 11.13 (Decomposition Construction)

Suppose Γ is an access structure having basis Γ₀, and 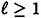is an integer. Let be a specified key set, and for 1 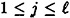, suppose that 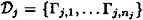is an ideal decomposition of Γ₀. Let 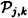denote the participant set for the access structure Γ_j,k. For every participant P_i, define

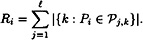
Then there exists a perfect secret sharing scheme realizaing Γ, having information rat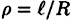e where

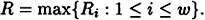
PROOF For 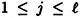and 1 ≤ k ≤ n, we have an ideal scheme realizing the access structure with basis Γ_j,k, with key set 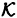, having as its set of distribution rules. We construct a scheme realizing Γ, with key set 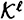. The set of distribution rules 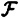is constructed according to the following recipe. Suppose D wants to share a key 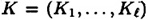. Then for 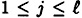and 1 ≤ k ≤ n, he chooses a random distribution rule 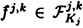and distributes the resulting shares to the participants in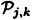

The information rate can be computed in a manner similar to that of Theorem 11.12.

Let's look at a couple of examples.

Example 11.10

Consider access structure # 5. The basis is a graph that is not a complete multi-partite graph. Therefore we know from Theorem 11.11 that ρ* ≤ 2/3.

Let p be prime, and consider the following two ideal 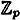-decompositions:

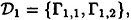
where

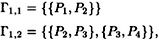
and

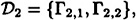
where

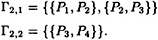
Each decomposition consists of a K₂ and a K_1,2, so they are indeed ideal 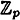-decompositions. Either of them yields a scheme with ρ = 1/2. However, if we “combine” them by applying Theorem 11.13 with 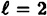, then we get a scheme with ρ = 2/3, which is optimal.

One implementation of the scheme, using Theorem 11.5, is as follows. D will choose four random elements (independently) from 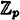, say b₁₁, b₁₂, b₂₁, and b₂₂. Given a key 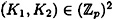, D distributes shares as follows:

1. P₁ receives b₁₁, b₂₁.

2. P₂ receives b₁₁ + K₁, b₁₂, b₂₁ + K₂.

3. P₃ receives b₁₂ + K₁, b₂₁, b₂₂.

4. P₄ receives b₁₂, b₂₂ + K₂.

(All arithmetic is performed in .)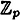

Example 11.11

Consider access structure # 8. Again, ρ* ≤ 2/3 by Theorem 11.11, and two suitable ideal compositions will yield an (optimal) scheme with ρ = 2/3.

Take 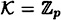for any prime p ≥ 3, and define two ideal 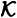-decompositions to be:

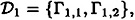
where

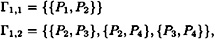
and

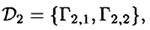
where

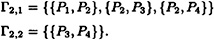
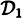consists of a K₂ and a K₃, and 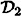consists of a K₂ and a K_1,3, so both are ideal -decompositions. Applying Theorem 11.13 with , we get a scheme with ρ = 2/3.

One implementation, using Theorem 11.5, is as follows. D will choose four random elements (independently) from 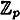, say b₁₁, b₁₂, b₂₁, and b₂₂. Given a key 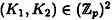, D distributes shares as follows:

1. P₁ receives b₁₁ + K₁, b₂₁ + K₂.

2. P₂ receives b₁₁, b₁₂, b₂₁.

3. P₃ receives b₁₂ + K₁, b₂₁ + K₂, b₂₂.

4. P₄ receives b₁₂ + 2K₁, b₂₁ + K₂, b₂₂ + K₂.

(All arithmetic is performed in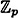

To this point, we have explained all the information in Table 11.1 except for the values of ρ* for access structures # 12 and # 13. These values arise from a more general version of the decomposition construction which we do not describe here; see the notes below.

11.9 Notes and References

Threshold schemes were invented independently by Blakley [BL79] and Shamir [SH79]. Secret sharing for general access structures was first studied in Ito, Saito, and Nishizeki [ISN87]; we based Section 11.2 on the approach of Benaloh and Leichter [BL90]. The vector space construction is due to Brickell [BR89A]. The entropy bound of Section 11.7 is proved in Capocelli et al. [CDGV93], and some of the other material from this section is found in Blundo et al. [BDSV93].

In this chapter, we have emphasized a linear-algebraic and combinatorial approach to secret sharing. Some interesting connections with matroid theory can be found in Brickell and Davenport [BD91]. Secret sharing schemes can also be constructed using geometric techniques. Simmons has done considerable research in this direction; we refer to [SI92A] for an overview of geometric techniques in secret sharing. Further discussion of these topics, as well as constructions for schemes having information rate 2/3 for access structures # 12 and # 13, can be found in the expository paper by Stinson [ST92A].

Table of Contents