Cryptography: Theory and Practice:Secret Sharing Schemes
 | Cryptography: Theory and Practice by Douglas Stinson CRC Press, CRC Press LLC ISBN: 0849385210 Pub Date: 03/17/95 |
| Previous | Table of Contents | Next |
Applying Theorem 11.5, an ideal scheme results.
Eight access structures remain to be considered. It is possible to use ad hoc applications of the vector space construction to construct ideal schemes for four of these: # 11, # 14, # 15 and # 16. We present the constructions for # 11 and # 14 here.
Example 11.8
For access structure # 11, take d = 3, p ≥ 3, and define φ as follows:
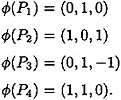
First, we have
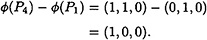
Also,
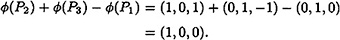
Hence,
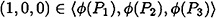
and
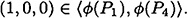
Now, it suffices to show that
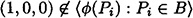
if B is a maximal unauthorized subset. There are three such subsets B to be considered: {P1, P2}, {P1, P3}, and {P2, P3, P4}. In each case, we need to establish that a system of linear equations has no solution. For example, suppose that
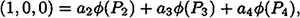
where 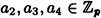 . This is equivalent to the system
. This is equivalent to the system
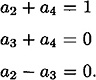
The system is easily seen to have no solution. We leave the other two subsets B for the reader to consider.
Example 11.9
For access structure # 14, take d = 3, p ≥ 2 and define φ as follows:
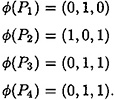
Again, Property (11.3) is satisfied and hence an ideal scheme results.
Constructions of ideal schemes for the access structures # 15 and # 16 are left as exercises. In the next section, we will show that the remaining four access structures cannot be realized by ideal schemes.
11.7 An Upper Bound on the Information Rate
Four access structures remain to be considered: # 5, # 8, # 12, and # 13. We will see in this section that in each case, there does not exist a scheme having information rate ρ > 2/3.
Denote by ρ* = ρ* (Γ) the maximum information rate for any perfect secret sharing scheme realizing a specified access structure Γ. The first result we present is an entropy bound that will lead to an upper bound on ρ* for certain access structures. We have defined a probability distribution 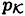 on
on  ; the entropy of this probability distribution is denoted H(K). We have also denoted by
; the entropy of this probability distribution is denoted H(K). We have also denoted by 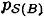 the probability distribution on the shares given to a subset
the probability distribution on the shares given to a subset 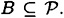 . We will denote the entropy of this probability distribution by H(B).
. We will denote the entropy of this probability distribution by H(B).
We begin by giving yet another definition of perfect secret sharing schemes, this time using the language of entropy. This definition is equivalent to Definition 11.3.
DEFINITION 11.5 Suppose Γ is an access structure and 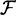 is a set of distribution rules. Then
is a set of distribution rules. Then 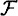 is a perfect secret sharing scheme realizing the access structure Γ provided that the following two properties are satisfied:
is a perfect secret sharing scheme realizing the access structure Γ provided that the following two properties are satisfied:
- 1. For any authorized subset of participants
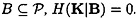
- 2. For any unauthorized subset of participants
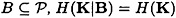 .
. - 2. For any unauthorized subset of participants
We will require several entropy identities and inequalities. Some of these results were given in Section 2.3 and the rest are proved similarly, so we state them without proof in the following Lemma.
LEMMA 11. 6
Let X, Y and Z be random variables. Then the following hold:
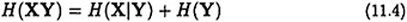
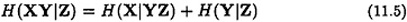
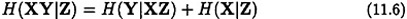



We next prove two preliminary entropy lemmas for secret sharing schemes.
LEMMA 11.7
Suppose Γ is an access structure and 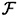 is a set of distribution rules realizing Γ.
is a set of distribution rules realizing Γ.
Suppose B ∉ Γ and 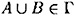 , where
, where 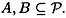 . Then
. Then

PROOF From Equations 11.5 and 11.6, we have that
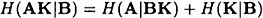
and
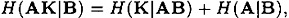
so
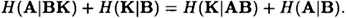
Since, by Property 2 of Definition 11.5, we have
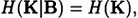
and, by Property 1 of Definition 11.5, we have
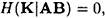
the result follows.
LEMMA 11.8
Suppose Γ is an access structure and 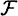 is a set of distribution rules realizing Γ. Suppose
is a set of distribution rules realizing Γ. Suppose 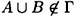 , where
, where 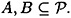 . Then H (A|B) = H (A|BK).
. Then H (A|B) = H (A|BK).
PROOF As in Lemma 11.7, we have that
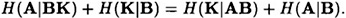
Since
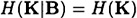
and
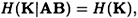
the result follows.
We now prove the following important theorem.
THEOREM 11.9
Suppose Γ is an access structure such that
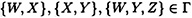
and
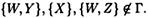
Let 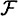 be any perfect secret sharing scheme realizing Γ. Then H (XY) ≥ 3H (K).
be any perfect secret sharing scheme realizing Γ. Then H (XY) ≥ 3H (K).
PROOF We establish a sequence of inequalities:
| H(K) | = | H(Y|WZ) - H(Y|WZK) | by Lemma 11.7 |
| ≤ | H(Y|WZ) | by (11.7) | |
| ≤ | H(Y|W) | by (11.8) | |
| = | H(Y|WK) | by Lemma 11.8 | |
| ≤ | H(XY|WK) | by (11.9) | |
| = | H(X|WK) + H(Y|WXK) | by (11.5) | |
| ≤ | H(X|WK) + H(Y|XK) | by (11.8) | |
| = | H(X|W) - H(K) + H(Y|X) - H(K) | by Lemma 11.7 | |
| ≤ | H(X) - H(K) + H(Y|X) - H(K) | by (11.7) | |
| = | H(XY) - 2H(K) | by (11.4). |
Hence, the result follows.
COROLLARY 11.10
Suppose that Γ is an access structure that satisfies the hypotheses of Theorem 11.9. Suppose the 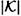 keys are equally probable. Then ρ ≤ 2/3.
keys are equally probable. Then ρ ≤ 2/3.
PROOF Since the keys are equiprobable, we have
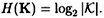
Also, we have that
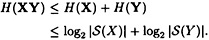
By Theorem 11.9, we have that
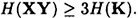
Hence it follows that
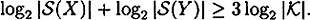
Now, by the definition of information rate, we have
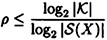
and
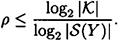
It follows that
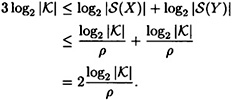
Hence, ρ ≤ 2/3.
For the access structures # 5, # 8, # 12, and # 13, the hypotheses of Theorem 11.9 are satisfied. Hence, ρ* ≤ 2/3 for these four access structures.
We also have the following result concerning ρ* in the case where the access structure has a basis Γ0 which is a graph. The proof involves showing that any connected graph which is not a multipartite graph contains an induced subgraph on four vertices that is isomorphic to the basis of access structure # 5 or # 8. If G = (V, E) is a graph with vertex set V and edge set E, and 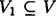 , then the induced subgraph G[V1] is defined to be the graph (V1, E1), where
, then the induced subgraph G[V1] is defined to be the graph (V1, E1), where
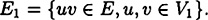
| Previous | Table of Contents | Next |
Copyright © CRC Press LLC
EAN: 2147483647
Pages: 133