Section 9.2. The RSA Algorithm
9.2. The RSA AlgorithmThe pioneering paper by Diffie and Hellman [DIFF76b] introduced a new approach to cryptography and, in effect, challenged cryptologists to come up with a cryptographic algorithm that met the requirements for public-key systems. One of the first of the responses to the challenge was developed in 1977 by Ron Rivest, Adi Shamir, and Len Adleman at MIT and first published in 1978 [RIVE78].[4] The Rivest-Shamir-Adleman (RSA) scheme has since that time reigned supreme as the most widely accepted and implemented general-purpose approach to public-key encryption.
The RSA scheme is a block cipher in which the plaintext and ciphertext are integers between 0 and n 1 for some n. A typical size for n is 1024 bits, or 309 decimal digits. That is, n is less than 21024. We examine RSA in this section in some detail, beginning with an explanation of the algorithm. Then we examine some of the computational and cryptanalytical implications of RSA. Description of the AlgorithmThe scheme developed by Rivest, Shamir, and Adleman makes use of an expression with exponentials. Plaintext is encrypted in blocks, with each block having a binary value less than some number n. That is, the block size must be less than or equal to log2(n); in practice, the block size is i bits, where 2i < n C = Me mod n M = Cd mod n = (Me)d mod n = Med mod n Both sender and receiver must know the value of n. The sender knows the value of e, and only the receiver knows the value of d. Thus, this is a public-key encryption algorithm with a public key of PU = {e, n} and a private key of PU = {d, n}. For this algorithm to be satisfactory for public-key encryption, the following requirements must be met:
For now, we focus on the first requirement and consider the other questions later. We need to find a relationship of the form Med mod n = M The preceding relationship holds if e and d are multiplicative inverses modulo f(n), where f(n) is the Euler totient function. It is shown in Chapter 8 that for p, q prime, f(pq) = (p 1)(q 1) The relationship between e and d can be expressed as Equation 9-1 This is equivalent to saying ed That is, e and d are multiplicative inverses mod f(n). Note that, according to the rules of modular arithmetic, this is true only if d (and therefore e) is relatively prime to f(n). Equivalently, gcd(f(n),d) = 1. See Appendix 9A for a proof that Equation (9.1) satisfies the requirement for RSA. We are now ready to state the RSA scheme. The ingredients are the following:
The private key consists of {d, n} and the public key consists of {e, n}. Suppose that user A has published its public key and that user B wishes to send the message M to A. Then B calculates C = Me mod n and transmits C. On receipt of this ciphertext, user A decrypts by calculating M = Cd mod n. Figure 9.5 summarizes the RSA algorithm. An example, from [SING99], is shown in Figure 9.6. For this example, the keys were generated as follows:
Figure 9.5. The RSA Algorithm Figure 9.6. Example of RSA Algorithm The resulting keys are public key PU = {7,187} and private key PR = {23,187}. The example shows the use of these keys for a plaintext input of M = 88. For encryption, we need to calculate C = 887 mod 187. Exploiting the properties of modular arithmetic, we can do this as follows: 887 mod 187 = [(884 mod 187) x (882 mod 187) x (881 mod 187)] mod 187 881 mod 187 = 88 882 mod 187 = 7744 mod 187 = 77 884 mod 187 = 59,969,536 mod 187 = 132 887 mod 187 = (88 x 77 x 132) mod 187 = 894,432 mod 187 = 11 For decryption, we calculate M = 1123 mod 187: 1123 mod 187 = [(111 mod 187) x (112 mod 187) x (114 mod 187) x (118 mod 187) x (118 mod 187)] mod 187 111 mod 187 = 11 112 mod 187 = 121 114 mod 187 = 14,641 mod 187 = 55 118 mod 187 = 214,358,881 mod 187 = 33 1123 mod 187 = (11 x 121 x 55 x 33 x 33) mod 187 = 79,720,245 mod 187 = 88 Computational AspectsWe now turn to the issue of the complexity of the computation required to use RSA. There are actually two issues to consider: encryption/decryption and key generation. Let us look first at the process of encryption and decryption and then consider key generation. Exponentiation in Modular ArithmeticBoth encryption and decryption in RSA involve raising an integer to an integer power, mod n. If the exponentiation is done over the integers and then reduced modulo n, the intermediate values would be gargantuan. Fortunately, as the preceding example shows, we can make use of a property of modular arithmetic: [(a mod n) x (b mod n)] mod n = (a x b) mod n Thus, we can reduce intermediate results modulo n. This makes the calculation practical. Another consideration is the efficiency of exponentiation, because with RSA we are dealing with potentially large exponents. To see how efficiency might be increased, consider that we wish to compute x16. A straightforward approach requires 15 multiplications: x16 = x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x However, we can achieve the same final result with only four multiplications if we repeatedly take the square of each partial result, successively forming x2, x4, x8, x16. As another example, suppose we wish to calculate x11 mod n for some integers x and n. Observe that x11 = x1+2+8 = (x)(x2)(x8). In this case we compute x mod n, x2 mod n, x4 mod n, and x8 mod n and then calculate [(x mod n) x (x2 mod n) x (x8 mod n) mod n. More generally, suppose we wish to find the value ab with a and b positive integers. If we express b as a binary number bkbk1 ... b0 then we have Therefore, We can therefore develop the algorithm[5] for computing ab mod n, shown in Figure 9.7. Table 9.3 shows an example of the execution of this algorithm. Note that the variable c is not needed; it is included for explanatory purposes. The final value of c is the value of the exponent.
Figure 9.7. Algorithm for Computing ab mod nNote: The integer b is expressed as a binary number bkbk1 ... b0
Efficient Operation Using the Public KeyTo speed up the operation of the RSA algorithm using the public key, a specific choice of e is usually made. The most common choice is 65537 (216 1); two other popular choices are 3 and 17. Each of these choices has only two 1 bits and so the number of multiplications required to perform exponentiation is minimized. However, with a very small public key, such as e = 3, RSA becomes vulnerable to a simple attack. Suppose we have three different RSA users who all use the value e = 3 but have unique values of n, namely n1, n2, n3. If user A sends the same encrypted message M to all three users, then the three ciphertexts are C1 = M3 mod n1; C2 = M3 mod n2; C3 = M3 mod n3. It is likely that n1, n2, and n3 are pairwise relatively prime. Therefore, one can use the Chinese remainder theorem (CRT) to compute M3 mod (n1n2n3). By the rules of the RSA algorithm, M is less than each of the ni therefore M3 < n1n2n3. Accordingly, the attacker need only compute the cube root of M3. This attack can be countered by adding a unique pseudorandom bit string as padding to each instance of M to be encrypted. This approach is discussed subsequently. The reader may have noted that the definition of the RSA algorithm (Figure 9.5) requires that during key generation the user selects a value of e that is relatively prime to f(n). Thus, for example, if a user has preselected e = 65537 and then generated primes p and q, it may turn out that gcd(f(n),e) Efficient Operation Using the Private KeyWe cannot similarly choose a small constant value of d for efficient operation. A small value of d is vulnerable to a brute-force attack and to other forms of cryptanalysis [WIEN90]. However, there is a way to speed up computation using the CRT. We wish to compute the value M = Cd mod n. Let us define the following intermediate results:
Following the CRT, Equation (8.8), define the quantities:
The CRT then shows, using Equation (8.9), that M = (VpXp + VqXq) mod n Further, we can simplify the calculation of Vp and Vq using Fermat's theorem, which states that ap1
The quantities d mod (P1) and d mod (q1) can be precalculated. The end result is that the calculation is approximately four times as fast as evaluating M = Cd mod n directly [BONE02]. Key GenerationBefore the application of the public-key cryptosystem, each participant must generate a pair of keys. This involves the following tasks:
First, consider the selection of p and q. Because the value of n = pq will be known to any potential adversary, to prevent the discovery of p and q by exhaustive methods, these primes must be chosen from a sufficiently large set (i.e., p and q must be large numbers). On the other hand, the method used for finding large primes must be reasonably efficient. At present, there are no useful techniques that yield arbitrarily large primes, so some other means of tackling the problem is needed. The procedure that is generally used is to pick at random an odd number of the desired order of magnitude and test whether that number is prime. If not, pick successive random numbers until one is found that tests prime. A variety of tests for primality have been developed (e.g., see [KNUT98] for a description of a number of such tests). Almost invariably, the tests are probabilistic. That is, the test will merely determine that a given integer is probably prime. Despite this lack of certainty, these tests can be run in such a way as to make the probability as close to 1.0 as desired. As an example, one of the more efficient and popular algorithms, the Miller-Rabin algorithm, is described in Chapter 8. With this algorithm and most such algorithms, the procedure for testing whether a given integer n is prime is to perform some calculation that involves n and a randomly chosen integer a. If n "fails" the test, then n is not prime. If n "passes" the test, then n may be prime or nonprime. If n passes many such tests with many different randomly chosen values for a, then we can have high confidence that n is, in fact, prime. In summary, the procedure for picking a prime number is as follows.
This is a somewhat tedious procedure. However, remember that this process is performed relatively infrequently: only when a new pair (PU, PR) is needed. It is worth noting how many numbers are likely to be rejected before a prime number is found. A result from number theory, known as the prime number theorem, states that the primes near N are spaced on the average one every (ln N) integers. Thus, on average, one would have to test on the order of ln(N) integers before a prime is found. Actually, because all even integers can be immediately rejected, the correct figure is ln(N)/2. For example, if a prime on the order of magnitude of 2200 were sought, then about ln(2200)/2 = 70 trials would be needed to find a prime. Having determined prime numbers p and q, the process of key generation is completed by selecting a value of e and calculating d or, alternatively, selecting a value of d and calculating e. Assuming the former, then we need to select an e such that gcd(f(n), e) = 1 and then calculate d The Security of RSAFour possible approaches to attacking the RSA algorithm are as follows:
The defense against the brute-force approach is the same for RSA as for other cryptosystems, namely, use a large key space. Thus, the larger the number of bits in d, the better. However, because the calculations involved, both in key generation and in encryption/decryption, are complex, the larger the size of the key, the slower the system will run. In this subsection, we provide an overview of mathematical and timing attacks. The Factoring ProblemWe can identify three approaches to attacking RSA mathematically:
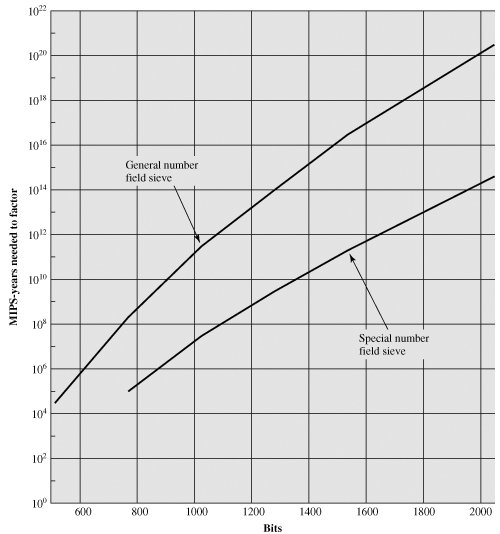
Most discussions of the cryptanalysis of RSA have focused on the task of factoring n into its two prime factors. Determining f(n) given n is equivalent to factoring n [RIBE96]. With presently known algorithms, determining d given e and n appears to be at least as time-consuming as the factoring problem [KALI95]. Hence, we can use factoring performance as a benchmark against which to evaluate the security of RSA. For a large n with large prime factors, factoring is a hard problem, but not as hard as it used to be. A striking illustration of this is the following. In 1977, the three inventors of RSA dared Scientific American readers to decode a cipher they printed in Martin Gardner's "Mathematical Games" column [GARD77]. They offered a $100 reward for the return of a plaintext sentence, an event they predicted might not occur for some 40 quadrillion years. In April of 1994, a group working over the Internet claimed the prize after only eight months of work [LEUT94]. This challenge used a public key size (length of n) of 129 decimal digits, or around 428 bits. In the meantime, just as they had done for DES, RSA Laboratories had issued challenges for the RSA cipher with key sizes of 100, 110, 120, and so on, digits. The latest challenge to be met is the RSA-200 challenge with a key length of 200 decimal digits, or about 663 bits. Table 9.4 shows the results to date. The level of effort is measured in MIPS-years: a million-instructions-per-second processor running for one year, which is about 3 x 1013 instructions executed. A 1 GHz Pentium is about a 250-MIPS machine.
A striking fact about Table 9.4 concerns the method used. Until the mid-1990s, factoring attacks were made using an approach known as the quadratic sieve. The attack on RSA-130 used a newer algorithm, the generalized number field sieve (GNFS), and was able to factor a larger number than RSA-129 at only 20% of the computing effort. The threat to larger key sizes is twofold: the continuing increase in computing power, and the continuing refinement of factoring algorithms. We have seen that the move to a different algorithm resulted in a tremendous speedup. We can expect further refinements in the GNFS, and the use of an even better algorithm is also a possibility. In fact, a related algorithm, the special number field sieve (SNFS), can factor numbers with a specialized form considerably faster than the generalized number field sieve. Figure 9.8 compares the performance of the two algorithms. It is reasonable to expect a breakthrough that would enable a general factoring performance in about the same time as SNFS, or even better [ODLY95]. Thus, we need to be careful in choosing a key size for RSA. For the near future, a key size in the range of 1024 to 2048 bits seems reasonable. Figure 9.8. MIPS-years Needed to Factor |
X | = (C mod n) x (2e mode n) |
= (Me mod n) x (2e mode n) | |
= (2M)e mod n |
Therefore, Y = (2M) mod n From this, we can deduce M. To overcome this simple attack, practical RSA-based cryptosystems randomly pad the plaintext prior to encryption. This randomizes the ciphertext so that Equation (9.2) no longer holds. However, more sophisticated CCAs are possible and a simple padding with a random value has been shown to be insufficient to provide the desired security. To counter such attacks RSA Security Inc., a leading RSA vendor and former holder of the RSA patent, recommends modifying the plaintext using a procedure known as optimal asymmetric encryption padding (OAEP). A full discussion of the threats and OAEP are beyond our scope; see [POIN02] for an introduction and [BELL94a] for a thorough analysis. Here, we simply summarize the OAEP procedure.
Figure 9.9 depicts OAEP encryption. As a first step the message M to be encrypted is padded. A set of optional parameters P is passed through a hash function H.[6] The output is then padded with zeros to get the desired length in the overall data block (DB). Next, a random seed is generated and passed through another hash function, called the mask generating function (MGF). The resulting hash value is bit-by-bit XORed with DB to produce a maskedDB. The maskedDB is in turn passed through the MGF to form a hash that is XORed with the seed to produce the masked seed. The concatenation of the maskedseed and the maskedDB forms the encoded message EM. Note that the EM includes the padded message, masked by the seed, and the seed, masked by the maskedDB. The EM is then encrypted using RSA.
[6] A hash function maps a variable-length data block or message into a fixed-length value called a hash code. Hash functions are discussed in depth in Chapters 11 and 12.
Figure 9.9. Encryption Using Optimal Assymetric Encryption Padding (OAEP)

EAN: 2147483647
Pages: 209
 2
2 1 mod
1 mod 



 1, Thus, the user must reject any value of
1, Thus, the user must reject any value of