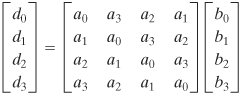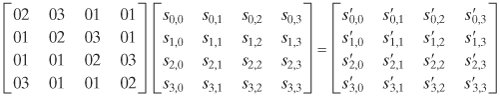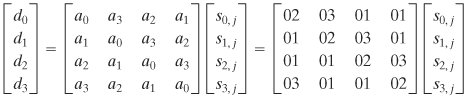Appendix 5A Polynomials with Coefficients in GF(28)

[Page 163]

Appendix 5A Polynomials with Coefficients in GF(2⁸)

In Section 4.5, we discussed polynomial arithmetic in which the coefficients are in Z_p and the polynomials are defined modulo a polynomial M(x) whose highest power is some integer n. In this case, addition and multiplication of coefficients occurred within the field Z_p; that is, addition and multiplication were performed modulo p.

The AES document defines polynomial arithmetic for polynomials of degree 3 or less with coefficients in GF(2⁸). The following rules apply:

1. Addition is performed by adding corresponding coefficients in GF(2⁸). As was pointed out Section 4.5, if we treat the elements of GF(2⁸) as 8-bit strings, then addition is equivalent to the XOR operation. So, if we have

   Equation 5-8

   

   
   

   Equation 5-9

   

   
   

   then

   a(x) + b(x) = (a₃ x³ + (a² x² + (a₁ x + (a₀

   Multiplication is performed as in ordinary polynomial multiplication, with two refinements:

   1. Coefficients are multiplied in GF(2⁸).

   2. The resulting polynomial is reduced mod (x⁴ + 1).

We need to keep straight which polynomial we are talking about. Recall from Section 4.6 that each element of GF(2⁸) is a polynomial of degree 7 or less with binary coefficients, and multiplication is carried out modulo a polynomial of degree 8. Equivalently, each element of GF(2⁸) can be viewed as an 8-bit byte whose bit values correspond to the binary coefficients of the corresponding polynomial. For the sets defined in this section, we are defining a polynomial ring in which each element of this ring is a polynomial of degree 3 or less with coefficients in GF(2⁸), and multiplication is carried out modulo a polynomial of degree 4. Equivalently, each element of this ring can be viewed as a 4-byte word whose byte values are elements of GF(2⁸) that correspond to the 8-bit coefficients of the corresponding polynomial.

We denote the modular product of a(x) and b(x) by a(x) x). To compute d(x) = a(x) x), the first step is to perform a multiplication without the modulo operation and to collect coefficients of like powers. Let us express this as c(x) = a(x) x b(x) Then

Equation 5-10

where

c₀ = a₀ · b₀

c₁ = (a1 · b₀) (b₁)

c₂ = (a2 · b₀) (b₁) (b₂)

c₃ = (a3 · b₀) (b₁) (b₂) (b₃)

c₄ = (a₃ · b₁) (b₂) (b₃)

c₅ = (a₃ · b₂) (b₃)

c₆ = (a₃ · b₃)

The final step is to perform the modulo operation:

d(x) = c(x) mod (x⁴ + 1)

That is, d(x) must satisfy the equation

c(x) = [(x⁴ + 1) x q(x)] x)

such that the degree of d(x) is 3 or less.

---

[Page 164]

A practical technique for performing multiplication over this polynomial ring is based on the observation that

Equation 5-11

If we now combine Equations (5.10) and (5.11), we end up with

d(x) = c(x) mod (x⁴ + 1) = [c₆x⁶ + c₅x⁵ + c₄x⁴ + c₃x³ + c₂x² + c₁x + c₀] mod (x⁴ + 1)

= c₃x³ + (c₂ x² + (c₁ x + (c₀ Expanding the c_i coefficients, we have the following equations for the coefficients of d(x):

d₀ = (a₀ · b₀) (b₁) (b₂) (b₃)

d₁ = (a₁ · b₀) (b₁) (b₂) (b₃)

d₂ = (a₂) · b₀) (b₁) (b₂) (b₃)

d₃ = (a₃ · b₀) (b₁) (b₂) (b₃)

This can be written in matrix form:

Equation 5-12

MixColumns Transformation

In the discussion of MixColumns, it was stated that there were two equivalent ways of defining the transformation. The first is the matrix multiplication shown in Equation (5.3), repeated here:

The second method is to treat each column of State as a four-term polynomial with coefficients in GF(2⁸). Each column is multiplied modulo (x⁴ + 1) by the fixed polynomial a(x), given by

a(x = {03}x³ + {01}x² + {01}x + {02}

From Equation (5.8), we have a₃ = {03}; a₂ = {01}; a₀ = {02}. For the jth column of State, we have the polynomial col_j(x) = s_3,jx³ + s_2,jx² + s_1,jx + s_0,j. Substituting into Equation (5.12), we can express d(x) = a(x) x col_j(x) as

which is equivalent to Equation (5.3).

Multiplication by x

Consider the multiplication of a polynomial in the ring by x: c(x) = x x). We have

c(x) = x x) = [x x (b₃x³) + b₂x² + b₁x + b₀)] mod (x⁴ + 1)

---

[Page 165]

= (b₃x⁴ + b₂x³ + b₁x² + b₀x) mod (x⁴ + 1)

= b₂x³ + b₁x² + b₀x + b₃

Thus, multiplication by x corresponds to a 1-byte circular left shift of the 4 bytes in the word representing the polynomial. If we represent the polynomial as a 4-byte column vector, then we have