7.1 Measurement fundamentals
7.1 Measurement fundamentals
Measuring is not easy. First is the question of the validity and reliability of the measurements. Second is the dilemma of which scale to choose to represent the data captured. Third is the problem of relating these measurements to other measurements. Fourth is the difficulty of aggregating or summarizing the measurements to describe and make inferences about the processes' capabilities. Fifth is the fact that by defining measurements, we are defining what we regard as important, otherwise why would we measure it? And this simple implication might distort the measurements we collect, due to the general tendency of people to put themselves and their projects in the best possible light.
7.1.1 Validity and reliability
For measurements to be useful, they need to be valid and reliable. A valid measurement is one that actually measures what it claims to measure. An example of a common invalid measurement is the number of hours spent as a proxy for progress. A reliable measurement is one that will give you or anyone else approximately the same value when taken on the same object or individual. The commonly used "percentage complete" measurement is highly unreliable because it depends on the opinion of an individual regarding how much work was done and the relative effort required by whatever work is left.
The type of validity to which we referred above is called construct validity and it is of course fundamental to any measurement activity, but the fact that the metric reflects the concept that we want to measure alone does not make it a useful metric. There are other types of validity that need to be verified in order to select metrics that can be relied on for decision-making purposes. These validity types are predictive validity, which is the ability of the metric to be used for estimating and forecasting purposes, discriminant validity, which refers to the ability of the metric to distinguish between things that are different, and content validity, which refers to the extent to which the measure covers all the meanings included in the attribute being measured.
Reliability refers to the consistency of a number of measurements taken using the same measurement method. If the measurements yield approximately the same value, the measurement is reliable. If the variations among them are large, the reliability is low. The reliability of a measurement is influenced by the quality of its definition; vague definitions are likely to result in unreliable measurements, by the measurement instrument and even by the reporting routines.
7.1.2 Levels of measurement
The data used to manage projects or to improve processes is the result of a measurement process that maps the attributes of a task, deliverable, or other relevant entities into a well-defined scale.
The reason for bringing up the topic of scales types, also called measurement levels since the information content associated with each of them differs, is twofold. First, relevant relationships that might exist between objects in the "real world" could be lost in the process of measurement if the scale selected does not possess certain properties. Second, depending on the type of scale selected it would be possible to apply certain transformations like adding, subtracting, or averaging to the measured values and to infer a number of conclusions but not others. In summary, the choice of scale limits the type of information that we can extract from the data collected.
Scales are classified according to whether or not they have the properties of magnitude, equal intervals, and absolute zero [2]. When a scale has magnitude, one instance of the attribute being measured can be judged greater than, less than, or equal to another instance of the attribute. When a scale possesses the property of equal intervals, the distance between consecutive values of the attribute is the same regardless of where in the scale they fall. An absolute zero is a value that indicates that nothing of the attribute being measured exists.
Based on these properties, four types of measurement scales or measurement levels are commonly distinguished: nominal, ordinal, interval, and ratio.
In a nominal scale, the measurement values are categories(i.e., they do not have magnitude). For example, the classification of defects in a software project according to their source does not imply an order among them (i.e., it does not make sense to say that the category "requirements" is less than the category "Coding," this even if the categories were labeled "1" and "2," respectively). When the results of a measurement are expressed in a nominal scale, the type of analysis and summarization that we can do is reduced to counting and establishing proportions among the categories. For a nominal scale, the only measure of central tendency that makes sense is the mode, that is the category with the most occurrences.
Next in the hierarchy of measurements are the ordinal scales. Next means that all operations and transformations applicable to a nominal scale are also applicable to an ordinal scale. An ordinal scale has the property of magnitude, so it is possible to rank objects and arrange them in ascending (or descending) order; however, since an ordinal scale has neither the equal intervals nor the absolute-zero properties, the distances between the values have no meaning. The classification of change requests according to priorities such as "1", "2", and "3", where the ones labeled "1" are more urgent than those labeled "2" and those labeled "2" are more important than those labeled "3", is an example of an ordinal scale. Statements, such as "The average priority for these changes is 2.3" or "a priority 1 request is twice as important as a priority 2 request", however, are inconsistent with the use of an ordinal scale. For ordinal scales, we can use the mode or the median as a measure of central tendency and percentiles as a measure of dispersion.
Next come the interval and the ratio scales. These two scales possess both magnitude and equal intervals. The difference between them is that the ratio scale has an absolute-zero point and the interval scale does not. The classic examples of interval scales are the Celsius and Fahrenheit scales, in which a temperature of 0 degrees does not mean that there is no temperature at all, only that the temperature at that point is colder than a temperature of 10 degrees by a difference of 10 degrees. So in the case of an interval scale, saying that a temperature of 20 degrees is twice as hot as a temperature of 10 degrees would be totally misleading. Imagine that we equate the concept of "warmth" with values on the Celsius scale, and suppose that one Monday we measure a temperature of 10 degrees. If the temperature drops to 1 degree Celsius on Tuesday, was it really ten times as warm on Monday? What if the temperature drops to 0.1 degree Celsius on Wednesday? Was it 10 times as warm on Tuesday, and 100 times as warm on Monday? Clock times, calendar dates, and normalized intelligence scores are examples of frequently used measures from interval scales. The arithmetic mean is the typical measure of central tendency and the standard deviation the measure of the dispersion.
With a true origin or absolute-zero point, division and multiplication become meaningful in the case of ratio scales and all the mathematical operations that we customarily use for real numbers are legitimate. Cost, schedule length, and time between failures are examples of ratio scales. In addition to the operations valid for the interval scales, ratio scales allow for geometric mean, harmonic mean, and percent variation.
7.1.3 Measures of dispersion as an expression of risk
Should we decide to measure productivity, or for that matter any other attribute, in a number of projects we would find that seldom would two of them yield the same number. The reason for this is that behind a simple ratio between the output and the input, there are hidden many circumstances such as people abilities and motivation, task difficulty, undocumented interruptions, scope changes, and external factors that influence the measurement and that cannot be accounted for or separated from the measurements themselves. The more of these special circumstances there are and the greater their influence, the greater the difference will be among measured values (see Figure 7.2).
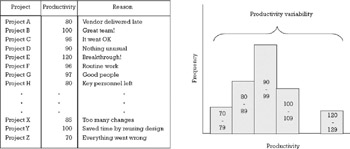
Figure 7.2: Variability present in measurements due to uncontrollable factors.
When this data is used to compute project durations or the effort needed, this variability will be passed on to the plans, and obviously, the higher the variability the higher the risk. Similarly, the assumptions we made about the project being planned will result in added uncertainty.
In interval and ratio scales, this variability is quantitatively expressed by the standard deviation of the set of values, and in consequence the larger the standard deviation, the higher the risk. Other measures of dispersion, such as the range and the percentiles of a distribution, will, although less effectively, also express the degree of uncertainty associated with a set of measurements.
7.1.4 Relationships between measurement variables
After you have been measuring for a while, certain patterns will start to emerge. Some conditions always seem to lead to the same results, and although they might fail from time to time, they become rather predictable. You might even be tempted to postulate a few theories of your own about how things work or to conjecture the existence of some relationships between a pair of measurements and use them to make decisions.
A scatter plot (see Figure 7.3) is a useful tool to reveal a relationship or association between two measurement variables. Such relationships manifest themselves by any nonrandom structure in the plot.
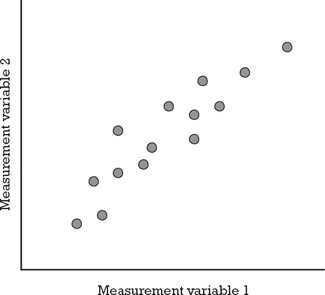
Figure 7.3: Scatter plot showing the relationship between two measurement values.
Scatter plots can provide answers to the following questions:
-
Are variables X and Y related?
-
Are variables X and Y linearly related?
-
Are variables X and Y nonlinearly related?
-
Does the variation in Y change depending on X?
-
Are there outliers?
Various common types of patterns are demonstrated by the examples in Figure 7.4.
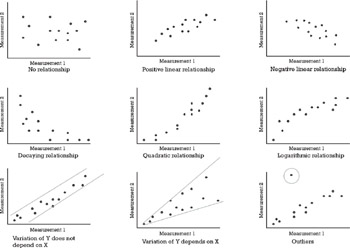
Figure 7.4: Relationships between measurement variables: typical patterns.
When there is a relationship between two measurement variables, the variables are called correlated; when there is no relationship, they are called independent. The fact that two variables are correlated does not imply that they are causally connected; sometimes the two variables could be connected through a third one that makes them move in the same direction at the same time. Take the case of effort and schedule in projects—are they correlated? Or is it scope that drives both cost and schedule? Should we fix the scope, what would be more expensive: a project with a compressed schedule or one with a normal schedule? In other cases there is a third variable, called a confounding variable, whose effects on the response variable cannot be separated from those of the explanatory variable. For example, in a recent study [3], only four out of 24 commonly used object-oriented metrics were actually useful in predicting the quality of a software module when the effect of the module size was accounted for. Yet another common problem could be the presence of outliers in the data, which tends to inflate the strength of a relationship. These problems are illustrated in Figure 7.5.
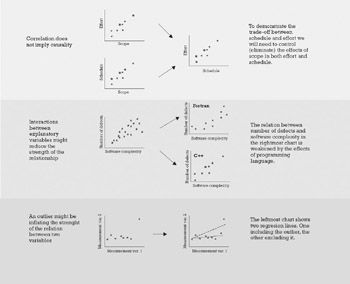
Figure 7.5: Common problems in the analysis of relationships.
7.1.5 Aggregating measurements
Measurement data is usually generated at relatively low levels of detail within projects. For example, worked hours are usually collected at the work package or task level; similarly, weight and power consumption are properties measured at the module or assembly level, so in order to create a consolidated picture of the whole project or product for analysis and reporting purposes, it is necessary to aggregate or summarize the primitive measurements across different aggregation structures (see Figure 7.6).
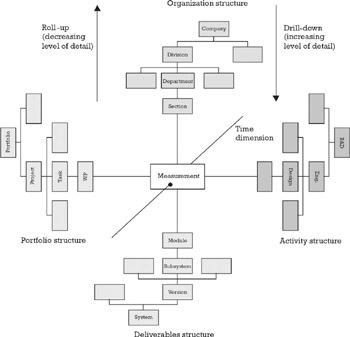
Figure 7.6: Aggregation patterns: Measurements including time report must be available at different levels of aggregation and along the time dimension.
The multiproject environment requires the use of one or more of the following aggregation structures, either in their pure form or in combinations with each other, for summarization purposes:
-
Portfolio: Data is aggregated across projects into a single element, which represents the totality of the projects, or into a hierarchy of intermediate elements representing each of the particular subsets of the total portfolio. In an R&D organization subsets of the portfolio could be established based on product lines, in technology, in risk or according to project categories such as technology development, platform development, new application development, application extension, fixes, and so on. This type of aggregation is useful to balance the project mix.
-
Organization: Data is aggregated across the organizational hierarchy mainly for responsibility accounting and resource planning purposes. The structure of this hierarchy will resemble the structure of cost centers and available capacity will be maintained for each of them.
-
Project: Data is aggregated across project activities and or deliverables to provide a consolidated view of what is going on in the project. This is the type of information typically contained in a progress report.
-
Deliverables: These structures are derived from the relationship of the system components within a particular architecture or design. This structure and the project structure are usually integrated through the project WBS.
-
Activity: These structures are based on a hierarchy of standardized life-cycle activities that cover the complete activity structure for a project and include tasks such as requirements analysis, design, implementation, integration, and test. This type of aggregation supports activity-based costing (ABC) and activity-based management (ABM) and is critical in capturing historical data for estimation and process improvement purposes.
Collectively, the aggregation structures should cover the full spectrum of projects, activities, and deliveries so that every elemental measurement can find its place in the structure, and the intersection between any two of their subsets should be empty to prevent double counting of the same value.
When using aggregated data, there is always the risk that negative variances in one element of the hierarchy could be offset by positive ones in another element, and with everything looking right at the aggregation point, we could be disregarding valuable information about what is happening deep down into the hierarchy. To prevent this, the aggregation processes need to include at least two controls: a measure of the dispersion of the underlying values and a threshold associated with the variances allowable for each element in the aggregation structure.
As the standard deviation of a variable could be used as a quantification of the risk or uncertainty associated with a given variable, it is important to understand what happens to it through the aggregation process. The first thing that needs to be looked at when adding variables is whether there is any relationship between them or if they are independent from a statistical point of view. This is important for two reasons: First, the sum of independent variables yields a much lower risk than the sum of related variables.
In Figure 7.7 we can see that the standard deviation of the sum of 25 fully correlated variables is five times larger than the standard deviation of the sum of the same variables under the assumption that they are independent. The second reason it is important is that the shape of the distribution will be affected as well. If the variables being aggregated are independent, the shape of the resulting distribution will approach that of a bell-shaped distribution regardless of the shape of the individual distributions. If the variables are correlated, the shape of the sum will instead depend on the shape of the individual distributions and on the strength and nature of their relationship. The reason this happens is simply that when variables are correlated their values tend to move in the same direction at the same time, while in the case of independent variables, the result of this independence is that some values will go up while others go down, and they cancel each other. In practical terms, the assumption of independence is expressed in the belief that the lateness of some tasks is compensated for by the early completion of others and that in the end everything balances out.

Figure 7.7: Relationship between the number of elements summed, the coefficient of correlation, and the standard deviation of the sum.
This might seem like an academic discussion for some, but it is not difficult to encounter correlated variables in development projects. For example, the underestimation of the system's complexity or the overestimation of the development team productivity will affect the duration of most tasks in the same direction. Thus, if you can think of an underlying cause capable of swinging the measurement values in the same direction, the variables are not independent but correlated, and ignoring this is perhaps one of the most costly mistakes a project manager can make.
7.1.6 Time series
A time series is a chronological sequence of measurements or observations. In a project environment, time series are very important because there is as much information contained in the timing of the measurement as there is in its magnitude. As an example, suppose that, as shown in Figure 7.8, while testing a software system we observe the same number of errors twice, one at the beginning of testing and the other near its end. At the beginning of testing one would expect the results of the next measurement to be larger as we climb through the learning curve and modules are being released for testing. For the second observation, one would expect the following readout to be smaller, as there are no new modules coming in and it is becoming increasingly difficult to find new errors.
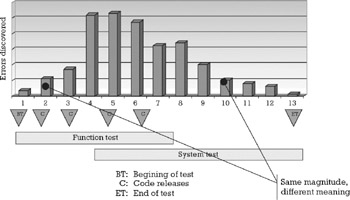
Figure 7.8: Timing of the measurement contains as much information as its magnitude.
The information contained in the time dimension of the measurements is key to the understanding of the process underlying the observed data and this knowledge is essential to the creation of forecasting models. As an example of the practical application of the knowledge gained through the study of time series, take a look at the production data in Figure 7.9. In the three illustrations contained in the picture, we can see that progress does not occur at a constant rate and that it more closely resembles the shape of Figure 7.10. This "S" pattern, typical of many intellectual activities, can be explained by the existence of a number of actions and thought processes at the beginning and end of the task which, although value adding, do not contribute directly to the output being measured, be it number of newly detected problems, thousands of lines of code, or pages written. This knowledge in turn can be used to forecast the completion date of a task more accurately than a linear extrapolation derived from the rate of progress observed through the half-life of the task. In Figure 7.10, production does not grow at a constant rate. At the peak of productivity, between weeks 3 and 5, the percentage complete soars 20% in just 1 week. Toward the end of the task it takes triple the time to go from 80% to 100% complete. Figure 7.11 shows the error incurred by using a linear forecast instead of the S-curve paradigm. Assuming that the task output is 250 units of production (requirements, FP, errors detected, etc.), a linear projection would forecast its completion by week 7.5 while the S curve would put it at week 9. Assuming that the task duration was originally estimated to be 7 weeks, according to the linear projection it will be completed on time, but according to the S curve it will be 2 weeks late.
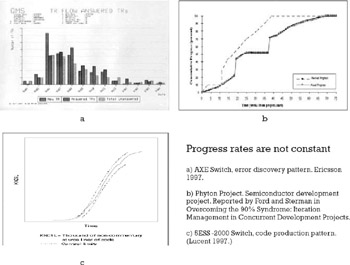
Figure 7.9: Progress, measured in terms of its visible output, is not constant through the duration of a task or project.
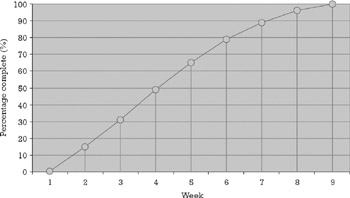
Figure 7.10: The S curve.
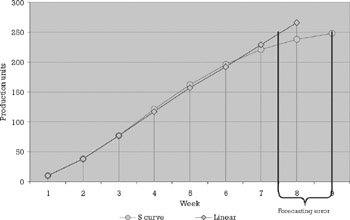
Figure 7.11: Error incurred by using linear forecast instead of S curve.
7.1.7 Sources of data
Obviously, the source of the measurement data will depend on what is being measured; however, it is possible to identify a number of important sources of data in a project environment. These are the time-reporting system, the version control or document management system, and the troubleor defect-reporting system. The importance of these sources resides not only in the wealth of information they can provide, but also in the fact that they are readily available in most organizations.
By appropriately codifying the hours reported, the time reported could be used to measure cost, staffing rates, cost of quality, staff disposition, and organization sustainability. Similarly, the version control or document management system can be supplemented with "probes" or scripts to measure changes in documents or code every time an artifact is checked in or out. The trouble-reporting system is also an extremely valuable source of information, not only with respect to the number of defects reported, but in terms of the rates at which problems are discovered and fixed.
7.1.8 Intrusive nature of measurement
Measuring performance does in fact influence performance. Peter Drucker [4] has stated that performance measurement in a social system is neither objective nor neutral. Implicitly, performance measures are a reflection of what the organization considers important; if quality is not measured, quality must not be important. This can lead to the unintended consequence of maximizing certain parameters of the organization at the expense of other equally important but much less visible parameters. Examples of unintended consequences include cutting of quality activities to meet a deadline, knowing that the work will have to be redone, at least partially, after the deadline is passed; running shorter test sequences to show a diminishing number of new trouble reports (TRs); and recording expenses as capital expenditures.
Another risk is that when organizations put too much emphasis on measurement for performance purposes, maximizing the measurements might become a substitute for achieving the goals. The way to prevent these unintended consequences is by explaining the purpose of measuring and by not having immediate payoffs linked to achieving certain performance targets and by avoiding as much as possible the use of proxy or indirect measurements instead of direct ones.
EAN: 2147483647
Pages: 81