5.7 Newton s Algorithm

---

 

	Java Number Cruncher: The Java Programmer's Guide to Numerical Computing By Ronald  Mak
	Table of Contents
	Chapter  5.   Finding Roots

---

5.7 Newton's Algorithm

Let's take another look at the iteration formula for the secant algorithm:

Suppose the function f is differentiable (and hence continuous) over the interval [ x _{n - 1} , x _n ]:

By making x _{n - 1} be the same point as x _n , we can replace the slope of the secant by the slope of the tangent at x _n , and then we have the formula for Newton's algorithm: ^[3]

^[3] Sir Isaac Newton (1643 §C1727) was an English scientist, astronomer , and mathematician who is famous for his work on optics, his laws of motion and of gravitation, his development of the calculus, and his book Principia, published in 1687. We shall encounter Newton again in Chapters 6 and 7.

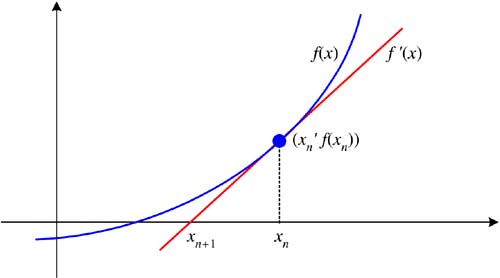
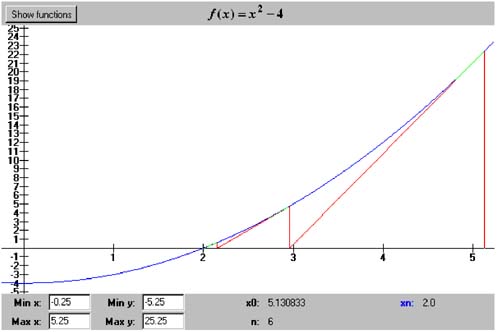
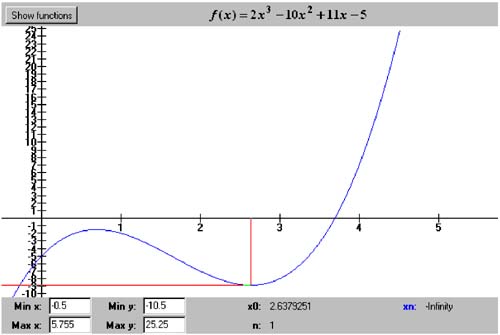
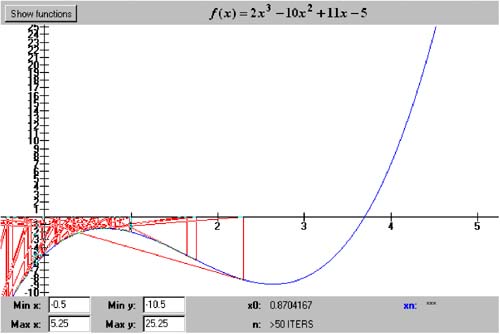
Figure 5-2 makes this clear. We draw the tangent line through the point ( x _n , f ( x _n )). The tangent line intercepts the x axis at x _{n + 1} , which is closer to the root than x _n .

Figure 5-2. One iteration step of Newton's algorithm. The tangent line is at ( x _n , f ( x _n )).

Listing 5-5a shows class NewtonsRootFinder , which implements Newton's algorithm. Notice that it invokes the derivativeAt() method of a Function object in order to evaluate a function's derivative.

Listing 5-5a The class that implements Newton's algorithm.

 package numbercruncher.mathutils; /**  * The root finder class that implements Newton's algorithm.  */ public class NewtonsRootFinder extends RootFinder {     private static final int   MAX_ITERS = 50;     private static final float TOLERANCE = 100*Epsilon.floatValue();     /** x[n] value */             private float xn;     /** x[n+1] value */           private float xnp1;     /** previous x[n+1] value */  private float prevXnp1;     /** f(x[n]) */                private float fn;     /** f(x[n+1]) */              private float fnp1;     /** f'(x[n]) */               private float fpn;     /**      * Constructor.      * @param function the functions whose roots to find      */     public NewtonsRootFinder(Function function)     {         super(function, MAX_ITERS);     }     /**      * Reset.      * @param x0 the initial x-value      */     public void reset(float x0)     {         super.reset();         xnp1 = x0;         fnp1 = function.at(xnp1);     }     //CCCCCCCCC//     // Getters //     //CCCCCCCCC//     /**      * Return the current value of x[n].      * @return the value      */     public float getXn() { return xn; }     /**      * Return the current value of x[n+1].      * @return the value      */     public float getXnp1() { return xnp1; }     /**      * Return the current value of f(x[n]).      * @return the value      */     public float getFn() { return fn; }     /**      * Return the current value of f(x[n+1]).      * @return the value      */     public float getFnp1() { return fnp1; }     /**      * Return the current value of f'(x[n]).      * @return the value      */     public float getFpn() { return fpn; }     //-----------------------------//     // RootFinder method overrides //     //-----------------------------//     /**      * Do Newton's iteration procedure.      * @param n the iteration count      */     protected void doIterationProcedure(int n)     {         xn = xnp1;     }     /**      * Compute the next position of x[n+1].      */     protected void computeNextPosition()     {         fn  = fnp1;         fpn = function.derivativeAt(xn);         // Compute the value of x[n+1].         prevXnp1 = xnp1;         xnp1     = xn - fn/fpn;         fnp1 = function.at(xnp1);     }     /**      * Check the position of x[n+1].      * @throws PositionUnchangedException      */     protected void checkPosition()         throws RootFinder.PositionUnchangedException     {         if (xnp1 == prevXnp1) {             throw new RootFinder.PositionUnchangedException();         }     }     /**      * Indicate whether or not the algorithm has converged.      * @return true if converged, else false      */     protected boolean hasConverged()     {         return Math.abs(fnp1) < TOLERANCE;     } } 

Program 5 §C5 instantiates a NewtonsRootFinder object. Screen 5-5a is a screen shot of the interactive version of the program, which allows you to dynamically set the value of the starting point x by dragging the mouse along the x axis. It animates the algorithm by tracing the algorithm's path toward the root. At x and each subsequent value of x, the program draws the vertical line from the x axis to f ( x ) and the tangent line at f ( x ). Where the tangent crosses the x axis is the next value of x. The iterations stop when f ( x ) is sufficiently close to zero.

Screen 5-5a. Newton's algorithm applied to the function f ( x ) = x ² - 4 with the initial value x = 5.130833. The vertical lines mark the values of x , and the slanted lines are the tangents at f ( x ). This screen shot is from the interactive version of Program 5 §C5.

The noninteractive version of Program 5 §C5 shows that, if we pick a good starting value x , Newton's algorithm can have a very good convergence rate. See Listing 5-5b. Actually, the algorithm has the best convergence rate of all the algorithms we've looked at so far. Once it starts to converge to a root, the number of correct significant digits in the approximation doubles with each iteration. But one drawback is that it requires the computation of the function's derivative. This may be expensive, or not even possible, for some functions.

Listing 5-5b The noninteractive version of Program 5 §C5 applies Newton's algorithm applied to the function f ( x ) = x ² - 4 with the initial value x = 5.130833.

 package numbercruncher.program5_5; import numbercruncher.mathutils.Function; import numbercruncher.mathutils.NewtonsRootFinder; import numbercruncher.mathutils.AlignRight; import numbercruncher.rootutils.RootFunctions; /**  * PROGRAM 5C5: Newton's Algorithm  *  * Demonstrate Newton's Algorithm on a function.  */ public class NewtonsAlgorithm {     /**      * Main program.      * @param args the array of runtime arguments      */     public static void main(String args[])     {         try {             NewtonsRootFinder finder =                 new NewtonsRootFinder(RootFunctions.function("x^2 - 4"));             finder.reset(5.130833f);             AlignRight ar = new AlignRight();             ar.print("n", 2);             ar.print("x[n]", 11); ar.print("f(x[n])", 14);             ar.print("f'(x[n])", 11); ar.print("x[n+1]", 11);             ar.print("f(x[n+1])", 14);             ar.underline();             // Loop until convergence or failure.             boolean converged;             do {                 converged = finder.step();                 ar.print(finder.getIterationCount(), 2);                 ar.print(finder.getXn(), 11);                 ar.print(finder.getFn(), 14);                 ar.print(finder.getFpn(), 11);                 ar.print(finder.getXnp1(), 11);                 ar.print(finder.getFnp1(), 14);                 ar.println();             } while (!converged);             System.out.println("\nSuccess! Root = " + finder.getXnp1());         }         catch(Exception ex) {             System.out.println("***** Error: " + ex);         }     } } 

Output:

 n       x[n]       f(x[n])   f'(x[n])     x[n+1]     f(x[n+1]) ---------------------------------------------------------------  1   5.130833     22.325449  10.261666   2.955217      4.733307  2   2.955217      4.733307   5.910434  2.1543777     0.6413431  3  2.1543777     0.6413431  4.3087554  2.0055313   0.022155762  4  2.0055313   0.022155762  4.0110626  2.0000076  3.0517578E-5  5  2.0000076  3.0517578E-5  4.0000153        2.0           0.0 Success! Root = 2.0 

Because of the derivative f ', we need to be extra careful when applying Newton's algorithm. The screen shots in Screen 5-5b show what can happen if the derivative f '( x ) = 0. The approximations to the root can shoot off to infinity, or they may oscillate and fail to converge.

Screen 5-5b. Pathological behavior of Newton's algorithm when the function derivative f '( x ) = 0.

---

Top