5.6 The Secant Algorithm

---

 

	Java Number Cruncher: The Java Programmer's Guide to Numerical Computing By Ronald  Mak
	Table of Contents
	Chapter  5.   Finding Roots

---

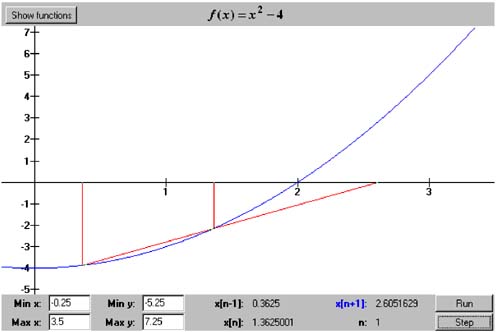
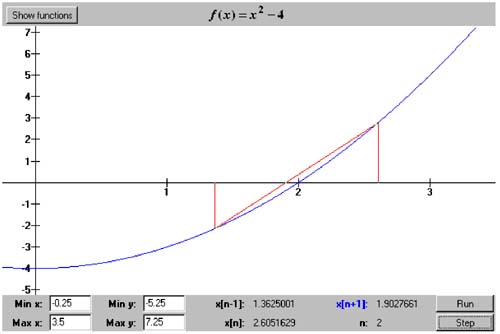
5.6 The Secant Algorithm

Unlike the bracketing bisection and regula falsi algorithms, the secant algorithm is our first example of an open algorithm, which does not work with ever shrinking intervals. It begins with two arbitrarily chosen values x and x ₁ , and for the first iteration, it draws the secant through ( x , f ( x )) and ( x ₁ , f ( x ₁ )). The next false position is x ₂ , where the secant crosses the x axis. For the next iteration, it draws the secant through ( x ₁ , f ( x ₁ )) and ( x ₂ , f ( x ₂ )) to obtain the next false position x ₃ . Each subsequent iteration n proceeds similarly, using the x _{n - 1} and x _n to obtain x _{n + 1} . Because this is an open algorithm, f ( x _{n - 1} ) and f ( x _n ) do not need to have opposite signs. The iterations continue until f ( x _{n + 1} ) is sufficiently close to 0, and then x _{n + 1} is the root.

As we did for the regula falsi algorithm, we use similar triangles to compute x _{n + 1} :

Class SecantRootFinder , shown in Listing 5-4a, implements the secant algorithm.

Listing 5-4a The class that implements the secant algorithm.

 package numbercruncher.mathutils; /**  * The root finder class that implements the secant algorithm.  */ public class SecantRootFinder extends RootFinder {     private static final int   MAX_ITERS = 50;     private static final float TOLERANCE = 100*Epsilon.floatValue();     /** x[n-1] value */              private float xnm1;     /** x[n] value */                private float xn;     /** x[n+1] value */              private float xnp1 = Float.NaN;     /** previous value of x[n+1] */  private float prevXnp1;     /** f(x[n-1]) */                 private float fnm1;     /** f([n]) */                    private float fn;     /** f(x[n+1]) */                 private float fnp1;     /**      * Constructor.      * @param function the functions whose roots to find      * @param x0 the first initial x-value      * @param x1 the second initial x-value      */     public SecantRootFinder(Function function, float x0, float x1)     {         super(function, MAX_ITERS);         // Initialize x[n-1], x[n], f(x[n-1]), and f(x[n]).         xnm1 = x0;  fnm1 = function.at(xnm1);         xn   = x1;  fn   = function.at(xn);     }     //---------//     // Getters //     //---------//     /**      * Return the current value of x[n-1].      * @return the value      */     public float getXnm1() { return xnm1; }     /**      * Return the current value of x[n].      * @return the value      */     public float getXn() { return xn; }     /**      * Return the current value of x[n+1].      * @return the value      */     public float getXnp1() { return xnp1; }     /**      * Return the current value of f(x[n-1]).      * @return the value      */     public float getFnm1() { return fnm1; }     /**      * Return the current value of f(x[n]).      * @return the value      */     public float getFn() { return fn; }     /**      * Return the current value of f(x[n+1]).      * @return the value      */     public float getFnp1() { return fnp1; }     //-----------------------------//     // RootFinder method overrides //     //-----------------------------//     /**      * Do the secant iteration procedure.      * @param n the iteration count      */     protected void doIterationProcedure(int n)     {         if (n == 1) return;     // already initialized         // Use the latest two points.         xnm1 = xn;     // x[n-1]    = x[n]         xn   = xnp1;   // x[n]      = x[n+1]         fnm1 = fn;     // f(x[n-1]) = f(x[n])         fn   = fnp1;   // f(x[n])   = f(x[n+1])     }     /**      * Compute the next position of x[n+1].      */     protected void computeNextPosition()     {         prevXnp1 = xnp1;         xnp1     = xn - fn*(xnm1 - xn)/(fnm1 - fn);         fnp1     = function.at(xnp1);     }     /**      * Check the position of x[n+1].      * @throws PositionUnchangedException      */     protected void checkPosition()         throws RootFinder.PositionUnchangedException     {         if (xnp1 == prevXnp1) {             throw new RootFinder.PositionUnchangedException();         }     }     /**      * Indicate whether or not the algorithm has converged.      * @return true if converged, else false      */     protected boolean hasConverged()     {         return Math.abs(fnp1) < TOLERANCE;     } } 

Program 5 C4 instantiates a SecantRootFinder object. Screen 5-4 shows the first two iterations of the interactive version of the program. This version requires you to set the values of x and x ₁ by clicking the mouse on their positions .

Screen 5-4. The first two iterations of the secant algorithm applied to the function f ( x ) = x ² - 4. The user sets the initial values of x and x ₁ with the mouse. At each iteration n, the two vertical lines mark the positions of x _{n - 1} and x _n . These screen shots are from the interactive version of Program 5 C4.

The noninteractive version of Program 5 C4 shows that, if we pick good starting values x and x ₁ , the secant algorithm can converge quickly. See Listing 5-4b.

Listing 5-4b The noninteractive version of Program 5 C4 applies the secant algorithm applied to the function f ( x ) = x ² - 4 with the initial values x = 0.3625 and x ₁ = 1.3625001.

 package numbercruncher.program5_4; import numbercruncher.mathutils.Function; import numbercruncher.mathutils.SecantRootFinder; import numbercruncher.mathutils.AlignRight; import numbercruncher.rootutils.RootFunctions; /**  * PROGRAM 5C4: Secant Algorithm  *  * Demonstrate the Secant Algorithm on a function.  */ public class SecantAlgorithm {     /**      * Main program.      * @param args the array of runtime arguments      */     public static void main(String args[])     {         try {             SecantRootFinder finder =                 new SecantRootFinder(RootFunctions.function("x^2 - 4"),                                                0.3625f, 1.3625001f);             AlignRight ar = new AlignRight();             ar.print("n", 2);             ar.print("x[n-1]", 10); ar.print("f(x[n-1])", 12);             ar.print("x[n]", 10); ar.print("f(x[n])", 13);             ar.print("x[n+1]", 10); ar.print("f(x[n+1])", 14);             ar.underline();             // Loop until convergence or failure.             boolean converged;             do {                 converged = finder.step();                 ar.print(finder.getIterationCount(), 2);                 ar.print(finder.getXnm1(), 10);                 ar.print(finder.getFnm1(), 12);                 ar.print(finder.getXn(), 10);                 ar.print(finder.getFn(), 13);                 ar.print(finder.getXnp1(), 10);                 ar.print(finder.getFnp1(), 14);                 ar.println();             } while (!converged);             System.out.println("\nSuccess! Root = " +                                finder.getXnp1());         }         catch(Exception ex) {             System.out.println("***** Error: " + ex);         }     } } 

Output:

 n    x[n-1]   f(x[n-1])      x[n]      f(x[n])    x[n+1]     f(x[n+1]) -----------------------------------------------------------------------  1    0.3625  -3.8685937 1.3625001   -2.1435935 2.6051629     2.7868733  2 1.3625001  -2.1435935 2.6051629    2.7868733 1.9027661   -0.37948108  3 2.6051629   2.7868733 1.9027661  -0.37948108  1.986947   -0.05204177  4 1.9027661 -0.37948108  1.986947  -0.05204177 2.0003262  0.0013046265  5  1.986947 -0.05204177 2.0003262 0.0013046265 1.9999989 -4.2915344E-6 Success! Root = 1.9999989 

---

Top