5.5 The Improved Regula Falsi Algorithm
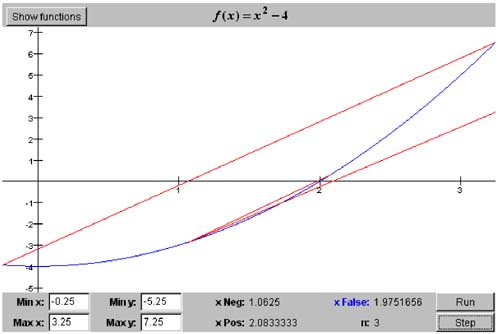
5.5 The Improved Regula Falsi Algorithm We can greatly improve the regula falsi algorithm with a simple trick. At the end of each iteration, if the sign of f ( x false ) did not change from the previous iteration (or if this is the first iteration), we decrease the slope of the secant. We do this by halving the height of the secant 's endpoint at the end of the interval that is not going to move. This trick also encourages the algorithm to approach a root from both sides. Class ImprovedRegulaFalsiRootFinder will implement the improved regula falsi algorithm. Program 5 C3 instantiates an object of this class. Screen 5-3 is a screen shot of the interactive version of the program. It shows the first three iterations for the function f ( x ) = x 2 - 4 in the initial interval [-0.25, 3.25]. For clarity, the program doesn't draw the vertical line that marks each position of x false . Notice that, in the second iteration, x false is to the right of the root. Screen 5-3. The first three iterations of the improved regula falsi algorithm applied to the function f ( x ) = x 2 - 4 in the initial interval [-0.25, 3.25]. This screen shot is from the interactive version of Program 5 C3. Listing 5-3a shows class ImprovedRegulaFalsiRootFinder. Since the algorithm is an improvement of the original regula falsi algorithm, the class simply extends class RegulaFalsiRootFinder. It overrides methods doIterationProcedure() and computeNextPosition() in order to decrease the secant slope when appropriate. Listing 5-3a The class that implements the improved regula falsi algorithm. package numbercruncher.mathutils; /** * The root finder class that implements the * improved regula falsi algorithm. */ public class ImprovedRegulaFalsiRootFinder extends RegulaFalsiRootFinder { /** previous f(xFalse) value */ private float prevFFalse; private boolean decreasePos = false; private boolean decreaseNeg = false; /** * Constructor. * @param function the functions whose roots to find * @param xMin the initial x-value where the function is negative * @param xMax the initial x-value where the function is positive * @throws RootFinder.InvalidIntervalException */ public ImprovedRegulaFalsiRootFinder(Function function, float xMin, float xMax) throws RootFinder.InvalidIntervalException { super(function, xMin, xMax); } //----------------------------------------// // Override RegulaFalsiRootFinder methods // //----------------------------------------// /** * Do the improved regula falsi iteration procedure. * @param n the iteration count */ protected void doIterationProcedure(int n) { super.doIterationProcedure(n); // Decrease the slope of the secant? if (decreasePos) fPos /= 2; if (decreaseNeg) fNeg /= 2; } /** * Compute the next position of xFalse. */ protected void computeNextPosition() { prevXFalse = xFalse; prevFFalse = fFalse; xFalse = xPos - fPos*(xNeg - xPos)/(fNeg - fPos); fFalse = function.at(xFalse); decreasePos = decreaseNeg = false; // If there was no sign change in f(xFalse), // or if this is the first iteration step, // then decrease the slope of the secant. if (Float.isNaN(prevFFalse) (prevFFalse*fFalse > 0)) { if (fFalse < 0) decreasePos = true; else decreaseNeg = true; } } } The noninteractive version of Program 5 C3 shows that, for the same function f ( x ) = x 2 - 4 and the same initial interval [-0.25, 3.25], the improved regula falsi algorithm has the best convergence rate so far. See Listing 5-3b. Listing 5-3b The noninteractive version of Program 5 C3 applies the improved regula falsi algorithm applied to the function f ( x ) = x 2 - 4 in the initial interval [-0.25, 3.25]. package numbercruncher.program5_3; import numbercruncher.mathutils.Function; import numbercruncher.mathutils.ImprovedRegulaFalsiRootFinder; import numbercruncher.mathutils.AlignRight; import numbercruncher.rootutils.RootFunctions; /** * PROGRAM 5C3: Improved Regula Falsi Algorithm * * Demonstrate the Improved Regula Falsi Algorithm on a function. */ public class ImprovedRegulaFalsiAlgorithm { /** * Main program. * @param args the array of runtime arguments */ public static void main(String args[]) { try { ImprovedRegulaFalsiRootFinder finder = new ImprovedRegulaFalsiRootFinder(RootFunctions.function("x^2 - 4"), -0.25f, 3.25f); AlignRight ar = new AlignRight(); ar.print("n", 2); ar.print("xNeg", 10); ar.print("f(xNeg)", 13); ar.print("xFalse", 10); ar.print("f(xFalse)", 13); ar.print("xPos", 10); ar.print("f(xPos)", 13); ar.underline(); // Loop until convergence or failure. boolean converged; do { converged = finder.step(); ar.print(finder.getIterationCount(), 2); ar.print(finder.getXNeg(), 10); ar.print(finder.getFNeg(), 13); ar.print(finder.getXFalse(), 10); ar.print(finder.getFFalse(), 13); ar.print(finder.getXPos(), 10); ar.print(finder.getFPos(), 13); ar.println(); } while (!converged); System.out.println("\nSuccess! Root = " + finder.getXFalse()); } catch(Exception ex) { System.out.println("***** Error: " + ex); } } } Output: n xNeg f(xNeg) xFalse f(xFalse) xPos f(xPos) ----------------------------------------------------------------------- 1 -0.25 -3.9375 1.0625 -2.8710938 3.25 6.5625 2 1.0625 -2.8710938 2.0833335 0.34027863 3.25 3.28125 3 1.0625 -2.8710938 1.9751655 -0.098721266 2.0833335 0.34027863 4 1.9751655 -0.098721266 1.99949 -0.002039671 2.0833335 0.34027863 5 1.99949 -0.002039671 2.0004833 0.0019330978 2.0833335 0.17013931 6 1.99949 -0.002039671 2.0 0.0 2.0004833 0.0019330978 Success! Root = 2.0 |
| |
| Top |
EAN: 2147483647
Pages: 141