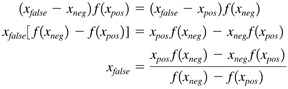5.4 The Regula Falsi Algorithm

	Java Number Cruncher: The Java Programmer's Guide to Numerical Computing By Ronald Mak
	Table of Contents

	Chapter 5. Finding Roots

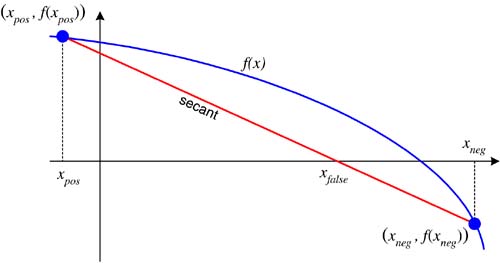
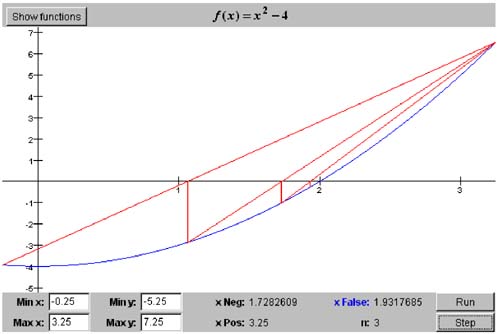
Obviously, a root-finding algorithm would converge faster if somehow the approximations were to get closer to the root faster. The algorithm of regula falsi (Latin for false position ) attempts to do just that with a smarter algorithm for generating the approximations (false positions ). We'll implement this algorithm in class RegulaFalsiRootFinder.

The basic idea is not hard to explain. Like the bisection algorithm, it is a bracketing algorithm that begins with an initial interval containing the root, and each iteration shrinks the interval to trap the root. For each iteration, we have x _neg and x _pos , the endpoints of interval, and we draw the secant (a line connecting two points on a curve) from the point ( x _neg , f ( x _neg )) to the point ( x _pos , f ( x _pos )). Then the new position x _false is where the secant crosses the x axis. See Figure 5-1.

Figure 5-1. A secant line for the function f ( x ) in the interval [ x _pos , x _neg ], where f ( x _pos ) > 0 and f ( x _neg ) < 0.

graphics/05fig01.jpg

We can compute the value of x _false using similar triangles . Because

we can cross-multiply and solve for x _false :

graphics/05equ07.gif

To simplify the right-hand side, we break apart the fraction, add and subtract x _pos , and manipulate the terms inside the square brackets:

graphics/05equ08.gif

The iteration procedure for the regula falsi algorithm is similar to that for the bisection algorithm. If f ( x _false ) < 0, then the root must be in the x _pos half of the interval, so the algorithm sets x _neg to x _false for the next iteration. On the other hand, if f ( x _false ) > 0, then the root must be in the x _neg half of the interval, so the algorithm sets x _pos to x _false for the next iteration. If f ( x _false ) is 0, or sufficiently close to 0, then the algorithm stops, and the final value of x _false is the root it managed to trap.

Screen 5-2 is a screen shot of the interactive version of Program 5 C2, which instantiates a RegulaFalsiRootFinder object. Screen 5-2 shows the first three iterations of the regula falsi algorithm applied to the function f ( x ) = x ² - 4 in the initial interval [-0.25, 3.25]. Notice that the algorithm tends to converge toward the root from one side only.

Screen 5-2. The first three iterations of the regula falsi algorithm applied to the function f ( x ) = x ² - 4 in the initial interval [-0.25, 3.25]. The three secant lines (and the short vertical lines marking the positions of x _false ) are superimposed on each other. This screen shot is from the interactive version of Program 5 C2.

graphics/05scr02.jpg

Listing 5-2a shows the class RegulaFalsiRootFinder , which implements this algorithm. It is very similar to class BisectionRootFinder.

Listing 5-2a The class that implements the regula falsi algorithm.

 package numbercruncher.mathutils; /**  * The root finder class that implements the regula falsi algorithm.  */ public class RegulaFalsiRootFinder extends RootFinder {     private static final int   MAX_ITERS = 50;     private static final float TOLERANCE = 100*Epsilon.floatValue();     /** x-negative value */        protected float xNeg;     /** x-false value */           protected float xFalse = Float.NaN;     /** x-positive value */        protected float xPos;     /** previous x-false value */  protected float prevXFalse;     /** f(xNeg) */                 protected float fNeg;     /** f(xFalse) */               protected float fFalse = Float.NaN;     /** f(xPos) */                 protected float fPos;     /**      * Constructor.      * @param function the functions whose roots to find      * @param xMin the initial x-value where the function is negative      * @param xMax the initial x-value where the function is positive      * @throws RootFinder.InvalidIntervalException      */     public RegulaFalsiRootFinder(Function function,                                  float xMin, float xMax)         throws RootFinder.InvalidIntervalException     {         super(function, MAX_ITERS);         checkInterval(xMin, xMax);         float yMin = function.at(xMin);         float yMax = function.at(xMax);         // Initialize xNeg, fNeg, xPos, and fPos.         if (yMin < 0) {             xNeg = xMin; xPos = xMax;             fNeg = yMin; fPos = yMax;         }         else {             xNeg = xMax; xPos = xMin;             fNeg = yMax; fPos = yMin;         }     }     //---------//     // Getters //     //---------//     /**      * Return the current value of x-negative.      * @return the value      */     public float getXNeg() { return xNeg; }     /**      * Return the current value of x-false.      * @return the value      */     public float getXFalse() { return xFalse; }     /**      * Return the current value of x-positive.      * @return the value      */     public float getXPos() { return xPos; }     /**      * Return the current value of f(x-negative).      * @return the value      */     public float getFNeg() { return fNeg; }     /**      * Return the current value of f(x-false).      * @return the value      */     public float getFFalse() { return fFalse; }     /**      * Return the current value of f(x-positive).      * @return the value      */     public float getFPos() { return fPos; }     //----------------------------//     // RootFinder method overrides //     //----------------------------//     /**      * Do the regula falsi iteration procedure.      * @param n the iteration count      */     protected void doIterationProcedure(int n)     {         if (n == 1) return;     // already initialized         if (fFalse < 0) {             xNeg = xFalse;      // the root is in the xPos side             fNeg = fFalse;         }         else {             xPos = xFalse;      // the root is in the xNeg side             fPos = fFalse;         }     }     /**      * Compute the next position of x-false.      */     protected void computeNextPosition()     {         prevXFalse = xFalse;         xFalse     = xPos - fPos*(xNeg - xPos)/(fNeg - fPos);         fFalse     = function.at(xFalse);     }     /**      * Check the position of x-false.      * @throws PositionUnchangedException      */     protected void checkPosition()         throws RootFinder.PositionUnchangedException     {         if (xFalse == prevXFalse) {             throw new RootFinder.PositionUnchangedException();         }     }     /**      * Indicate whether or not the algorithm has converged.      * @return true if converged, else false      */     protected boolean hasConverged()     {         return Math.abs(fFalse) < TOLERANCE;     } }

The noninteractive version of Program 5 C2 instantiates a RegulaFalsiRootFinder object, and it shows that, for the same function f ( x ) = x ² - 4 and the same initial interval [-0.25, 3.25], the regula falsi algorithm converges faster than the bisection algorithm. See Listing 5-2b.

Listing 5-2b The noninteractive version of Program 5 C2 applies the regula falsi algorithm applied to the function f ( x ) = x ² - 4 in the initial interval [-0.25, 3.25].

 package numbercruncher.program5_2; import numbercruncher.mathutils.Function; import numbercruncher.mathutils.RegulaFalsiRootFinder; import numbercruncher.mathutils.AlignRight; import numbercruncher.rootutils.RootFunctions; /**  * PROGRAM 5C2: Regula Falsi Algorithm  *  * Demonstrate the Regula Falsi Algorithm on a function.  */ public class RegulaFalsiAlgorithm {     /**      * Main program.      * @param args the array of runtime arguments      */     public static void main(String args[])     {         try {             RegulaFalsiRootFinder finder =                 new RegulaFalsiRootFinder(RootFunctions.function("x^2 - 4"),                                                -0.25f, 3.25f);             AlignRight ar = new AlignRight();             ar.print("n", 2);             ar.print("xNeg", 11); ar.print("f(xNeg)", 15);             ar.print("xFalse", 11); ar.print("f(xFalse)", 15);             ar.print("xPos", 6); ar.print("f(xPos)", 9);             ar.underline();             // Loop until convergence or failure.             boolean converged;             do {                 converged = finder.step();                 ar.print(finder.getIterationCount(), 2);                 ar.print(finder.getXNeg(), 11);                 ar.print(finder.getFNeg(), 15);                 ar.print(finder.getXFalse(), 11);                 ar.print(finder.getFFalse(), 15);                 ar.print(finder.getXPos(), 6);                 ar.print(finder.getFPos(), 9);                 ar.println();             } while (!converged);             System.out.println("\nSuccess! Root = " +                                finder.getXFalse());         }         catch(Exception ex) {             System.out.println("***** Error: " + ex);         }     } }

Output:

 n       xNeg        f(xNeg)     xFalse      f(xFalse)  xPos  f(xPos) ---------------------------------------------------------------------  1      -0.25        -3.9375     1.0625     -2.8710938  3.25   6.5625  2     1.0625     -2.8710938  1.7282609     -1.0131145  3.25   6.5625  3  1.7282609     -1.0131145  1.9317685    -0.26827025  3.25   6.5625  4  1.9317685    -0.26827025  1.9835405    -0.06556702  3.25   6.5625  5  1.9835405    -0.06556702  1.9960688   -0.015709162  3.25   6.5625  6  1.9960688   -0.015709162  1.9990634  -0.0037455559  3.25   6.5625  7  1.9990634  -0.0037455559   1.999777   -8.921623E-4  3.25   6.5625  8   1.999777   -8.921623E-4  1.9999468  -2.1266937E-4  3.25   6.5625  9  1.9999468  -2.1266937E-4  1.9999874   -5.054474E-5  3.25   6.5625 10  1.9999874   -5.054474E-5   1.999997  -1.1920929E-5  3.25   6.5625 11   1.999997  -1.1920929E-5  1.9999992    -3.33786E-6  3.25   6.5625 Success! Root = 1.9999992

The output shows that the value of x _pos never changed the algorithm converged to the root from one side only.

Top

Figure 5-1. A secant line for the function f ( x ) in the interval [ x pos , x neg ], where f ( x pos ) > 0 and f ( x neg ) < 0.

Listing 5-2a The class that implements the regula falsi algorithm.

Listing 5-2b The noninteractive version of Program 5 C2 applies the regula falsi algorithm applied to the function f ( x ) = x 2 - 4 in the initial interval [-0.25, 3.25].

Figure 5-1. A secant line for the function f ( x ) in the interval [ x _pos , x _neg ], where f ( x _pos ) > 0 and f ( x _neg ) < 0.

Listing 5-2b The noninteractive version of Program 5 C2 applies the regula falsi algorithm applied to the function f ( x ) = x ² - 4 in the initial interval [-0.25, 3.25].