5.3 The Bisection Algorithm
5.3 The Bisection Algorithm We begin with the simplest algorithm. Suppose we have a continuous function (its values have no breaks) over the interval between x neg and x pos . If f ( x neg ) < 0 and f ( x pos ) > 0, then we know that f ( x ) must cross the x axis an odd number of times (and hence it must have at least one root) in the interval. [1] Note that x neg itself is not necessarily negative, nor is x pos itself necessarily positive, and that either x neg < x pos or x neg > x pos . We can use the bisection algorithm, which reminds us of a binary search for an element of a sorted array of numbers .
The algorithm starts with the entire interval, and for each iteration, it performs the following actions:
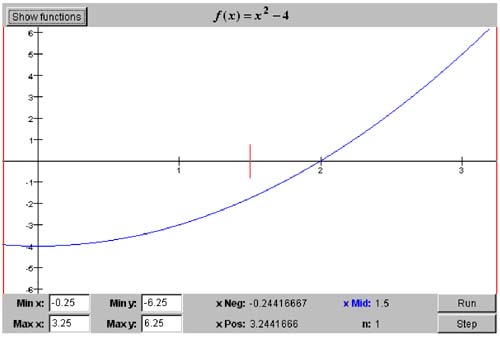
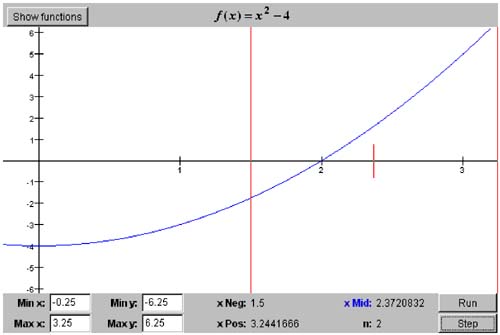
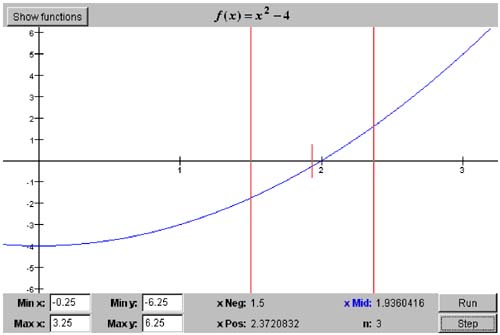
Even though we described these actions in the specific terms of the bisection algorithm, they apply in general to all the root-finding algorithms covered in this chapter. Therefore, can build a framework for these algorithms by creating an abstract RootFinder base class in package numbercruncher.mathutils. From this class, we can derive subclasses that implement the algorithms. Listing 5-0d shows this base class. Listing 5-0d The abstract base class for the subclasses that implement root-finding algorithms. package numbercruncher.mathutils; /** * Abstract base class for the root finder classes. */ public abstract class RootFinder { /** the function whose roots to find */ protected Function function; /** iteration counter */ private int n; /** maximum number of iterations */ private int maxIters; /** * Constructor. * @param function the function whose roots to find * @param maxIters the maximum number of iterations */ public RootFinder(Function function, int maxIters) { this.function = function; this.maxIters = maxIters; } /** * Check the interval. * @param xMin x-coordinate of the left of the interval * @param xMax x-coordinate of the right end of the interval * @throws InvalidIntervalException */ public void checkInterval(float x1, float x2) throws InvalidIntervalException { float y1 = function.at(x1); float y2 = function.at(x2); // The interval is invalid if y1 and y2 have the same signs. if (y1*y2 > 0) throw new InvalidIntervalException(); } /** * Return the iteration count. * @return the count */ public int getIterationCount() { return n; } /** * Perform one iteration step. * @return true if the algorithm converged, else false * @throws IterationCountExceededException * @throws PositionUnchangedException */ public boolean step() throws IterationCountExceededException, PositionUnchangedException { checkIterationCount(); doIterationProcedure(n); computeNextPosition(); checkPosition(); return hasConverged(); } /** * Check the iteration count to see if it has exeeded * the maximum number of iterations. * @throws IterationCountExceededException */ protected void checkIterationCount() throws IterationCountExceededException { if (++n > maxIters) { throw new IterationCountExceededException(); } } /** * Reset. */ protected void reset() { n = 0; } //------------------// // Subclass methods // //------------------// /** * Do the iteration procedure. * @param n the iteration count */ protected abstract void doIterationProcedure(int n); /** * Compute the next position of x. */ protected abstract void computeNextPosition(); /** * Check the position of x. * @throws PositionUnchangedException */ protected abstract void checkPosition() throws PositionUnchangedException; /** * Indicate whether or not the algorithm has converged. * @return true if converged, else false */ protected abstract boolean hasConverged(); //------------------------// // Root finder exceptions // //------------------------// /** * Invalid interval exception. */ public class InvalidIntervalException extends java.lang.Exception {} /** * Iteration count exceeded exception. */ public class IterationCountExceededException extends java.lang.Exception {} /** * Position unchanged exception. */ public class PositionUnchangedException extends java.lang.Exception {} } The key method of the base class is step() , which performs one iteration step of the root-finding algorithm. It invokes methods to do the actions described on page 112, and returns true if the algorithm has converged, or false otherwise . Except for checkIterationCount() , all of these methods will be implemented by the subclasses. The base class also defines several exceptions, RootFinder.InvalidInterval Exception, RootFinder.IterationCountExceededException , and RootFinder. PositionUnchangedException. Certain methods throw these exceptions. Method check IterationCount() can throw RootFinder.IterationCountExceededException. The subclass implementation of checkPosition() can throw RootFinder.Position UnchangedException if necessary. Therefore, method step() , which invokes both methods, can also throw either of these two exceptions. Some of the algorithms, including the bisection algorithm, require that the function value have different signs at the two ends of the interval. The base class provides the handy method check Interval() to test an interval, and it can throw RootFinder.InvalidIntervalException. From the RootFinder base class, we can derive our first root-finding algorithm class, BisectionRootFinder. Like all the root-finding classes, it will be in the numbercruncher.mathutils package. See Listing 5-1a. Listing 5-1a The class that implements the bisection algorithm. package numbercruncher.mathutils; /** * The root finder class that implements the bisection algorithm. */ public class BisectionRootFinder extends RootFinder { private static final int MAX_ITERS = 50; private static final float TOLERANCE = 100*Epsilon.floatValue(); /** x-negative value */ private float xNeg; /** x-middle value */ private float xMid = Float.NaN; /** x-positive value */ private float xPos; /** previous x-middle value */ private float prevXMid; /** f(xNeg) */ private float fNeg; /** f(xMid) */ private float fMid; /** f(xPos) */ private float fPos; /** * Constructor. * @param function the functions whose roots to find * @param xMin the initial x-value where the function is negative * @param xMax the initial x-value where the function is positive * @throws RootFinder.InvalidIntervalException */ public BisectionRootFinder(Function function, float xMin, float xMax) throws RootFinder.InvalidIntervalException { super(function, MAX_ITERS); checkInterval(xMin, xMax); float yMin = function.at(xMin); float yMax = function.at(xMax); // Initialize xNeg, fNeg, xPos, and fPos. if (yMin < 0) { xNeg = xMin; xPos = xMax; fNeg = yMin; fPos = yMax; } else { xNeg = xMax; xPos = xMin; fNeg = yMax; fPos = yMin; } } //CCCCCCCCC// // Getters // //CCCCCCCCC// /** * Return the current value of x-negative. * @return the value */ public float getXNeg() { return xNeg; } /** * Return the current value of x-middle. * @return the value */ public float getXMid() { return xMid; } /** * Return the current value of x-positive. * @return the value */ public float getXPos() { return xPos; } /** * Return the current value of f(x-negative). * @return the value */ public float getFNeg() { return fNeg; } /** * Return the current value of f(x-middle). * @return the value */ public float getFMid() { return fMid; } /** * Return the current value of f(x-positive). * @return the value */ public float getFPos() { return fPos; } //-----------------------------// // RootFinder method overrides // //-----------------------------// /** * Do the bisection iteration procedure. * @param n the iteration count */ protected void doIterationProcedure(int n) { if (n == 1) return; // already initialized if (fMid < 0) { xNeg = xMid; // the root is in the xPos half fNeg = fMid; } else { xPos = xMid; // the root is in the xNeg half fPos = fMid; } } /** * Compute the next position of xMid. */ protected void computeNextPosition() { prevXMid = xMid; xMid = (xNeg + xPos)/2; fMid = function.at(xMid); } /** * Check the position of xMid. * @throws PositionUnchangedException */ protected void checkPosition() throws RootFinder.PositionUnchangedException { if (xMid == prevXMid) { throw new RootFinder.PositionUnchangedException(); } } /** * Indicate whether or not the algorithm has converged. * @return true if converged, else false */ protected boolean hasConverged() { return Math.abs(fMid) < TOLERANCE; } } As we can see, other than the constructor that initializes the instance variables and the getter methods for these variables , the class mostly implements the abstract methods of the RootFinder base class. Method doIterationProcedure() adjusts one or the other end of the interval, depending on whether the value of the function at x mid is positive or negative. The method makes no changes during the first iteration, since values passed into the constructor determine the initial interval. Method computeNextPosition() computes the next value of x mid by finding the current interval's midpoint. Method checkPosition() makes sure that this midpoint is still changing. Finally, method hasConverged() checks to see if the value of the function at x mid is "sufficiently close" to zero. For this algorithm and the others in this chapter, we chose 50 as the maximum number of iterations, and 100 as the tolerance for being close to zero, where is the machine epsilon value we computed at the end of Chapter 3. These two values are somewhat arbitrary?awe chose them after some experimentation. If we set the tolerance too low, we run the risk of an algorithm never reaching it. The maximum number of iterations prevents a failing algorithm from running away. Program 5 §C1 instantiates a BisectionRootFinder object to demonstrate the bisection algorithm on a Function object. But before we see its source listing and the output, let's look at an interactive GUI-based version of the program. [2] The interactive version allows you to select any of the functions listed in Table 5-1 that are named f. Screen 5-1 shows screen shots of the first three iterations of the bisection algorithm applied to f ( x ) = x 2 - 4, starting with the interval [-0.25, 3.25]. For each iteration, notice how either x neg or x pos changes, depending on whether the value of f ( x mid ) was positive or negative in the previous iteration. (The interactive program can automatically run through its iteration steps with a short pause at the end of each one, or you can manually single-step one iteration at a time. The screen shots in Screen 5-1 were made from the single-step mode.)
Screen 5-1. The first three iterations of the bisection algorithm applied to the function f ( x ) = x 2 - 4 in the initial interval [-0.25, 3.25]. The tall vertical lines mark the current ends of the interval, and the short vertical line marks the current value of x mid . These screen shots are from the interactive version of Program 5 §C1. Because of the ever-shrinking interval, the bisection algorithm is a bracketing algorithm. The noninteractive version of Program 5 §C1 prints out, for each iteration, the current values of x neg , f ( x neg ), x mid , f ( x mid ), x pos , and f ( x pos ). The values of x mid converge to the root trapped by x neg and x pos . The main() method simply loops until the algorithm either succeeds or fails. See Listing 5-1b. Listing 5-1b The noninteractive version of Program 5 §C1 applies the bisection algorithm to the function f ( x ) = x 2 - 4 in the initial interval [-0.25, 3.25]. package numbercruncher.program5_1; import numbercruncher.mathutils.Function; import numbercruncher.mathutils.BisectionRootFinder; import numbercruncher.mathutils.AlignRight; import numbercruncher.rootutils.RootFunctions; /** * PROGRAM 5C1: Bisection Algorithm * * Demonstrate the Bisection Algorithm on a function. */ public class BisectionAlgorithm { /** * Main program. * @param args the array of runtime arguments */ public static void main(String args[]) { try { BisectionRootFinder finder = new BisectionRootFinder(RootFunctions.function("x^2 - 4"), -0.25f, 3.25f); AlignRight ar = new AlignRight(); ar.print("n", 2); ar.print("xNeg", 10); ar.print("f(xNeg)", 14); ar.print("xMid", 10); ar.print("f(xMid)", 14); ar.print("xPos", 10); ar.print("f(xPos)", 13); ar.underline(); // Loop until convergence or failure. boolean converged; do { converged = finder.step(); ar.print(finder.getIterationCount(), 2); ar.print(finder.getXNeg(), 10); ar.print(finder.getFNeg(), 14); ar.print(finder.getXMid(), 10); ar.print(finder.getFMid(), 14); ar.print(finder.getXPos(), 10); ar.print(finder.getFPos(), 13); ar.println(); } while (!converged); System.out.println("\nSuccess! Root = " + finder.getXMid()); } catch(Exception ex) { System.out.println("***** Error: " + ex); } } } Output: n xNeg f(xNeg) xMid f(xMid) xPos f(xPos) ------------------------------------------------------------------------- 1 -0.25 -3.9375 1.5 -1.75 3.25 6.5625 2 1.5 -1.75 2.375 1.640625 3.25 6.5625 3 1.5 -1.75 1.9375 -0.24609375 2.375 1.640625 4 1.9375 -0.24609375 2.15625 0.64941406 2.375 1.640625 5 1.9375 -0.24609375 2.046875 0.18969727 2.15625 0.64941406 6 1.9375 -0.24609375 1.9921875 -0.031188965 2.046875 0.18969727 7 1.9921875 -0.031188965 2.0195312 0.07850647 2.046875 0.18969727 8 1.9921875 -0.031188965 2.0058594 0.023471832 2.0195312 0.07850647 9 1.9921875 -0.031188965 1.9990234 -0.0039052963 2.0058594 0.023471832 10 1.9990234 -0.0039052963 2.0024414 0.009771347 2.0058594 0.023471832 11 1.9990234 -0.0039052963 2.0007324 0.0029301643 2.0024414 0.009771347 12 1.9990234 -0.0039052963 1.9998779 -4.8828125E-4 2.0007324 0.0029301643 13 1.9998779 -4.8828125E-4 2.0003052 0.0012207031 2.0007324 0.0029301643 14 1.9998779 -4.8828125E-4 2.0000916 3.6621094E-4 2.0003052 0.0012207031 15 1.9998779 -4.8828125E-4 1.9999847 -6.1035156E-5 2.0000916 3.6621094E-4 16 1.9999847 -6.1035156E-5 2.0000381 1.5258789E-4 2.0000916 3.6621094E-4 17 1.9999847 -6.1035156E-5 2.0000114 4.5776367E-5 2.0000381 1.5258789E-4 18 1.9999847 -6.1035156E-5 1.9999981 -7.6293945E-6 2.0000114 4.5776367E-5 19 1.9999981 -7.6293945E-6 2.0000048 1.9073486E-5 2.0000114 4.5776367E-5 20 1.9999981 -7.6293945E-6 2.0000014 5.722046E-6 2.0000048 1.9073486E-5 Success! Root = 2.0000014 The bisection algorithm is very easy to program, but how well does it work? Much more like the tortoise than the hare, if there is at least one real root in an interval, the algorithm will eventually find one of them. Of course, how fast the algorithm converges depends on the function and on the initial interval. Also, if there is more than one real root, which one the algorithm will converge to depends on the initial interval. The bisection algorithm uses a very simple formula to determine the next approximation of the root: the midpoint of the current interval. Thus, its convergence rate is linear?athe absolute error between the latest value of x mid and the root is decreased at best by one half of the size of the current interval per iteration. |
| |
| Top |
EAN: 2147483647
Pages: 141